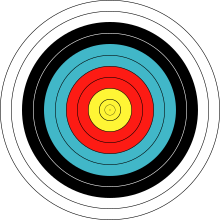
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius.
In geometry, a polygon is a plane figure made up of line segments connected to form a closed polygonal chain.

In geometry, a hexagon is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.

In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant concyclic points defined from the triangle. These nine points are:

In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle.

In geometry, a decagon is a ten-sided polygon or 10-gon. The total sum of the interior angles of a simple decagon is 1440°.
In Euclidean geometry, a regular polygon is a polygon that is direct equiangular and equilateral. Regular polygons may be either convex, star or skew. In the limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon, if the edge length is fixed.

In geometry, a set of points are said to be concyclic if they lie on a common circle. A polygon whose vertices are concyclic is called a cyclic polygon, and the circle is called its circumscribing circle or circumcircle. All concyclic points are equidistant from the center of the circle.
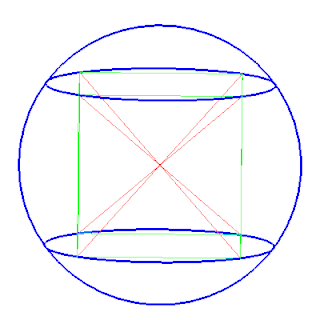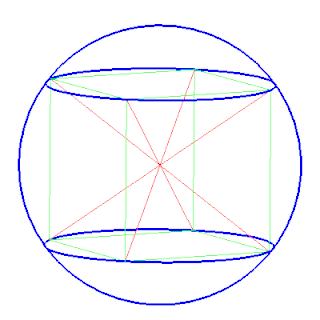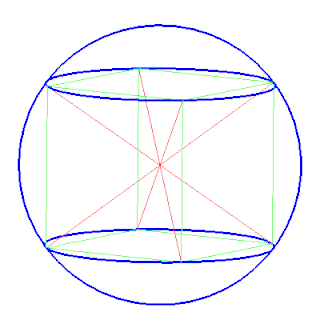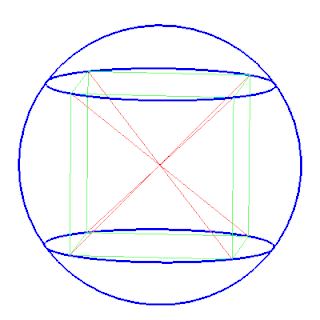
In geometry, a circumscribed sphere of a polyhedron is a sphere that contains the polyhedron and touches each of the polyhedron's vertices. The word circumsphere is sometimes used to mean the same thing, by analogy with the term circumcircle. As in the case of two-dimensional circumscribed circles (circumcircles), the radius of a sphere circumscribed around a polyhedron P is called the circumradius of P, and the center point of this sphere is called the circumcenter of P.
In geometry, the circumscribed circle or circumcircle of a triangle is a circle that passes through all three vertices. The center of this circle is called the circumcenter of the triangle, and its radius is called the circumradius. The circumcenter is the point of intersection between the three perpendicular bisectors of the triangle's sides, and is a triangle center.

In geometry, a pencil is a family of geometric objects with a common property, for example the set of lines that pass through a given point in a plane, or the set of circles that pass through two given points in a plane.

In geometry, an inscribed planar shape or solid is one that is enclosed by and "fits snugly" inside another geometric shape or solid. To say that "figure F is inscribed in figure G" means precisely the same thing as "figure G is circumscribed about figure F". A circle or ellipse inscribed in a convex polygon is tangent to every side or face of the outer figure. A polygon inscribed in a circle, ellipse, or polygon has each vertex on the outer figure; if the outer figure is a polygon or polyhedron, there must be a vertex of the inscribed polygon or polyhedron on each side of the outer figure. An inscribed figure is not necessarily unique in orientation; this can easily be seen, for example, when the given outer figure is a circle, in which case a rotation of an inscribed figure gives another inscribed figure that is congruent to the original one.

In geometry, a centre or center of an object is a point in some sense in the middle of the object. According to the specific definition of centre taken into consideration, an object might have no centre. If geometry is regarded as the study of isometry groups, then a centre is a fixed point of all the isometries that move the object onto itself.
Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. Geometry is one of the oldest mathematical sciences.

In geometry, a bicentric polygon is a tangential polygon which is also cyclic — that is, inscribed in an outer circle that passes through each vertex of the polygon. All triangles and all regular polygons are bicentric. On the other hand, a rectangle with unequal sides is not bicentric, because no circle can be tangent to all four sides.
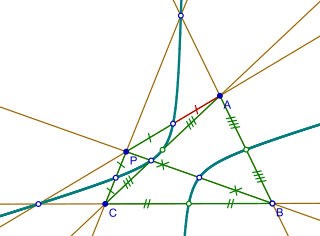
In Euclidean geometry with triangle △ABC, the nine-point hyperbola is an instance of the nine-point conic described by American mathematician Maxime Bôcher in 1892. The celebrated nine-point circle is a separate instance of Bôcher's conic:
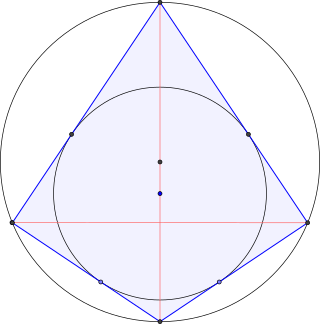
In Euclidean geometry, a right kite is a kite that can be inscribed in a circle. That is, it is a kite with a circumcircle. Thus the right kite is a convex quadrilateral and has two opposite right angles. If there are exactly two right angles, each must be between sides of different lengths. All right kites are bicentric quadrilaterals, since all kites have an incircle. One of the diagonals divides the right kite into two right triangles and is also a diameter of the circumcircle.

In mathematics and particularly in elementary geometry, a circumgon is a geometric figure which circumscribes some circle, in the sense that it is the union of the outer edges of non-overlapping triangles each of which has a vertex at the center of the circle and opposite side on a line that is tangent to the circle. The limiting case in which part or all of the circumgon is a circular arc is permitted. A circumgonal region is the union of those triangular regions.

In mathematics, modern triangle geometry, or new triangle geometry, is the body of knowledge relating to the properties of a triangle discovered and developed roughly since the beginning of the last quarter of the nineteenth century. Triangles and their properties were the subject of investigation since at least the time of Euclid. In fact, Euclid's Elements contains description of the four special points – centroid, incenter, circumcenter and orthocenter - associated with a triangle. Even though Pascal and Ceva in the seventeenth century, Euler in the eighteenth century and Feuerbach in the nineteenth century and many other mathematicians had made important discoveries regarding the properties of the triangle, it was the publication in 1873 of a paper by Emile Lemoine (1840–1912) with the title "On a remarkable point of the triangle" that was considered to have, according to Nathan Altschiller-Court, "laid the foundations...of the modern geometry of the triangle as a whole." The American Mathematical Monthly, in which much of Lemoine's work is published, declared that "To none of these [geometers] more than Émile-Michel-Hyacinthe Lemoine is due the honor of starting this movement of modern triangle geometry". The publication of this paper caused a remarkable upsurge of interest in investigating the properties of the triangle during the last quarter of the nineteenth century and the early years of the twentieth century. A hundred-page article on triangle geometry in Klein's Encyclopedia of Mathematical Sciences published in 1914 bears witness to this upsurge of interest in triangle geometry.