Cosmological phase transition

Last updated

A cosmological phase transition is a physical process, whereby the overall state of matter changes together across the whole universe. The success of the Big Bang model led researchers to conjecture possible cosmological phase transitions taking place in the very early universe, at a time when it was much hotter and denser than today. [1] [2]

Contents

Any cosmological phase transition may have left signals which are observable today, even if it took place in the first moments after the Big Bang, when the universe was opaque to light. [3]

Cosmological first-order phase transitions

Phase transitions can be categorised by their order. Transitions which are first order proceed via bubble nucleation and release latent heat as the bubbles expand.

As the universe cooled after the hot Big Bang, such a phase transition would have released huge amounts of energy, both as heat and as the kinetic energy of growing bubbles. In a strongly first-order phase transition, the bubble walls may even grow at near the speed of light. [4] This, in turn, would lead to the production of a stochastic background of gravitational waves. [2] [5] Experiments such as NANOGrav and LISA may be sensitive to this signal. [6] [7]

Shown below are two snapshots from simulations of the evolution of a first-order cosmological phase transition. [8] Bubbles first nucleate, then expand and collide, eventually converting the universe from one phase to another.

Examples

The Standard Model of particle physics contains three fundamental forces, the electromagnetic force, the weak force and the strong force. Shortly after the Big Bang, the extremely high temperatures may have modified the character of these forces. While these three forces act differently today, it has been conjectured that they may have been unified in the high temperatures of the early universe. [9] [10]

Strong force phase transition

Today the strong force binds together quarks into protons and neutrons, in a phenomenon known as color confinement. However, at sufficiently high temperatures, protons and neutrons disassociate into free quarks. The strong force phase transition marks the end of the quark epoch. Studies of this transition based on lattice QCD have demonstrated that it would have taken place at a temperature of approximately 155 MeV, and would have been a smooth crossover transition. [11]

This conclusion assumes the simplest scenario at the time of the transition, and first- or second-order transitions are possible in the presence of a quark, baryon or neutrino chemical potential, or strong magnetic fields. [12] [13] [14] The different possible phase transition types are summarised by the strong force phase diagram.

Electroweak phase transition

The electroweak phase transition marks the moment when the Higgs mechanism first activated, ending the electroweak epoch. [15] [16] Just as for the strong force, lattice studies of the electroweak model have found the transition to be a smooth crossover, taking place at 159.5±1.5 GeV. [17]

Just as for the strong force, the conclusion that the transition is a crossover assumes the minimal scenario, and is modified by the presence of additional fields or particles. Particle physics models which account for dark matter or which lead to successful baryogenesis may predict a strongly first-order electroweak phase transition. [18]

Phase transitions beyond the Standard Model

If the three forces of the Standard Model are unified in a Grand Unified Theory, then there would have been a cosmological phase transition at even higher temperatures, corresponding to the moment when the forces first separated out. [9] [10] Cosmological phase transitions may also have taken place in a dark or hidden sector, amongst particles and fields that are only very weakly coupled to visible matter. [19]

See also

Related Research Articles

<span class="mw-page-title-main">Standard Model</span> Theory of forces and subatomic particles

The Standard Model of particle physics is the theory describing three of the four known fundamental forces in the universe and classifying all known elementary particles. It was developed in stages throughout the latter half of the 20th century, through the work of many scientists worldwide, with the current formulation being finalized in the mid-1970s upon experimental confirmation of the existence of quarks. Since then, proof of the top quark (1995), the tau neutrino (2000), and the Higgs boson (2012) have added further credence to the Standard Model. In addition, the Standard Model has predicted various properties of weak neutral currents and the W and Z bosons with great accuracy.

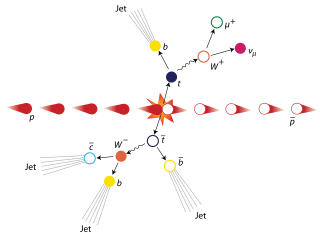
<span class="mw-page-title-main">Top quark</span> Type of quark

The top quark, sometimes also referred to as the truth quark, is the most massive of all observed elementary particles. It derives its mass from its coupling to the Higgs Boson. This coupling is very close to unity; in the Standard Model of particle physics, it is the largest (strongest) coupling at the scale of the weak interactions and above. The top quark was discovered in 1995 by the CDF and DØ experiments at Fermilab.

<span class="mw-page-title-main">Technicolor (physics)</span> Hypothetical model through which W and Z bosons acquire mass

Technicolor theories are models of physics beyond the Standard Model that address electroweak gauge symmetry breaking, the mechanism through which W and Z bosons acquire masses. Early technicolor theories were modelled on quantum chromodynamics (QCD), the "color" theory of the strong nuclear force, which inspired their name.

In physical cosmology, baryogenesis is the physical process that is hypothesized to have taken place during the early universe to produce baryonic asymmetry, i.e. the imbalance of matter (baryons) and antimatter (antibaryons) in the observed universe.

In physics, an infrared fixed point is a set of coupling constants, or other parameters, that evolve from initial values at very high energies to fixed stable values, usually predictable, at low energies. This usually involves the use of the renormalization group, which specifically details the way parameters in a physical system depend on the energy scale being probed.

In particle physics, the Peccei–Quinn theory is a well-known, long-standing proposal for the resolution of the strong CP problem formulated by Roberto Peccei and Helen Quinn in 1977. The theory introduces a new anomalous symmetry to the Standard Model along with a new scalar field which spontaneously breaks the symmetry at low energies, giving rise to an axion that suppresses the problematic CP violation. This model has long since been ruled out by experiments and has instead been replaced by similar invisible axion models which utilize the same mechanism to solve the strong CP problem.

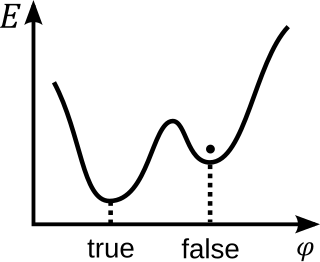
<span class="mw-page-title-main">False vacuum decay</span> Hypothetical vacuum, less stable than true vacuum

In quantum field theory, a false vacuum is a hypothetical vacuum that is relatively stable, but not in the most stable state possible. In this condition it is called metastable. It may last for a very long time in this state, but could eventually decay to the more stable one, an event known as false vacuum decay. The most common suggestion of how such a decay might happen in our universe is called bubble nucleation – if a small region of the universe by chance reached a more stable vacuum, this "bubble" would spread.

The Alternative models to the Standard Higgs Model are models which are considered by many particle physicists to solve some of the Higgs boson's existing problems. Two of the most currently researched models are quantum triviality, and Higgs hierarchy problem.

<span class="mw-page-title-main">Sphaleron</span> Solution to field equations in Standard Model particle physics

A sphaleron is a static (time-independent) solution to the electroweak field equations of the Standard Model of particle physics, and is involved in certain hypothetical processes that violate baryon and lepton numbers. Such processes cannot be represented by perturbative methods such as Feynman diagrams, and are therefore called non-perturbative. Geometrically, a sphaleron is a saddle point of the electroweak potential.

An exotic star is a hypothetical compact star composed of exotic matter, and balanced against gravitational collapse by degeneracy pressure or other quantum properties.

In physical cosmology, the electroweak epoch was the period in the evolution of the early universe when the temperature of the universe had fallen enough that the strong force separated from the electroweak interaction, but was high enough for electromagnetism and the weak interaction to remain merged into a single electroweak interaction above the critical temperature for electroweak symmetry breaking. Some cosmologists place the electroweak epoch at the start of the inflationary epoch, approximately 10−36 seconds after the Big Bang. Others place it at approximately 10−32 seconds after the Big Bang when the potential energy of the inflaton field that had driven the inflation of the universe during the inflationary epoch was released, filling the universe with a dense, hot quark–gluon plasma. Particle interactions in this phase were energetic enough to create large numbers of exotic particles, including W and Z bosons and Higgs bosons. As the universe expanded and cooled, interactions became less energetic and when the universe was about 10−12 seconds old, W and Z bosons ceased to be created at observable rates. The remaining W and Z bosons decayed quickly, and the weak interaction became a short-range force in the following quark epoch.

<span class="mw-page-title-main">Christopher T. Hill</span> American theoretical physicist

Christopher T. Hill is an American theoretical physicist at the Fermi National Accelerator Laboratory who did undergraduate work in physics at M.I.T., and graduate work at Caltech. Hill's Ph.D. thesis, "Higgs Scalars and the Nonleptonic Weak Interactions" (1977) contains one of the first detailed discussions of the two-Higgs-doublet model and its impact upon weak interactions.

<span class="mw-page-title-main">Primordial black hole</span> Hypothetical black hole formed soon after the Big Bang

In cosmology, primordial black holes (PBHs) are hypothetical black holes that formed soon after the Big Bang. In the inflationary era and early radiation-dominated universe, extremely dense pockets of subatomic matter may have been tightly packed to the point of gravitational collapse, creating primordial black holes without the supernova compression needed to make black holes today. Because the creation of primordial black holes would pre-date the first stars, they are not limited to the narrow mass range of stellar black holes.

In particle physics, W′ and Z′ bosons refer to hypothetical gauge bosons that arise from extensions of the electroweak symmetry of the Standard Model. They are named in analogy with the Standard Model W and Z bosons.

<span class="mw-page-title-main">Light front holography</span> Technique used to determine mass of hadrons

In strong interaction physics, light front holography or light front holographic QCD is an approximate version of the theory of quantum chromodynamics (QCD) which results from mapping the gauge theory of QCD to a higher-dimensional anti-de Sitter space (AdS) inspired by the AdS/CFT correspondence proposed for string theory. This procedure makes it possible to find analytic solutions in situations where strong coupling occurs, improving predictions of the masses of hadrons and their internal structure revealed by high-energy accelerator experiments. The most widely used approach to finding approximate solutions to the QCD equations, lattice QCD, has had many successful applications; however, it is a numerical approach formulated in Euclidean space rather than physical Minkowski space-time.

In theoretical physics, a mass generation mechanism is a theory that describes the origin of mass from the most fundamental laws of physics. Physicists have proposed a number of models that advocate different views of the origin of mass. The problem is complicated because the primary role of mass is to mediate gravitational interaction between bodies, and no theory of gravitational interaction reconciles with the currently popular Standard Model of particle physics.

The Kibble–Zurek mechanism (KZM) describes the non-equilibrium dynamics and the formation of topological defects in a system which is driven through a continuous phase transition at finite rate. It is named after Tom W. B. Kibble, who pioneered the study of domain structure formation through cosmological phase transitions in the early universe, and Wojciech H. Zurek, who related the number of defects it creates to the critical exponents of the transition and to its rate—to how quickly the critical point is traversed.

<span class="mw-page-title-main">Light-front quantization applications</span> Quantization procedure in quantum field theory

The light-front quantization of quantum field theories provides a useful alternative to ordinary equal-time quantization. In particular, it can lead to a relativistic description of bound systems in terms of quantum-mechanical wave functions. The quantization is based on the choice of light-front coordinates, where plays the role of time and the corresponding spatial coordinate is . Here, is the ordinary time, is a Cartesian coordinate, and is the speed of light. The other two Cartesian coordinates, and , are untouched and often called transverse or perpendicular, denoted by symbols of the type . The choice of the frame of reference where the time and -axis are defined can be left unspecified in an exactly soluble relativistic theory, but in practical calculations some choices may be more suitable than others. The basic formalism is discussed elsewhere.

George Michael Fuller is an American theoretical physicist, known for his research on nuclear astrophysics involving weak interactions, neutrino flavor-mixing, and quark matter, as well as the hypothetical nuclear matter.

References

  1. ↑ Guth, Alan H.; Tye, S.H. H. (1980). "Phase Transitions and Magnetic Monopole Production in the Very Early Universe". Phys. Rev. Lett. 44 (10): 631–635. Bibcode:1980PhRvL..44..631G. doi:10.1103/PhysRevLett.44.631. OSTI   1447535.
  2. 1 2 Witten, Edward (1984). "Cosmic Separation of Phases". Phys. Rev. D. 30: 272–285. doi:10.1016/0550-3213(81)90182-6.
  3. ↑ Kibble, T. W. B. (1980). "Some implications of a Cosmological Phase Transition". Phys. Rept. 67 (1): 183–199. Bibcode:1980PhR....67..183K. doi:10.1016/0370-1573(80)90091-5.
  4. ↑ Moore, Guy D.; Prokopec, Tomislav (1995). "Bubble wall velocity in a first order electroweak phase transition". Phys. Rev. Lett. 75 (5): 777–780. arXiv: hep-ph/9503296 . Bibcode:1995PhRvL..75..777M. doi:10.1103/PhysRevLett.75.777. PMID   10060116. S2CID   17239930.
  5. ↑ Hogan, C. J. (1986). "Gravitational radiation from cosmological phase transitions". Mon. Not. R. Astron. Soc. 218 (4): 629–636. doi: 10.1093/mnras/218.4.629 . Retrieved 9 August 2023.
  6. ↑ NANOGrav (2023). "The NANOGrav 15 yr Data Set: Search for Signals of New Physics". Astrophys. J. Lett. 951 (1): L11. arXiv: 2306.16219 . Bibcode:2023ApJ...951L..11A. doi: 10.3847/2041-8213/acdc91 .
  7. ↑ LISA Cosmology Working Group (2016). "Science with the space-based interferometer eLISA. II: Gravitational waves from cosmological phase transitions". JCAP. 04 (4): 001. arXiv: 1512.06239 . Bibcode:2016JCAP...04..001C. doi:10.1088/1475-7516/2016/04/001. S2CID   53333014.
  8. ↑ Weir, David (2018). "Gravitational waves from a first order electroweak phase transition: a brief review". Phil. Trans. Roy. Soc. Lond. A. 376: 20170126. doi: 10.1098/rsta.2017.0126 .
  9. 1 2 Georgi, H.; Glashow, S. L. (1974). "Unity of All Elementary Forces". Phys. Rev. Lett. 32: 438–441. doi:10.1103/PhysRevLett.32.438.
  10. 1 2 Weinberg, Steven (1974). "Gauge and Global Symmetries at High Temperature". Phys. Rev. D. 9 (12): 3357–3378. Bibcode:1974PhRvD...9.3357W. doi:10.1103/PhysRevD.9.3357.
  11. ↑ Aoki, Y.; Endrodi, G.; Fodor, Z.; Katz, S. D.; Szabo, K. K. (2006). "The order of the quantum chromodynamics transition predicted by the standard model of particle physics". Nature. 443 (7112): 675–678. arXiv: hep-lat/0611014 . Bibcode:2006Natur.443..675A. doi:10.1038/nature05120. PMID   17035999.
  12. ↑ Boeckel, Tillman; Schettler, Simon; Schaffner-Bielich, Jurgen (2011). "The Cosmological QCD Phase Transition Revisited". Prog. Part. Nucl. Phys. 66: 266–270. arXiv: 1012.3342 . doi:10.1016/j.ppnp.2011.01.017.
  13. ↑ Schwarz, Dominik J.; Stuke, Maik (2009). "Lepton asymmetry and the cosmic QCD transition". JCAP. 11: 025. arXiv: 0906.3434 . doi:10.1088/1475-7516/2009/11/025.
  14. ↑ Cao, Gaoging (2023). "First-order QCD transition in a primordial magnetic field". Phys. Rev. D. 107: 014021. arXiv: 2210.09794 . doi:10.1103/PhysRevD.107.014021.
  15. ↑ Guth, Alan H.; Weinberg, Eric J. (1980). "A Cosmological Lower Bound on the Higgs Boson Mass". Phys. Rev. Lett. 45 (14): 1131–1134. Bibcode:1980PhRvL..45.1131G. doi:10.1103/PhysRevLett.45.1131.
  16. ↑ Witten, Edward (1981). "Cosmological Consequences of a Light Higgs Boson". Nucl. Phys. B. 177 (3): 477–488. Bibcode:1981NuPhB.177..477W. doi:10.1016/0550-3213(81)90182-6.
  17. ↑ D'Onofrio, Michela; Rummukainen, Kari (2016). "Standard model cross-over on the lattice". Phys. Rev. D. 93 (2): 025003. arXiv: 1508.07161 . Bibcode:2016PhRvD..93b5003D. doi:10.1103/PhysRevD.93.025003. hdl: 10138/159845 . S2CID   119261776.
  18. ↑ Cline, James; Kainulainen, Kimmo (2013). "Electroweak baryogenesis and dark matter from a singlet Higgs". JCAP. 01: 012. arXiv: 1210.4196 . doi:10.1088/1475-7516/2013/01/012.
  19. ↑ Schwaller, Pedro (2015). "Gravitational waves from a dark phase transition". Phys. Rev. Lett. 115: 181101. doi: 10.1103/PhysRevLett.115.181101 .
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.