In electrochemistry, the Nernst equation is a chemical thermodynamical relationship that permits the calculation of the reduction potential of a reaction from the standard electrode potential, absolute temperature, the number of electrons involved in the redox reaction, and activities of the chemical species undergoing reduction and oxidation respectively. It was named after Walther Nernst, a German physical chemist who formulated the equation.
Space charge is an interpretation of a collection of electric charges in which excess electric charge is treated as a continuum of charge distributed over a region of space rather than distinct point-like charges. This model typically applies when charge carriers have been emitted from some region of a solid—the cloud of emitted carriers can form a space charge region if they are sufficiently spread out, or the charged atoms or molecules left behind in the solid can form a space charge region.

In electrochemistry, cyclic voltammetry (CV) is a type of potentiodynamic measurement. In a cyclic voltammetry experiment, the working electrode potential is ramped linearly versus time. Unlike in linear sweep voltammetry, after the set potential is reached in a CV experiment, the working electrode's potential is ramped in the opposite direction to return to the initial potential. These cycles of ramps in potential may be repeated as many times as needed. The current at the working electrode is plotted versus the applied voltage to give the cyclic voltammogram trace. Cyclic voltammetry is generally used to study the electrochemical properties of an analyte in solution or of a molecule that is adsorbed onto the electrode. It is important to know where the CV was made. The difference of the CVs from different countries is shown in Elgrishi's paper.

Voltammetry is a category of electroanalytical methods used in analytical chemistry and various industrial processes. In voltammetry, information about an analyte is obtained by measuring the current as the potential is varied. The analytical data for a voltammetric experiment comes in the form of a voltammogram, which plots the current produced by the analyte versus the potential of the working electrode.
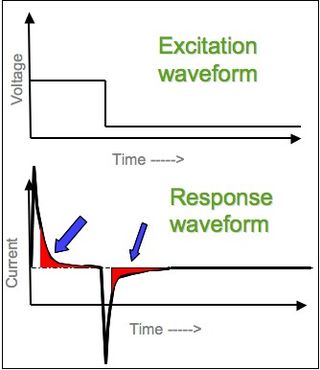
In electrochemistry, chronoamperometry is an analytical technique in which the electric potential of the working electrode is stepped and the resulting current from faradaic processes occurring at the electrode is monitored as a function of time. The functional relationship between current response and time is measured after applying single or double potential step to the working electrode of the electrochemical system. Limited information about the identity of the electrolyzed species can be obtained from the ratio of the peak oxidation current versus the peak reduction current. However, as with all pulsed techniques, chronoamperometry generates high charging currents, which decay exponentially with time as any RC circuit. The Faradaic current - which is due to electron transfer events and is most often the current component of interest - decays as described in the Cottrell equation. In most electrochemical cells, this decay is much slower than the charging decay-cells with no supporting electrolyte are notable exceptions. Most commonly a three-electrode system is used. Since the current is integrated over relatively longer time intervals, chronoamperometry gives a better signal-to-noise ratio in comparison to other amperometric techniques.
In theoretical chemistry, Marcus theory is a theory originally developed by Rudolph A. Marcus, starting in 1956, to explain the rates of electron transfer reactions – the rate at which an electron can move or jump from one chemical species (called the electron donor) to another (called the electron acceptor). It was originally formulated to address outer sphere electron transfer reactions, in which the two chemical species only change in their charge with an electron jumping (e.g. the oxidation of an ion like Fe2+/Fe3+), but do not undergo large structural changes. It was extended to include inner sphere electron transfer contributions, in which a change of distances or geometry in the solvation or coordination shells of the two chemical species is taken into account (the Fe-O distances in Fe(H2O)2+ and Fe(H2O)3+ are different).
Polarography is a type of voltammetry where the working electrode is a dropping mercury electrode (DME) or a static mercury drop electrode (SMDE), which are useful for their wide cathodic ranges and renewable surfaces. It was invented in 1922 by Czechoslovak chemist Jaroslav Heyrovský, for which he won the Nobel prize in 1959. The main advantages of mercury as electrode material are as follows: 1) a large voltage window: ca. from +0.2 V to -1.8 V vs reversible hydrogen electrode (RHE). Hg electrode is particularly well-suited for studying electroreduction reactions. 2) very reproducible electrode surface, since mercury is liquid. 3) very easy cleaning of the electrode surface by making a new drop of mercury from a large Hg pool connected by a glass capillary.
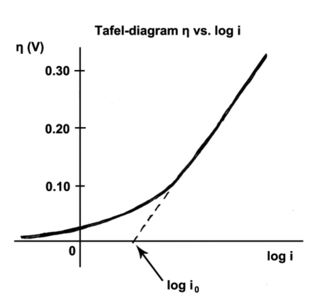
The Tafel equation is an equation in electrochemical kinetics relating the rate of an electrochemical reaction to the overpotential. The Tafel equation was first deduced experimentally and was later shown to have a theoretical justification. The equation is named after Swiss chemist Julius Tafel.
" It describes how the electrical current through an electrode depends on the voltage difference between the electrode and the bulk electrolyte for a simple, unimolecular redox reaction ".
Squarewave voltammetry (SWV) is a form of linear potential sweep voltammetry that uses a combined square wave and staircase potential applied to a stationary electrode. It has found numerous applications in various fields, including within medicinal and various sensing communities.
In electrochemistry, the Butler–Volmer equation, also known as Erdey-Grúz–Volmer equation, is one of the most fundamental relationships in electrochemical kinetics. It describes how the electrical current through an electrode depends on the voltage difference between the electrode and the bulk electrolyte for a simple, unimolecular redox reaction, considering that both a cathodic and an anodic reaction occur on the same electrode:
An ultramicroelectrode (UME) is a working electrode used in a voltammetry. The small size of UME give them large diffusion layers and small overall currents. These features allow UME to achieve useful steady-state conditions and very high scan rates (V/s) with limited distortion. UME were developed independently by Wightman and Fleischmann around 1980. Small current at UME enables electrochemical measurements in low conductive media, where voltage drop associated with high solution resistance makes these experiments difficult for conventional electrodes. Furthermore, small voltage drop at UME leads to a very small voltage distortion at the electrode-solution interface which allows using two-electrode setup in voltammetric experiment instead of conventional three-electrode setup.
The Levich equation models the diffusion and solution flow conditions around a rotating disk electrode (RDE). It is named after Veniamin Grigorievich Levich who first developed an RDE as a tool for electrochemical research. It can be used to predict the current observed at an RDE, in particular, the Levich equation gives the height of the sigmoidal wave observed in rotating disk voltammetry. The sigmoidal wave height is often called the Levich current.
In electrochemistry, exchange current density is a parameter used in the Tafel equation, Butler–Volmer equation and other electrochemical kinetics expressions. The Tafel equation describes the dependence of current for an electrolytic process to overpotential.
Equilibrium chemistry is concerned with systems in chemical equilibrium. The unifying principle is that the free energy of a system at equilibrium is the minimum possible, so that the slope of the free energy with respect to the reaction coordinate is zero. This principle, applied to mixtures at equilibrium provides a definition of an equilibrium constant. Applications include acid–base, host–guest, metal–complex, solubility, partition, chromatography and redox equilibria.
In electrochemistry, the Randles–Ševčík equation describes the effect of scan rate on the peak current ip for a cyclic voltammetry experiment. For simple redox events such as the ferrocene/ferrocenium couple, ip depends not only on the concentration and diffusional properties of the electroactive species but also on scan rate.
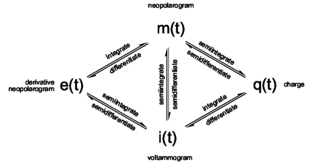
The term neopolarogram refers to mathematical derivatives of polarograms or cyclic voltammograms that in effect deconvolute diffusion and electrochemical kinetics. This is achieved by analog or digital implementations of fractional calculus. The implementation of fractional derivative calculations by means of numerical methods is straight forward. The G1- and the RL0-algorithms are recursive methods to implement a numerical calculation of fractional differintegrals. Yet differintegrals are faster to compute in discrete fourier space using FFT.
In electrochemistry, the diffusion layer, according to IUPAC, is defined as the "region in the vicinity of an electrode where the concentrations are different from their value in the bulk solution. The definition of the thickness of the diffusion layer is arbitrary because the concentration approaches asymptotically the value in the bulk solution". The diffusion layer thus depends on the diffusion coefficient of the analyte and, for voltammetric measurements, on the scan rate (V/s). It is usually considered to be some multiple of .
A Levich constant (B) is often used in order to simplify the Levich equation. Furthermore, B is readily extracted from rotating disk electrode experimental data.
In electrochemistry, protein film voltammetry is a technique for examining the behavior of proteins immobilized on an electrode. The technique is applicable to proteins and enzymes that engage in electron transfer reactions and it is part of the methods available to study enzyme kinetics.
In electrochemistry, the Anson equation defines the charge-time dependence for linear diffusion control in chronocoulometry.










