Couette flow

In fluid dynamics, Couette flow is the flow of a viscous fluid in the space between two surfaces, one of which is moving tangentially relative to the other. The relative motion of the surfaces imposes a shear stress on the fluid and induces flow. Depending on the definition of the term, there may also be an applied pressure gradient in the flow direction.

The Couette configuration models certain practical problems, like the Earth's mantle and atmosphere, ^[1] and flow in lightly loaded journal bearings. It is also employed in viscometry and to demonstrate approximations of reversibility. ^{[2] [3]}

It is named after Maurice Couette, a Professor of Physics at the French University of Angers in the late 19th century.

Planar Couette flow

Simple Couette configuration using two infinite flat plates.

Couette flow is frequently used in undergraduate physics and engineering courses to illustrate shear-driven fluid motion. A simple configuration corresponds to two infinite, parallel plates separated by a distance ${\displaystyle h}$; one plate translates with a constant relative velocity ${\displaystyle U}$ in its own plane. Neglecting pressure gradients, the Navier–Stokes equations simplify to

${\displaystyle {\frac {d^{2}u}{dy^{2}}}=0,}$

where ${\displaystyle y}$ is the spatial coordinate normal to the plates and ${\displaystyle u(y)}$ is the velocity field. This equation reflects the assumption that the flow is unidirectional — that is, only one of the three velocity components ${\displaystyle (u,v,w)}$ is non-trivial. If the lower plate corresponds to ${\displaystyle y=0}$, the boundary conditions are ${\displaystyle u(0)=0}$ and ${\displaystyle u(h)=U}$. The exact solution

${\displaystyle u(y)=U{\frac {y}{h}}}$

can be found by integrating twice and solving for the constants using the boundary conditions. A notable aspect of the flow is that shear stress is constant throughout the domain. In particular, the first derivative of the velocity, ${\displaystyle U/h}$, is constant. According to Newton's Law of Viscosity (Newtonian fluid), the shear stress is the product of this expression and the (constant) fluid viscosity.

Startup

Startup Couette flow

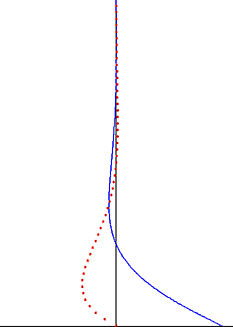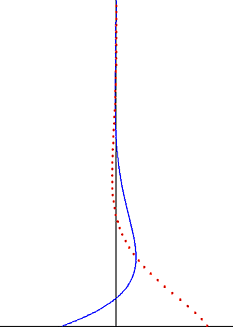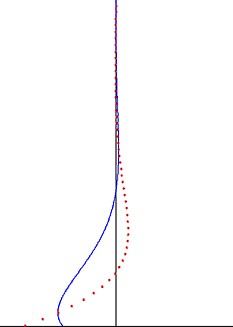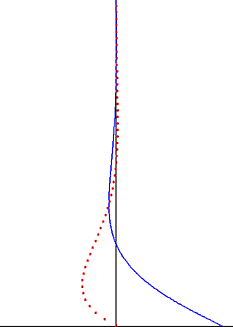
In reality, the Couette solution is not reached instantaneously. The "startup problem" describing the approach to steady state is given by

${\displaystyle {\frac {\partial u}{\partial t}}=\nu {\frac {\partial ^{2}u}{\partial y^{2}}}}$

subject to the initial condition

${\displaystyle u(y,0)=0,\quad 0<y<h,}$

and with the same boundary conditions as the steady flow:

${\displaystyle u(0,t)=0,\quad u(h,t)=U,\quad t>0.}$

The problem can be made homogeneous by subtracting the steady solution. Then, applying separation of variables leads to the solution: ^[4]

${\displaystyle u(y,t)=U{\frac {y}{h}}-{\frac {2U}{\pi }}\sum _{n=1}^{\infty }{\frac {1}{n}}e^{-n^{2}\pi ^{2}{\frac {\nu t}{h^{2}}}}\sin \left[n\pi \left(1-{\frac {y}{h}}\right)\right]}$.

The timescale describing relaxation to steady state is ${\displaystyle t\sim h^{2}/\nu }$, as illustrated in the figure. The time required to reach the steady state depends only on the spacing between the plates ${\displaystyle h}$ and the kinematic viscosity of the fluid, but not on ${\displaystyle U}$.

Planar flow with pressure gradient

A more general Couette flow includes a constant pressure gradient ${\displaystyle G=-dp/dx=\mathrm {constant} }$ in a direction parallel to the plates. The Navier–Stokes equations are

${\displaystyle {\frac {d^{2}u}{dy^{2}}}=-{\frac {G}{\mu }},}$

where ${\displaystyle \mu }$ is the dynamic viscosity. Integrating the above equation twice and applying the boundary conditions (same as in the case of Couette flow without pressure gradient) gives

${\displaystyle u(y)={\frac {G}{2\mu }}y\,(h-y)+U{\frac {y}{h}}.}$

The pressure gradient can be positive (adverse pressure gradient) or negative (favorable pressure gradient). In the limiting case of stationary plates (${\displaystyle U=0}$), the flow is referred to as Plane Poiseuille flow, and has a symmetric (with reference to the horizontal mid-plane) parabolic velocity profile. ^[5]

Compressible flow

Compressible Couette flow for ${\displaystyle \mathrm {M} =0}$

Compressible Couette flow for ${\displaystyle \mathrm {M} ^{2}\mathrm {Pr} =7.5}$

In incompressible flow, the velocity profile is linear because the fluid temperature is constant. When the upper and lower walls are maintained at different temperatures, the velocity profile is more complicated. However, it has an exact implicit solution as shown by C. R. Illingworth in 1950. ^[6]

Consider the plane Couette flow with lower wall at rest and the upper wall in motion with constant velocity ${\displaystyle U}$. Denote fluid properties at the lower wall with subscript ${\displaystyle w}$ and properties at the upper wall with subscript ${\displaystyle \infty }$. The properties and the pressure at the upper wall are prescribed and taken as reference quantities. Let ${\displaystyle l}$ be the distance between the two walls. The boundary conditions are

${\displaystyle u=0,\ v=0,\ h=h_{w}=c_{pw}T_{w}\ {\text{at}}\ y=0,}$

${\displaystyle u=U,\ v=0,\ h=h_{\infty }=c_{p\infty }T_{\infty },\ p=p_{\infty }\ {\text{at}}\ y=l}$

where ${\displaystyle h}$ is the specific enthalpy and ${\displaystyle c_{p}}$ is the specific heat. Conservation of mass and ${\displaystyle y}$-momentum requires ${\displaystyle v=0,\ p=p_{\infty }}$ everywhere in the flow domain. Conservation of energy and ${\displaystyle x}$-momentum reduce to

${\displaystyle {\frac {d}{dy}}\left(\mu {\frac {du}{dy}}\right)=0,\quad \Rightarrow \quad {\frac {d\tau }{dy}}=0,\quad \Rightarrow \quad \tau =\tau _{w}}$

${\displaystyle {\frac {1}{\mathrm {Pr} }}{\frac {d}{dy}}\left(\mu {\frac {dh}{dy}}\right)+\mu \left({\frac {du}{dy}}\right)^{2}=0.}$

where ${\displaystyle \tau =\tau _{w}={\text{constant}}}$ is the wall shear stress. The flow does not depend on the Reynolds number ${\displaystyle \mathrm {Re} =Ul/\nu _{\infty }}$, but rather on the Prandtl number ${\displaystyle \mathrm {Pr} =\mu _{\infty }c_{p\infty }/\kappa _{\infty }}$ and the Mach number ${\displaystyle \mathrm {M} =U/c_{\infty }=U/{\sqrt {(\gamma -1)h_{\infty }}}}$, where ${\displaystyle \kappa }$ is the thermal conductivity, ${\displaystyle c}$ is the speed of sound and ${\displaystyle \gamma }$ is the specific heat ratio. Introduce the non-dimensional variables

${\displaystyle {\tilde {y}}={\frac {y}{l}},\quad {\tilde {T}}={\frac {T}{T_{\infty }}},\quad {\tilde {T}}_{w}={\frac {T_{w}}{T_{\infty }}},\quad {\tilde {h}}={\frac {h}{h_{\infty }}},\quad {\tilde {h}}_{w}={\frac {h_{w}}{h_{\infty }}},\quad {\tilde {u}}={\frac {u}{U}},\quad {\tilde {\mu }}={\frac {\mu }{\mu _{\infty }}},\quad {\tilde {\tau }}_{w}={\frac {\tau _{w}}{\mu _{\infty }U/l}}}$

In terms of these quantities, the solutions are

${\displaystyle {\tilde {h}}={\tilde {h}}_{w}+\left[{\frac {\gamma -1}{2}}\mathrm {M} ^{2}\mathrm {Pr} +(1-{\tilde {h}}_{w})\right]{\tilde {u}}-{\frac {\gamma -1}{2}}\mathrm {M} ^{2}\mathrm {Pr} \,{\tilde {u}}^{2},}$

${\displaystyle {\tilde {y}}={\frac {1}{{\tilde {\tau }}_{w}}}\int _{0}^{\tilde {u}}{\tilde {\mu }}\,d{\tilde {u}},\quad {\tilde {\tau }}_{w}=\int _{0}^{1}{\tilde {\mu }}\,d{\tilde {u}},\quad q_{w}=-{\frac {1}{\mathrm {Pr} }}\tau _{w}\left({\frac {dh}{du}}\right)_{w},}$

where ${\displaystyle q_{w}}$ is the heat transferred per unit time per unit area from the lower wall. Thus ${\displaystyle {\tilde {h}},{\tilde {T}},{\tilde {u}},{\tilde {\mu }}}$ are implicit functions of ${\displaystyle y}$. One can also write the solution in terms of the recovery temperature ${\displaystyle T_{r}}$ and recovery enthalpy ${\displaystyle h_{r}}$ evaluated at the temperature of an insulated wall i.e., the values of ${\displaystyle T_{w}}$ and ${\displaystyle h_{w}}$ for which ${\displaystyle q_{w}=0}$.^{[ clarification needed ]} Then the solution is

${\displaystyle {\frac {q_{w}}{\tau _{w}U}}={\frac {{\tilde {T}}_{w}-{\tilde {T}}_{r}}{(\gamma -1)\mathrm {M} ^{2}\mathrm {Pr} }},\quad {\tilde {T}}_{r}=1+{\frac {\gamma -1}{2}}\mathrm {M} ^{2}\mathrm {Pr} ,}$

${\displaystyle {\tilde {h}}={\tilde {h}}_{w}+({\tilde {h}}_{r}-{\tilde {h}}_{w}){\tilde {u}}-{\frac {\gamma -1}{2}}\mathrm {M} ^{2}\mathrm {Pr} \,{\tilde {u}}^{2}.}$

If the specific heat is constant, then ${\displaystyle {\tilde {h}}={\tilde {T}}}$. When ${\displaystyle \mathrm {M} \rightarrow 0}$ and ${\displaystyle T_{w}=T_{\infty },\Rightarrow q_{w}=0}$, then ${\displaystyle T}$ and ${\displaystyle \mu }$ are constant everywhere, thus recovering the incompressible Couette flow solution. Otherwise, one must know the full temperature dependence of ${\displaystyle {\tilde {\mu }}({\tilde {T}})}$. While there is no simple expression for ${\displaystyle {\tilde {\mu }}({\tilde {T}})}$ that is both accurate and general, there are several approximations for certain materials — see, e.g., temperature dependence of viscosity. When ${\displaystyle \mathrm {M} \rightarrow 0}$ and ${\displaystyle q_{w}\neq 0}$, the recovery quantities become unity ${\displaystyle {\tilde {T}}_{r}=1}$. For air, the values ${\displaystyle \gamma =1.4,\ {\tilde {\mu }}({\tilde {T}})={\tilde {T}}^{2/3}}$ are commonly used, and the results for this case are shown in the figure.

The effects of dissociation and ionization (i.e., ${\displaystyle c_{p}}$ is not constant) have also been studied; in that case the recovery temperature is reduced by the dissociation of molecules. ^[7]

Rectangular channel

Couette flow for square channel

Couette flow with h/l=0.1

One-dimensional flow ${\displaystyle u(y)}$ is valid when both plates are infinitely long in the streamwise (${\displaystyle x}$) and spanwise (${\displaystyle z}$) directions. When the spanwise length is finite, the flow becomes two-dimensional and ${\displaystyle u}$ is a function of both ${\displaystyle y}$ and ${\displaystyle z}$. However, the infinite length in the streamwise direction must be retained in order to ensure the unidirectional nature of the flow.

As an example, consider an infinitely long rectangular channel with transverse height ${\displaystyle h}$ and spanwise width ${\displaystyle l}$, subject to the condition that the top wall moves with a constant velocity ${\displaystyle U}$. Without an imposed pressure gradient, the Navier–Stokes equations reduce to

${\displaystyle {\frac {\partial ^{2}u}{\partial y^{2}}}+{\frac {\partial ^{2}u}{\partial z^{2}}}=0}$

with boundary conditions

${\displaystyle u(0,z)=0,\quad u(h,z)=U,}$

${\displaystyle u(y,0)=0,\quad u(y,l)=0.}$

Using separation of variables, the solution is given by

${\displaystyle u(y,z)={\frac {4U}{\pi }}\sum _{n=1}^{\infty }{\frac {1}{2n-1}}{\frac {\sinh(\beta _{n}y)}{\sinh(\beta _{n}h)}}\sin(\beta _{n}z),\quad \beta _{n}={\frac {(2n-1)\pi }{l}}.}$

When ${\displaystyle h/l\ll 1}$, the planar Couette flow is recovered, as shown in the figure.

Coaxial cylinders

Taylor–Couette flow is a flow between two rotating, infinitely long, coaxial cylinders. ^[8] The original problem was solved by Stokes in 1845, ^[9] but Geoffrey Ingram Taylor's name was attached to the flow because he studied its stability in a famous 1923 paper. ^[10]

The problem can be solved in cylindrical coordinates ${\displaystyle (r,\theta ,z)}$. Denote the radii of the inner and outer cylinders as ${\displaystyle R_{1}}$ and ${\displaystyle R_{2}}$. Assuming the cylinders rotate at constant angular velocities ${\displaystyle \Omega _{1}}$ and ${\displaystyle \Omega _{2}}$, then the velocity in the ${\displaystyle \theta }$-direction is ^[11]

${\displaystyle v_{\theta }(r)=ar+{\frac {b}{r}},\qquad a={\frac {\Omega _{2}R_{2}^{2}-\Omega _{1}R_{1}^{2}}{R_{2}^{2}-R_{1}^{2}}},\quad b={\frac {(\Omega _{1}-\Omega _{2})R_{1}^{2}R_{2}^{2}}{R_{2}^{2}-R_{1}^{2}}}.}$

This equation shows that the effects of curvature no longer allow for constant shear in the flow domain.

Coaxial cylinders of finite length

The classical Taylor–Couette flow problem assumes infinitely long cylinders; if the cylinders have non-negligible finite length ${\displaystyle l}$, then the analysis must be modified (though the flow is still unidirectional). For ${\displaystyle \Omega _{2}=0}$, the finite-length problem can be solved using separation of variables or integral transforms, giving: ^[12]

${\displaystyle v_{\theta }(r,z)={\frac {4R_{1}\Omega _{1}}{\pi }}\sum _{n=1}^{\infty }{\frac {1}{2n-1}}{\frac {I_{1}(\beta _{n}R_{2})K_{1}(\beta _{n}r)-K_{1}(\beta _{n}R_{2})I_{1}(\beta _{n}r)}{I_{1}(\beta _{n}R_{2})K_{1}(\beta _{n}R_{1})-K_{1}(\beta _{n}R_{2})I_{1}(\beta _{n}R_{1})}}\sin(\beta _{n}z),\quad \beta _{n}={\frac {(2n-1)\pi }{l}},}$

where ${\displaystyle I(\beta _{n}r),\ K(\beta _{n}r)}$ are the Modified Bessel functions of the first and second kind.

See also

• Laminar flow
• Stokes-Couette flow
• Hagen–Poiseuille equation
• Taylor–Couette flow
• Hagen–Poiseuille flow from the Navier–Stokes equations

References

1. Zhilenko et al. (2018)
2. Guyon et al. (2001), p. 136
3. Heller (1960)
4. Pozrikidis (2011), pp. 338–339
5. Kundu et al. (2016), p. 415
6. Lagerstrom (1996)
7. Liepmann et al. (1956, 1957)
8. Landau and Lifshitz (1987)
9. Stokes (1845)
10. Taylor (1923)
11. Guyon et al. (2001), pp. 163–166
12. Wendl (1999)

Sources

• Acheson, D.J. (1990). Elementary Fluid Dynamics. Oxford University Press. ISBN   0-19-859679-0.
• Batchelor, G.K. (2000) [1967]. An Introduction to Fluid Dynamics. Cambridge University Press. ISBN   0-521-66396-2.
• Guyon, Etienne; Hulin, Jean-Pierre; Petit, Luc; Mitescu, Catalin D. (2001). Physical Hydrodynamics. Oxford University Press. ISBN   0-19-851746-7.
• Heller, John P. (1960). "An Unmixing Demonstration". American Journal of Physics. 28 (4): 348–353. Bibcode:1960AmJPh..28..348H. doi:10.1119/1.1935802. ISSN   0002-9505.
• Illingworth, C. R. (1950). "Some solutions of the equations of flow of a viscous compressible fluid". Mathematical Proceedings of the Cambridge Philosophical Society. 46 (3): 469–478. Bibcode:1950PCPS...46..469I. doi:10.1017/S0305004100025986. ISSN   0305-0041. S2CID   122559614.
• Kundu, Pijush K.; Cohen, Ira M.; Dowling, David R. (2016). Fluid Mechanics (6th ed.). Elsevier. ISBN   978-0-12-405935-1.
• Lagerstrom, Paco (1996). Laminar flow theory. Princeton University Press. ISBN   978-0691025988.
• Landau, L. D.; Lifshitz, E.M. (1987). Fluid Mechanics (2nd ed.). Elsevier. ISBN   978-0-08-057073-0.
• Liepmann, H. W., and Z. O. Bleviss. "The effects of dissociation and ionization on compressible couette flow." Douglas Aircraft Co. Rept. SM-19831 130 (1956).
• Liepmann, Hans Wolfgang, and Anatol Roshko. Elements of gasdynamics. Courier Corporation, 1957.
• Pozrikidis, C. (2011). Introduction to Theoretical and Computational Fluid Dynamics. Oxford University Press. ISBN   978-0-19-975207-2.
• Richard Feynman (1964) The Feynman Lectures on Physics: Mainly Electromagnetism and Matter, § 41–6 Couette flow, Addison–Wesley ISBN   0-201-02117-X
• Stokes, George Gabriel (1880). "On the Theories of the Internal Friction of Fluids in Motion, and of the Equilibrium and Motion of Elastic Solids". Mathematical and Physical Papers. Cambridge University Press: 75–129. doi:10.1017/CBO9780511702242.005. ISBN   9780511702242.
• Taylor, Geoffrey I. (1923). "Stability of a viscous liquid contained between two rotating cylinders". Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character. 223 (605–615): 289–343. Bibcode:1923RSPTA.223..289T. doi: 10.1098/rsta.1923.0008 . JSTOR   91148.
• Wendl, Michael C. (1999). "General solution for the Couette flow profile". Physical Review E. 60 (5): 6192–6194. Bibcode:1999PhRvE..60.6192W. doi:10.1103/PhysRevE.60.6192. ISSN   1063-651X. PMID   11970531.
• Zhilenko, Dmitry; Krivonosova, Olga; Gritsevich, Maria; Read, Peter (2018). "Wave number selection in the presence of noise: Experimental results". Chaos: An Interdisciplinary Journal of Nonlinear Science. 28 (5): 053110. Bibcode:2018Chaos..28e3110Z. doi:10.1063/1.5011349. hdl: 10138/240787 . ISSN   1054-1500. PMID   29857673. S2CID   46925417.

External links

• AMS Glossary: Couette Flow
• A rheologists perspective: the science behind the couette cell accessory