
In mathematics, a diffeomorphism is an isomorphism of smooth manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are differentiable.

In mathematics, an elliptic curve is a smooth, projective, algebraic curve of genus one, on which there is a specified point O. An elliptic curve is defined over a field K and describes points in K2, the Cartesian product of K with itself. If the field's characteristic is different from 2 and 3, then the curve can be described as a plane algebraic curve which consists of solutions (x, y) for:
In differential geometry, a subject of mathematics, a symplectic manifold is a smooth manifold, , equipped with a closed nondegenerate differential 2-form , called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology. Symplectic manifolds arise naturally in abstract formulations of classical mechanics and analytical mechanics as the cotangent bundles of manifolds. For example, in the Hamiltonian formulation of classical mechanics, which provides one of the major motivations for the field, the set of all possible configurations of a system is modeled as a manifold, and this manifold's cotangent bundle describes the phase space of the system.

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is said to be a tangent of a curve y = f(x) at a point x = c if the line passes through the point (c, f ) on the curve and has slope f'(c), where f' is the derivative of f. A similar definition applies to space curves and curves in n-dimensional Euclidean space.
In mathematics, a singularity is a point at which a given mathematical object is not defined, or a point where the mathematical object ceases to be well-behaved in some particular way, such as by lacking differentiability or analyticity.
In mathematics, the discriminant of a polynomial is a quantity that depends on the coefficients and allows deducing some properties of the roots without computing them. More precisely, it is a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factoring, number theory, and algebraic geometry.

In differential geometry, the tangent bundle of a differentiable manifold is a manifold which assembles all the tangent vectors in . As a set, it is given by the disjoint union of the tangent spaces of . That is,

In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation h(x, y, t) = 0 can be restricted to the affine algebraic plane curve of equation h(x, y, 1) = 0. These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered.
In mathematics, specifically in differential topology, Morse theory enables one to analyze the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a typical differentiable function on a manifold will reflect the topology quite directly. Morse theory allows one to find CW structures and handle decompositions on manifolds and to obtain substantial information about their homology.
This is a glossary of some terms used in Riemannian geometry and metric geometry — it doesn't cover the terminology of differential topology.
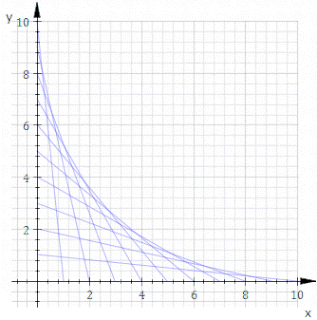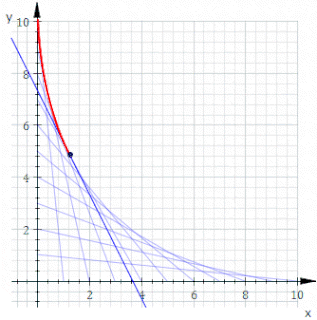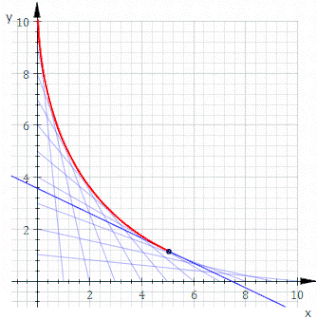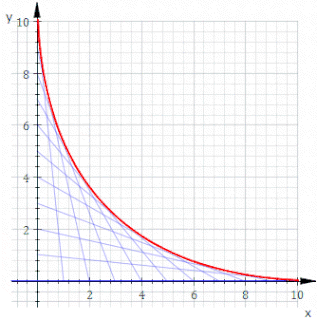
In geometry, an envelope of a planar family of curves is a curve that is tangent to each member of the family at some point, and these points of tangency together form the whole envelope. Classically, a point on the envelope can be thought of as the intersection of two "infinitesimally adjacent" curves, meaning the limit of intersections of nearby curves. This idea can be generalized to an envelope of surfaces in space, and so on to higher dimensions.
In mathematics, the Teichmüller space of a (real) topological surface , is a space that parametrizes complex structures on up to the action of homeomorphisms that are isotopic to the identity homeomorphism. Teichmüller spaces are named after Oswald Teichmüller.
In mathematical analysis, more precisely in microlocal analysis, the wave front (set) WF(f) characterizes the singularities of a generalized function f, not only in space, but also with respect to its Fourier transform at each point. The term "wave front" was coined by Lars Hörmander around 1970.

Critical point is a wide term used in many branches of mathematics.

In mathematics, a crunode (archaic) or node is a point where a curve intersects itself so that both branches of the curve have distinct tangent lines at the point of intersection. A crunode is also known as an ordinary double point.

In projective geometry, a dual curve of a given plane curve C is a curve in the dual projective plane consisting of the set of lines tangent to C. There is a map from a curve to its dual, sending each point to the point dual to its tangent line. If C is algebraic then so is its dual and the degree of the dual is known as the class of the original curve. The equation of the dual of C, given in line coordinates, is known as the tangential equation of C. Duality is an involution: the dual of the dual of C is the original curve C.
In geometry, a singular point on a curve is one where the curve is not given by a smooth embedding of a parameter. The precise definition of a singular point depends on the type of curve being studied.
In classical algebraic geometry, a tacnode is a kind of singular point of a curve. It is defined as a point where two osculating circles to the curve at that point are tangent. This means that two branches of the curve have ordinary tangency at the double point.
In mathematics, and particularly singularity theory, the Milnor number, named after John Milnor, is an invariant of a function germ.
In mathematics, and especially affine differential geometry, the affine focal set of a smooth submanifold M embedded in a smooth manifold N is the caustic generated by the affine normal lines. It can be realised as the bifurcation set of a certain family of functions. The bifurcation set is the set of parameter values of the family which yield functions with degenerate singularities. This is not the same as the bifurcation diagram in dynamical systems.



































