
In mathematics, a time series is a series of data points indexed in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. Examples of time series are heights of ocean tides, counts of sunspots, and the daily closing value of the Dow Jones Industrial Average.
In the statistical analysis of time series, autoregressive–moving-average (ARMA) models provide a parsimonious description of a (weakly) stationary stochastic process in terms of two polynomials, one for the autoregression (AR) and the second for the moving average (MA). The general ARMA model was described in the 1951 thesis of Peter Whittle, Hypothesis testing in time series analysis, and it was popularized in the 1970 book by George E. P. Box and Gwilym Jenkins.
Functional data analysis (FDA) is a branch of statistics that analyses data providing information about curves, surfaces or anything else varying over a continuum. In its most general form, under an FDA framework, each sample element of functional data is considered to be a random function. The physical continuum over which these functions are defined is often time, but may also be spatial location, wavelength, probability, etc. Intrinsically, functional data are infinite dimensional. The high intrinsic dimensionality of these data brings challenges for theory as well as computation, where these challenges vary with how the functional data were sampled. However, the high or infinite dimensional structure of the data is a rich source of information and there are many interesting challenges for research and data analysis.
A portmanteau test is a type of statistical hypothesis test in which the null hypothesis is well specified, but the alternative hypothesis is more loosely specified. Tests constructed in this context can have the property of being at least moderately powerful against a wide range of departures from the null hypothesis. Thus, in applied statistics, a portmanteau test provides a reasonable way of proceeding as a general check of a model's match to a dataset where there are many different ways in which the model may depart from the underlying data generating process. Use of such tests avoids having to be very specific about the particular type of departure being tested.
In statistics, the Lilliefors test is a normality test based on the Kolmogorov–Smirnov test. It is used to test the null hypothesis that data come from a normally distributed population, when the null hypothesis does not specify which normal distribution; i.e., it does not specify the expected value and variance of the distribution. It is named after Hubert Lilliefors, professor of statistics at George Washington University.
Chi-square automatic interaction detection (CHAID) is a decision tree technique based on adjusted significance testing. The technique was developed in South Africa and was published in 1980 by Gordon V. Kass, who had completed a PhD thesis on this topic. CHAID can be used for prediction as well as classification, and for detection of interaction between variables. CHAID is based on a formal extension of AID and THAID procedures of the 1960s and 1970s, which in turn were extensions of earlier research, including that performed by Belson in the UK in the 1950s. A history of earlier supervised tree methods together with a detailed description of the original CHAID algorithm and the exhaustive CHAID extension by Biggs, De Ville, and Suen, can be found in Ritschard.

Computational statistics, or statistical computing, is the bond between statistics and computer science. It means statistical methods that are enabled by using computational methods. It is the area of computational science specific to the mathematical science of statistics. This area is also developing rapidly, leading to calls that a broader concept of computing should be taught as part of general statistical education.
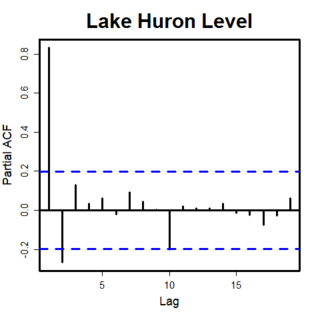
In time series analysis, the partial autocorrelation function (PACF) gives the partial correlation of a stationary time series with its own lagged values, regressed the values of the time series at all shorter lags. It contrasts with the autocorrelation function, which does not control for other lags.

Howell Tong is a statistician who has made fundamental contributions to nonlinear time series analysis, semi-parametric statistics, non-parametric statistics, dimension reduction, model selection, likelihood-free statistics and other areas. In the words of Professor Peter Whittle (FRS): "The striking feature of Howell Tong's … is the continuing freshness, boldness and spirit of enquiry which inform them-indeed, proper qualities for an explorer. He stands as the recognised innovator and authority in his subject, while remaining disarmingly direct and enthusiastic." His work, in the words of Sir David Cox, "links two fascinating fields, nonlinear time series and deterministic dynamical systems." He is the father of the threshold time series models, which have extensive applications in ecology, economics, epidemiology and finance. Besides nonlinear time series analysis, he was the co-author of a seminal paper, which he read to the Royal Statistical Society, on dimension reduction in semi-parametric statistics by pioneering the approach based on minimum average variance estimation. He has also made numerous novel contributions to nonparametric statistics, Markov chain modelling, reliability, non-stationary time series analysis and wavelets.
Matching is a statistical technique which is used to evaluate the effect of a treatment by comparing the treated and the non-treated units in an observational study or quasi-experiment. The goal of matching is to reduce bias for the estimated treatment effect in an observational-data study, by finding, for every treated unit, one non-treated unit(s) with similar observable characteristics against which the covariates are balanced out. By matching treated units to similar non-treated units, matching enables a comparison of outcomes among treated and non-treated units to estimate the effect of the treatment reducing bias due to confounding. Propensity score matching, an early matching technique, was developed as part of the Rubin causal model, but has been shown to increase model dependence, bias, inefficiency, and power and is no longer recommended compared to other matching methods. A simple, easy-to-understand, and statistically powerful method of matching known as Coarsened Exact Matching or CEM.
John Winsor Pratt is Emeritus William Ziegler professor business administration at Harvard University. His former education was conducted at Princeton and Stanford, where he specialized in mathematics and statistics. Pratt spent most of his academic career at Harvard University. He was an editor of the Journal of the American Statistical Association from 1965 to 1970. His researches on risk aversion, risk sharing incentives, and the nature and discovery of stochastic laws, statistical relationships that describe the effects of decisions. He has made contributions to research in risk aversion theory, notably with Kenneth Arrow on measures of risk aversion.
Sudipto Banerjee is an Indian-American statistician best known for his work on Bayesian hierarchical modeling and inference for spatial data analysis. He is Professor and Chair of the Department of Biostatistics in the School of Public Health at the University of California, Los Angeles. He served as the 2022 President of the International Society for Bayesian Analysis.
Paul R. Rosenbaum is the Robert G. Putzel Professor Emeritus in the Department of Statistics and Data Science at Wharton School of the University of Pennsylvania, where he worked from 1986 through 2021. He has written extensively about causal inference in observational studies, including sensitivity analysis, optimal matching, design sensitivity, evidence factors, quasi-experimental devices, and the propensity score. With various coauthors, he has also written about health outcomes, racial disparities in health outcomes, instrumental variables, psychometrics and experimental design.
Alan Enoch Gelfand is an American statistician, and is currently the James B. Duke Professor of Statistics and Decision Sciences at Duke University. Gelfand’s research includes substantial contributions to the fields of Bayesian statistics, spatial statistics and hierarchical modeling.
Colin Lingwood Mallows is an English statistician, who has worked in the United States since 1960. He is known for Mallows's Cp, a regression model diagnostic procedure, widely used in regression analysis and the Fowlkes–Mallows index, a popular clustering validation criterion.

Éric Moulines is a French researcher in statistical learning and signal processing. He received the silver medal from the CNRS in 2010, the France Télécom prize awarded in collaboration with the French Academy of Sciences in 2011. He was appointed a Fellow of the European Association for Signal Processing in 2012 and of the Institute of Mathematical Statistics in 2016. He is General Engineer of the Corps des Mines (X81).
Babette Anne Brumback is an American biostatistician known for her work on causal inference. She is a professor of biostatistics at the University of Florida.
Recurrent event analysis is a branch of survival analysis that analyzes the time until recurrences occur, such as recurrences of traits or diseases. Recurrent events are often analysed in social sciences and medical studies, for example recurring infections, depressions or cancer recurrences. Recurrent event analysis attempts to answer certain questions, such as: how many recurrences occur on average within a certain time interval? Which factors are associated with a higher or lower risk of recurrence?
Michael David Escobar is an American biostatistician who is known for Bayesian nonparametrics, mixture models.
John Anthony Hartigan is an Australian-American statistician, the Eugene Higgins Professor of Statistics emeritus at Yale University. He made fundamental contributions to clustering algorithms, including the famous Hartigan-Wong method and biclustering, and Bayesian statistics.





