In statistics, a location parameter of a probability distribution is a scalar- or vector-valued parameter , which determines the "location" or shift of the distribution. In the literature of location parameter estimation, the probability distributions with such parameter are found to be formally defined in one of the following equivalent ways:
In statistics, the likelihood-ratio test assesses the goodness of fit of two competing statistical models, specifically one found by maximization over the entire parameter space and another found after imposing some constraint, based on the ratio of their likelihoods. If the constraint is supported by the observed data, the two likelihoods should not differ by more than sampling error. Thus the likelihood-ratio test tests whether this ratio is significantly different from one, or equivalently whether its natural logarithm is significantly different from zero.
In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of an assumed probability distribution, given some observed data. This is achieved by maximizing a likelihood function so that, under the assumed statistical model, the observed data is most probable. The point in the parameter space that maximizes the likelihood function is called the maximum likelihood estimate. The logic of maximum likelihood is both intuitive and flexible, and as such the method has become a dominant means of statistical inference.
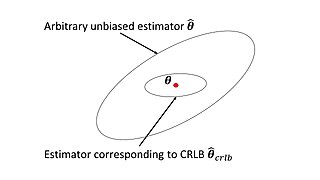
In estimation theory and statistics, the Cramér–Rao bound (CRB) relates to estimation of a deterministic parameter. The result is named in honor of Harald Cramér and C. R. Rao, but has also been derived independently by Maurice Fréchet, Georges Darmois, and by Alexander Aitken and Harold Silverstone. It is also known as Fréchet-Cramér–Rao or Fréchet-Darmois-Cramér-Rao lower bound. It states that the precision of any unbiased estimator is at most the Fisher information; or (equivalently) the reciprocal of the Fisher information is a lower bound on its variance.
In mathematical statistics, the Fisher information is a way of measuring the amount of information that an observable random variable X carries about an unknown parameter θ of a distribution that models X. Formally, it is the variance of the score, or the expected value of the observed information.
In mathematics, the Riesz–Thorin theorem, often referred to as the Riesz–Thorin interpolation theorem or the Riesz–Thorin convexity theorem, is a result about interpolation of operators. It is named after Marcel Riesz and his student G. Olof Thorin.

In statistics, a consistent estimator or asymptotically consistent estimator is an estimator—a rule for computing estimates of a parameter θ0—having the property that as the number of data points used increases indefinitely, the resulting sequence of estimates converges in probability to θ0. This means that the distributions of the estimates become more and more concentrated near the true value of the parameter being estimated, so that the probability of the estimator being arbitrarily close to θ0 converges to one.
In statistics a minimum-variance unbiased estimator (MVUE) or uniformly minimum-variance unbiased estimator (UMVUE) is an unbiased estimator that has lower variance than any other unbiased estimator for all possible values of the parameter.
In Bayesian probability, the Jeffreys prior, named after Sir Harold Jeffreys, is a non-informative prior distribution for a parameter space; its density function is proportional to the square root of the determinant of the Fisher information matrix:
In statistics, a parametric model or parametric family or finite-dimensional model is a particular class of statistical models. Specifically, a parametric model is a family of probability distributions that has a finite number of parameters.
In estimation theory and decision theory, a Bayes estimator or a Bayes action is an estimator or decision rule that minimizes the posterior expected value of a loss function. Equivalently, it maximizes the posterior expectation of a utility function. An alternative way of formulating an estimator within Bayesian statistics is maximum a posteriori estimation.
In statistics, Basu's theorem states that any boundedly complete minimal sufficient statistic is independent of any ancillary statistic. This is a 1955 result of Debabrata Basu.
In statistical decision theory, where we are faced with the problem of estimating a deterministic parameter (vector) from observations an estimator is called minimax if its maximal risk is minimal among all estimators of . In a sense this means that is an estimator which performs best in the worst possible case allowed in the problem.
In statistics, identifiability is a property which a model must satisfy for precise inference to be possible. A model is identifiable if it is theoretically possible to learn the true values of this model's underlying parameters after obtaining an infinite number of observations from it. Mathematically, this is equivalent to saying that different values of the parameters must generate different probability distributions of the observable variables. Usually the model is identifiable only under certain technical restrictions, in which case the set of these requirements is called the identification conditions.
In statistics, the Hájek–Le Cam convolution theorem states that any regular estimator in a parametric model is asymptotically equivalent to a sum of two independent random variables, one of which is normal with asymptotic variance equal to the inverse of Fisher information, and the other having arbitrary distribution.
In statistics, asymptotic theory, or large sample theory, is a framework for assessing properties of estimators and statistical tests. Within this framework, it is often assumed that the sample size n may grow indefinitely; the properties of estimators and tests are then evaluated under the limit of n → ∞. In practice, a limit evaluation is considered to be approximately valid for large finite sample sizes too.
In statistics, efficiency is a measure of quality of an estimator, of an experimental design, or of a hypothesis testing procedure. Essentially, a more efficient estimator needs fewer input data or observations than a less efficient one to achieve the Cramér–Rao bound. An efficient estimator is characterized by having the smallest possible variance, indicating that there is a small deviance between the estimated value and the "true" value in the L2 norm sense.
In statistics, local asymptotic normality is a property of a sequence of statistical models, which allows this sequence to be asymptotically approximated by a normal location model, after an appropriate rescaling of the parameter. An important example when the local asymptotic normality holds is in the case of i.i.d sampling from a regular parametric model.
In Bayesian inference, the Bernstein–von Mises theorem provides the basis for using Bayesian credible sets for confidence statements in parametric models. It states that under some conditions, a posterior distribution converges in the limit of infinite data to a multivariate normal distribution centered at the maximum likelihood estimator with covariance matrix given by , where is the true population parameter and is the Fisher information matrix at the true population parameter value:
In mathematics, the Poisson boundary is a measure space associated to a random walk. It is an object designed to encode the asymptotic behaviour of the random walk, i.e. how trajectories diverge when the number of steps goes to infinity. Despite being called a boundary it is in general a purely measure-theoretical object and not a boundary in the topological sense. However, in the case where the random walk is on a topological space the Poisson boundary can be related to the Martin boundary, which is an analytic construction yielding a genuine topological boundary. Both boundaries are related to harmonic functions on the space via generalisations of the Poisson formula.























































