
The group velocity of a wave is the velocity with which the overall envelope shape of the wave's amplitudes—known as the modulation or envelope of the wave—propagates through space.

The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity. The phase velocity is given in terms of the wavelength λ (lambda) and time period T as

In physics and mathematics, wavelength or spatial period of a wave or periodic function is the distance over which the wave's shape repeats. In other words, it is the distance between consecutive corresponding points of the same phase on the wave, such as two adjacent crests, troughs, or zero crossings. Wavelength is a characteristic of both traveling waves and standing waves, as well as other spatial wave patterns. The inverse of the wavelength is called the spatial frequency. Wavelength is commonly designated by the Greek letter lambda (λ). The term "wavelength" is also sometimes applied to modulated waves, and to the sinusoidal envelopes of modulated waves or waves formed by interference of several sinusoids.
The propagation constant of a sinusoidal electromagnetic wave is a measure of the change undergone by the amplitude and phase of the wave as it propagates in a given direction. The quantity being measured can be the voltage, the current in a circuit, or a field vector such as electric field strength or flux density. The propagation constant itself measures the change per unit length, but it is otherwise dimensionless. In the context of two-port networks and their cascades, propagation constant measures the change undergone by the source quantity as it propagates from one port to the next.
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, specifically in solids and some liquids. A type of quasiparticle, a phonon is an excited state in the quantum mechanical quantization of the modes of vibrations for elastic structures of interacting particles. Phonons can be thought of as quantized sound waves, similar to photons as quantized light waves. However, photons are fundamental particles that can be individually detected, whereas phonons, being quasiparticles, are an emergent phenomenon.
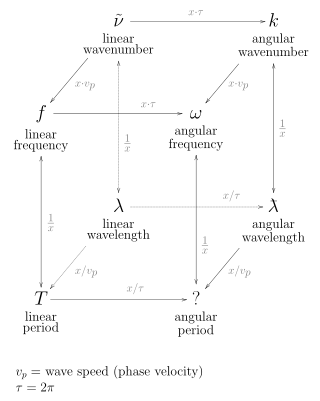
In the physical sciences, the wavenumber, also known as repetency, is the spatial frequency of a wave, measured in cycles per unit distance or radians per unit distance. It is analogous to temporal frequency, which is defined as the number of wave cycles per unit time or radians per unit time.
A wavenumber–frequency diagram is a plot displaying the relationship between the wavenumber and the frequency of certain phenomena. Usually frequencies are placed on the vertical axis, while wavenumbers are placed on the horizontal axis.

In optics and in wave propagation in general, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency; sometimes the term chromatic dispersion is used for specificity to optics in particular. A medium having this common property may be termed a dispersive medium.
Matter waves are a central part of the theory of quantum mechanics, being half of wave–particle duality. All matter exhibits wave-like behavior. For example, a beam of electrons can be diffracted just like a beam of light or a water wave.

In thermodynamics and solid-state physics, the Debye model is a method developed by Peter Debye in 1912 for estimating the phonon contribution to the specific heat in a solid. It treats the vibrations of the atomic lattice (heat) as phonons in a box, in contrast to the Einstein photoelectron model, which treats the solid as many individual, non-interacting quantum harmonic oscillators. The Debye model correctly predicts the low-temperature dependence of the heat capacity of solids, which is proportional to – the Debye T 3 law. Similarly to the Einstein photoelectron model, it recovers the Dulong–Petit law at high temperatures. Due to simplifying assumptions, its accuracy suffers at intermediate temperatures.

A capillary wave is a wave traveling along the phase boundary of a fluid, whose dynamics and phase velocity are dominated by the effects of surface tension.
In physics, a wave vector is a vector used in describing a wave, with a typical unit being cycle per metre. It has a magnitude and direction. Its magnitude is the wavenumber of the wave, and its direction is perpendicular to the wavefront. In isotropic media, this is also the direction of wave propagation.
The Compton wavelength is a quantum mechanical property of a particle, defined as the wavelength of a photon whose energy is the same as the rest energy of that particle. It was introduced by Arthur Compton in 1923 in his explanation of the scattering of photons by electrons.
In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, with gravity and surface tension as the restoring forces. As a result, water with a free surface is generally considered to be a dispersive medium.
The theoretical and experimental justification for the Schrödinger equation motivates the discovery of the Schrödinger equation, the equation that describes the dynamics of nonrelativistic particles. The motivation uses photons, which are relativistic particles with dynamics described by Maxwell's equations, as an analogue for all types of particles.

In fluid dynamics, wave shoaling is the effect by which surface waves, entering shallower water, change in wave height. It is caused by the fact that the group velocity, which is also the wave-energy transport velocity, changes with water depth. Under stationary conditions, a decrease in transport speed must be compensated by an increase in energy density in order to maintain a constant energy flux. Shoaling waves will also exhibit a reduction in wavelength while the frequency remains constant.
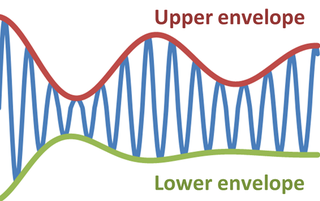
In physics and engineering, the envelope of an oscillating signal is a smooth curve outlining its extremes. The envelope thus generalizes the concept of a constant amplitude into an instantaneous amplitude. The figure illustrates a modulated sine wave varying between an upper envelope and a lower envelope. The envelope function may be a function of time, space, angle, or indeed of any variable.
Hopfield dielectric – in quantum mechanics a model of dielectric consisting of quantum harmonic oscillators interacting with the modes of the quantum electromagnetic field. The collective interaction of the charge polarization modes with the vacuum excitations, photons leads to the perturbation of both the linear dispersion relation of photons and constant dispersion of charge waves by the avoided crossing between the two dispersion lines of polaritons. Similarly to the acoustic and the optical phonons and far from the resonance one branch is photon-like while the other charge wave-like. Mathematically the Hopfield dielectric for the one mode of excitation is equivalent to the Trojan wave packet in the harmonic approximation. The Hopfield model of the dielectric predicts the existence of eternal trapped frozen photons similar to the Hawking radiation inside the matter with the density proportional to the strength of the matter-field coupling.
Brillouin spectroscopy is an empirical spectroscopy technique which allows the determination of elastic moduli of materials. The technique uses inelastic scattering of light when it encounters acoustic phonons in a crystal, a process known as Brillouin scattering, to determine phonon energies and therefore interatomic potentials of a material. The scattering occurs when an electromagnetic wave interacts with a density wave, photon-phonon scattering.
The Planck relation is a fundamental equation in quantum mechanics which states that the energy of a photon, E, known as photon energy, is proportional to its frequency, ν:








































