In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.

In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity , a number ranging from to .

In mathematics, a linear equation is an equation that may be put in the form where are the variables, and are the coefficients, which are often real numbers. The coefficients may be considered as parameters of the equation and may be arbitrary expressions, provided they do not contain any of the variables. To yield a meaningful equation, the coefficients are required to not all be zero.

In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.
In Euclidean geometry, a plane is a flat two-dimensional surface that extends indefinitely. Euclidean planes often arise as subspaces of three-dimensional space . A prototypical example is one of a room's walls, infinitely extended and assumed infinitesimal thin. While a pair of real numbers suffices to describe points on a plane, the relationship with out-of-plane points requires special consideration for their embedding in the ambient space .

An ellipsoid is a surface that can be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.

In geometry, a normal is an object that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the line perpendicular to the tangent line to the curve at the point.
In mathematics, the matrix representation of conic sections permits the tools of linear algebra to be used in the study of conic sections. It provides easy ways to calculate a conic section's axis, vertices, tangents and the pole and polar relationship between points and lines of the plane determined by the conic. The technique does not require putting the equation of a conic section into a standard form, thus making it easier to investigate those conic sections whose axes are not parallel to the coordinate system.
The Huzita–Justin axioms or Huzita–Hatori axioms are a set of rules related to the mathematical principles of origami, describing the operations that can be made when folding a piece of paper. The axioms assume that the operations are completed on a plane, and that all folds are linear. These are not a minimal set of axioms but rather the complete set of possible single folds.
In vector calculus, Green's theorem relates a line integral around a simple closed curve C to a double integral over the plane region D bounded by C. It is the two-dimensional special case of Stokes' theorem.
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the base form

In mathematics, a pedal curve of a given curve results from the orthogonal projection of a fixed point on the tangent lines of this curve. More precisely, for a plane curve C and a given fixed pedal pointP, the pedal curve of C is the locus of points X so that the line PX is perpendicular to a tangent T to the curve passing through the point X. Conversely, at any point R on the curve C, let T be the tangent line at that point R; then there is a unique point X on the tangent T which forms with the pedal point P a line perpendicular to the tangent T – the pedal curve is the set of such points X, called the foot of the perpendicular to the tangent T from the fixed point P, as the variable point R ranges over the curve C.

Projectile motion is a form of motion experienced by an object or particle that is projected in a gravitational field, such as from Earth's surface, and moves along a curved path under the action of gravity only. In the particular case of projectile motion on Earth, most calculations assume the effects of air resistance are passive and negligible. The curved path of objects in projectile motion was shown by Galileo to be a parabola, but may also be a straight line in the special case when it is thrown directly upward or downward. The study of such motions is called ballistics, and such a trajectory is a ballistic trajectory. The only force of mathematical significance that is actively exerted on the object is gravity, which acts downward, thus imparting to the object a downward acceleration towards the Earth’s center of mass. Because of the object's inertia, no external force is needed to maintain the horizontal velocity component of the object's motion. Taking other forces into account, such as aerodynamic drag or internal propulsion, requires additional analysis. A ballistic missile is a missile only guided during the relatively brief initial powered phase of flight, and whose remaining course is governed by the laws of classical mechanics.

In geometry, a straight line, usually abbreviated line, is an infinitely long object with no width, depth, or curvature, an idealization of such physical objects as a straightedge, a taut string, or a ray of light. Lines are spaces of dimension one, which may be embedded in spaces of dimension two, three, or higher. The word line may also refer, in everyday life, to a line segment, which is a part of a line delimited by two points.
In geometry, the circumscribed circle or circumcircle of a triangle is a circle that passes through all three vertices. The center of this circle is called the circumcenter of the triangle, and its radius is called the circumradius. The circumcenter is the point of intersection between the three perpendicular bisectors of the triangle's sides, and is a triangle center.
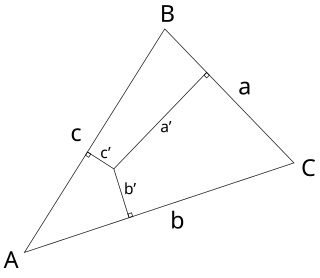
In geometry, the trilinear coordinatesx : y : z of a point relative to a given triangle describe the relative directed distances from the three sidelines of the triangle. Trilinear coordinates are an example of homogeneous coordinates. The ratio x : y is the ratio of the perpendicular distances from the point to the sides opposite vertices A and B respectively; the ratio y : z is the ratio of the perpendicular distances from the point to the sidelines opposite vertices B and C respectively; and likewise for z : x and vertices C and A.
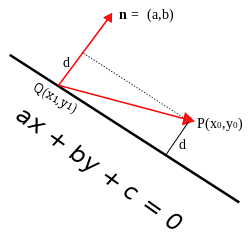
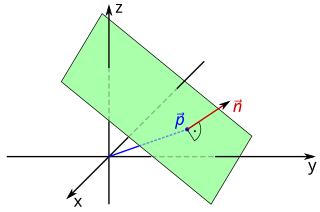
In Euclidean space, the distance from a point to a plane is the distance between a given point and its orthogonal projection on the plane, the perpendicular distance to the nearest point on the plane.
In Euclidean plane geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior. Tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs. Since the tangent line to a circle at a point P is perpendicular to the radius to that point, theorems involving tangent lines often involve radial lines and orthogonal circles.

In the geometry of curves, an orthoptic is the set of points for which two tangents of a given curve meet at a right angle.
The distance between two parallel lines in the plane is the minimum distance between any two points.