
The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. It is a key result in quantum mechanics, and its discovery was a significant landmark in the development of the subject. The equation is named after Erwin Schrödinger, who postulated the equation in 1925, and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933.

In physics, a wave packet is a short "burst" or "envelope" of localized wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere constructively only over a small region of space, and destructively elsewhere. Each component wave function, and hence the wave packet, are solutions of a wave equation. Depending on the wave equation, the wave packet's profile may remain constant or it may change (dispersion) while propagating.

In particle physics, Fermi's interaction is an explanation of the beta decay, proposed by Enrico Fermi in 1933. The theory posits four fermions directly interacting with one another. This interaction explains beta decay of a neutron by direct coupling of a neutron with an electron, a neutrino and a proton.
In theoretical physics, the Rarita–Schwinger equation is the relativistic field equation of spin-3/2 fermions. It is similar to the Dirac equation for spin-1/2 fermions. This equation was first introduced by William Rarita and Julian Schwinger in 1941.
In differential geometry, the four-gradient is the four-vector analogue of the gradient from vector calculus.
In general relativity, the Newtonian gauge is a perturbed form of the Friedmann–Lemaître–Robertson–Walker line element. The gauge freedom of general relativity is used to eliminate two scalar degrees of freedom of the metric, so that it can be written as:
In physics and fluid mechanics, a Blasius boundary layer describes the steady two-dimensional laminar boundary layer that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow. Falkner and Skan later generalized Blasius' solution to wedge flow, i.e. flows in which the plate is not parallel to the flow.

Lattice Boltzmann methods (LBM), originated from the lattice gas automata (LGA) method, is a class of computational fluid dynamics (CFD) methods for fluid simulation. Instead of solving the Navier–Stokes equations directly, a fluid density on a lattice is simulated with streaming and collision (relaxation) processes. The method is versatile as the model fluid can straightforwardly be made to mimic common fluid behaviour like vapour/liquid coexistence, and so fluid systems such as liquid droplets can be simulated. Also, fluids in complex environments such as porous media can be straightforwardly simulated, whereas with complex boundaries other CFD methods can be hard to work with.
The Poisson–Boltzmann equation is a useful equation in many settings, whether it be to understand physiological interfaces, polymer science, electron interactions in a semiconductor, or more. It aims to describe the distribution of the electric potential in solution in the direction normal to a charged surface. This distribution is important to determine how the electrostatic interactions will affect the molecules in solution. The Poisson–Boltzmann equation is derived via mean-field assumptions. From the Poisson–Boltzmann equation many other equations have been derived with a number of different assumptions.

The Newman–Penrose (NP) formalism is a set of notation developed by Ezra T. Newman and Roger Penrose for general relativity (GR). Their notation is an effort to treat general relativity in terms of spinor notation, which introduces complex forms of the usual variables used in GR. The NP formalism is itself a special case of the tetrad formalism, where the tensors of the theory are projected onto a complete vector basis at each point in spacetime. Usually this vector basis is chosen to reflect some symmetry of the spacetime, leading to simplified expressions for physical observables. In the case of the NP formalism, the vector basis chosen is a null tetrad: a set of four null vectors—two real, and a complex-conjugate pair. The two real members asymptotically point radially inward and radially outward, and the formalism is well adapted to treatment of the propagation of radiation in curved spacetime. The Weyl scalars, derived from the Weyl tensor, are often used. In particular, it can be shown that one of these scalars— in the appropriate frame—encodes the outgoing gravitational radiation of an asymptotically flat system.
In the Newman–Penrose (NP) formalism of general relativity, Weyl scalars refer to a set of five complex scalars which encode the ten independent components of the Weyl tensor of a four-dimensional spacetime.
In many-body theory, the term Green's function is sometimes used interchangeably with correlation function, but refers specifically to correlators of field operators or creation and annihilation operators.
In physics, X-waves are localized solutions of the wave equation that travel at a constant velocity in a given direction. X-waves can be sound, electromagnetic, or gravitational waves. They are built as a non-monochromatic superposition of Bessel beams. Ideal X-waves carry infinite energy, but finite-energy realizations have been observed in various frameworks. Electromagnetic X-waves travel faster than the speed of light, and X-wave pulses can have superluminal phase and group velocity.
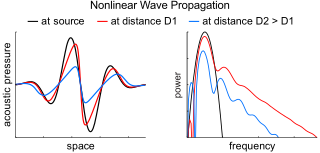
Nonlinear acoustics (NLA) is a branch of physics and acoustics dealing with sound waves of sufficiently large amplitudes. Large amplitudes require using full systems of governing equations of fluid dynamics and elasticity. These equations are generally nonlinear, and their traditional linearization is no longer possible. The solutions of these equations show that, due to the effects of nonlinearity, sound waves are being distorted as they travel.
The intent of this article is to highlight the important points of the derivation of the Navier–Stokes equations as well as its application and formulation for different families of fluids.
In mathematics – specifically, in stochastic analysis – an Itô diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation used in physics to describe the Brownian motion of a particle subjected to a potential in a viscous fluid. Itô diffusions are named after the Japanese mathematician Kiyosi Itô.
In quantum mechanics, and especially quantum information theory, the purity of a normalized quantum state is a scalar defined as
In quantum mechanics, universality is the observation that there are properties for a large class of systems that are independent of the exact structural details of the system. The notion of universality is familiar in the study and application of statistical mechanics to various physical systems since its introduction in a very precise fashion by Leo Kadanoff. Although not quite the same, it is closely related to universality as applied to quantum systems. This concept links to the essence of renormalization and scaling in many problems. Renormalization is based on the notion that a measurement device of wavelength is insensitive to details of structure at distances much smaller than . An important consequence of universality is that one can mimic the real short-structure distance of the measurement device and the system to be measured by simple short-distance structure. Even though it is seen that scaling, universality and renormalization are closely related, they are not to be used interchangeably.
In physics and mathematics, the spacetime triangle diagram (STTD) technique, also known as the Smirnov method of incomplete separation of variables, is the direct space-time domain method for electromagnetic and scalar wave motion.
Tau functions are an important ingredient in the modern theory of integrable systems, and have numerous applications in a variety of other domains. They were originally introduced by Ryogo Hirota in his direct method approach to soliton equations, based on expressing them in an equivalent bilinear form. The term Tau function, or -function, was first used systematically by Mikio Sato and his students in the specific context of the Kadomtsev–Petviashvili equation, and related integrable hierarchies. It is a central ingredient in the theory of solitons. Tau functions also appear as matrix model partition functions in the spectral theory of Random Matrices, and may also serve as generating functions, in the sense of combinatorics and enumerative geometry, especially in relation to moduli spaces of Riemann surfaces, and enumeration of branched coverings, or so-called Hurwitz numbers.







