This article appears to be a dictionary definition .(June 2023) |
Effective range is a term with several definitions depending upon context.
This article appears to be a dictionary definition .(June 2023) |
Effective range is a term with several definitions depending upon context.
Effective range may describe a distance between two points where one point is subject to an energy release at the other point. The source, receiver, and conditions between the two points must be specified to define an effective range. Effective range may represent the maximum distance at which a measuring device or receiver will predictably respond to an energy release of specified magnitude. Alternatively, effective range may be the maximum distance at which the energy released from a specified device will cause the desired effect on a target receiver. Angular dispersion may be significant to effectiveness for asymmetrical energy propagation toward small targets.
The following definition has been attributed to the United States Department of Defense: The maximum distance at which a weapon may be expected to be accurate and achieve the desired effect. [1] Accuracy is ambiguous in the absence of a specified hit probability per unit of ammunition; and for any given weapon, the desired effect could be interpreted differently depending upon the target. Subjective interpretation of these variables has caused endless and heated debate for more than a century. [2]
This section may contain material not related to the topic of the article .(May 2024) |
With the addition of clinometers fixed machine gun squads could set long ranges and deliver plunging fire or indirect fire at more than 2,500 m (2,730 yd). This indirect firing method exploits the maximal practical range, that is defined by the maximum range of a small-arms projectile while still maintaining the minimum kinetic energy required to put unprotected personnel out of action, which is generally believed to be 15 kilogram-meters (147 J / 108 ft⋅lbf). [3] Advanced planned and unplanned map and range table predicted support/harassment firing methods developed during World War I like plunging fire or indirect fire were not as commonly used by machine gunners during World War II and later as they were during World War I. [4]
In a broader context, effective range describes the distance a vehicle (including weapon launch platforms like a ship or aircraft) may be expected to deliver a specified payload from a base or refueling point. [5]
In statistics, range refers to the difference between the largest and smallest value of a set of quantified observations. Some observers consider it appropriate to remove unusually high or low outlying values to narrow the observed range to an effective range of the quantity being observed. Inferences based on effective range are of somewhat doubtful value if subjective judgement is used to determine which observations are discarded. [6]
This section may be confusing or unclear to readers. In particular, most symbols in the formulae are unexplained. What is the length to do with the potential?.(February 2020) |
In nuclear physics research, effective range is a physical parameter in the dimension of length to characterize an effective scattering square well potential. It is related to the scattering phase shift by,
. [7]
where is defined by the relation of deuteron binding energy .
In the limit of zero energy (), the scattering length can be related to effective length with .

The Diesel cycle is a combustion process of a reciprocating internal combustion engine. In it, fuel is ignited by heat generated during the compression of air in the combustion chamber, into which fuel is then injected. This is in contrast to igniting the fuel-air mixture with a spark plug as in the Otto cycle (four-stroke/petrol) engine. Diesel engines are used in aircraft, automobiles, power generation, diesel–electric locomotives, and both surface ships and submarines.

In electrical engineering, a transmission line is a specialized cable or other structure designed to conduct electromagnetic waves in a contained manner. The term applies when the conductors are long enough that the wave nature of the transmission must be taken into account. This applies especially to radio-frequency engineering because the short wavelengths mean that wave phenomena arise over very short distances. However, the theory of transmission lines was historically developed to explain phenomena on very long telegraph lines, especially submarine telegraph cables.

Ionization is the process by which an atom or a molecule acquires a negative or positive charge by gaining or losing electrons, often in conjunction with other chemical changes. The resulting electrically charged atom or molecule is called an ion. Ionization can result from the loss of an electron after collisions with subatomic particles, collisions with other atoms, molecules and ions, or through the interaction with electromagnetic radiation. Heterolytic bond cleavage and heterolytic substitution reactions can result in the formation of ion pairs. Ionization can occur through radioactive decay by the internal conversion process, in which an excited nucleus transfers its energy to one of the inner-shell electrons causing it to be ejected.

An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics. The requirement of zero interaction can often be relaxed if, for example, the interaction is perfectly elastic or regarded as point-like collisions.

In complex analysis, the residue theorem, sometimes called Cauchy's residue theorem, is a powerful tool to evaluate line integrals of analytic functions over closed curves; it can often be used to compute real integrals and infinite series as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula. The residue theorem should not be confused with special cases of the generalized Stokes' theorem; however, the latter can be used as an ingredient of its proof.

In mathematics, the digamma function is defined as the logarithmic derivative of the gamma function:

In particle physics, the Klein–Nishina formula gives the differential cross section of photons scattered from a single free electron, calculated in the lowest order of quantum electrodynamics. It was first derived in 1928 by Oskar Klein and Yoshio Nishina, constituting one of the first successful applications of the Dirac equation. The formula describes both the Thomson scattering of low energy photons and the Compton scattering of high energy photons, showing that the total cross section and expected deflection angle decrease with increasing photon energy.
In quantum physics, the scattering amplitude is the probability amplitude of the outgoing spherical wave relative to the incoming plane wave in a stationary-state scattering process. At large distances from the centrally symmetric scattering center, the plane wave is described by the wavefunction

The bulk modulus of a substance is a measure of the resistance of a substance to bulk compression. It is defined as the ratio of the infinitesimal pressure increase to the resulting relative decrease of the volume.
In mathematics, the discrete Laplace operator is an analog of the continuous Laplace operator, defined so that it has meaning on a graph or a discrete grid. For the case of a finite-dimensional graph, the discrete Laplace operator is more commonly called the Laplacian matrix.
Scattering parameters or S-parameters describe the electrical behavior of linear electrical networks when undergoing various steady state stimuli by electrical signals.
In physics, the optical theorem is a general law of wave scattering theory, which relates the zero-angle scattering amplitude to the total cross section of the scatterer. It is usually written in the form

Electron scattering occurs when electrons are displaced from their original trajectory. This is due to the electrostatic forces within matter interaction or, if an external magnetic field is present, the electron may be deflected by the Lorentz force. This scattering typically happens with solids such as metals, semiconductors and insulators; and is a limiting factor in integrated circuits and transistors.

In quantum electrodynamics, Bhabha scattering is the electron-positron scattering process:
The plasma parameter is a dimensionless number, denoted by capital Lambda, Λ. The plasma parameter is usually interpreted to be the argument of the Coulomb logarithm, which is the ratio of the maximum impact parameter to the classical distance of closest approach in Coulomb scattering. In this case, the plasma parameter is given by:
Intrabeam scattering (IBS) is an effect in accelerator physics where collisions between particles couple the beam emittance in all three dimensions. This generally causes the beam size to grow. In proton accelerators, intrabeam scattering causes the beam to grow slowly over a period of several hours. This limits the luminosity lifetime. In circular lepton accelerators, intrabeam scattering is counteracted by radiation damping, resulting in a new equilibrium beam emittance with a relaxation time on the order of milliseconds. Intrabeam scattering creates an inverse relationship between the smallness of the beam and the number of particles it contains, therefore limiting luminosity.
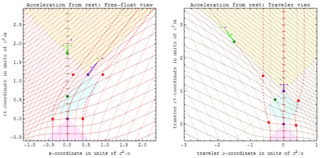
In relativity theory, proper acceleration is the physical acceleration experienced by an object. It is thus acceleration relative to a free-fall, or inertial, observer who is momentarily at rest relative to the object being measured. Gravitation therefore does not cause proper acceleration, because the same gravity acts equally on the inertial observer. As a consequence, all inertial observers always have a proper acceleration of zero.
The air mass coefficient defines the direct optical path length through the Earth's atmosphere, expressed as a ratio relative to the path length vertically upwards, i.e. at the zenith. The air mass coefficient can be used to help characterize the solar spectrum after solar radiation has traveled through the atmosphere.
In mathematics, the Möbius energy of a knot is a particular knot energy, i.e., a functional on the space of knots. It was discovered by Jun O'Hara, who demonstrated that the energy blows up as the knot's strands get close to one another. This is a useful property because it prevents self-intersection and ensures the result under gradient descent is of the same knot type.
Isentropic nozzle flow describes the movement of a gas or fluid through a narrowing opening without an increase or decrease in entropy.