
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun. The laws modified the heliocentric theory of Nicolaus Copernicus, replacing its circular orbits and epicycles with elliptical trajectories, and explaining how planetary velocities vary. The three laws state that:
- The orbit of a planet is an ellipse with the Sun at one of the two foci.
- A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
- The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit.

In celestial mechanics, an orbit is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such as a planet, moon, asteroid, or Lagrange point. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion.
Orbital elements are the parameters required to uniquely identify a specific orbit. In celestial mechanics these elements are considered in two-body systems using a Kepler orbit. There are many different ways to mathematically describe the same orbit, but certain schemes, each consisting of a set of six parameters, are commonly used in astronomy and orbital mechanics.

Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets, satellites, and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and the law of universal gravitation. Orbital mechanics is a core discipline within space-mission design and control.

The equation of time describes the discrepancy between two kinds of solar time. The word equation is used in the medieval sense of "reconciliation of a difference". The two times that differ are the apparent solar time, which directly tracks the diurnal motion of the Sun, and mean solar time, which tracks a theoretical mean Sun with uniform motion along the celestial equator. Apparent solar time can be obtained by measurement of the current position of the Sun, as indicated by a sundial. Mean solar time, for the same place, would be the time indicated by a steady clock set so that over the year its differences from apparent solar time would have a mean of zero.
In classical mechanics, the Laplace–Runge–Lenz (LRL) vector is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be conserved. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems.
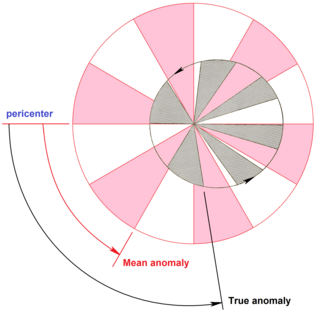
In celestial mechanics, the mean anomaly is the fraction of an elliptical orbit's period that has elapsed since the orbiting body passed periapsis, expressed as an angle which can be used in calculating the position of that body in the classical two-body problem. It is the angular distance from the pericenter which a fictitious body would have if it moved in a circular orbit, with constant speed, in the same orbital period as the actual body in its elliptical orbit.
In orbital mechanics, the eccentric anomaly is an angular parameter that defines the position of a body that is moving along an elliptic Kepler orbit. The eccentric anomaly is one of three angular parameters ("anomalies") that define a position along an orbit, the other two being the true anomaly and the mean anomaly.

In celestial mechanics, true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse.

In astrodynamics or celestial mechanics a parabolic trajectory is a Kepler orbit with the eccentricity equal to 1 and is an unbound orbit that is exactly on the border between elliptical and hyperbolic. When moving away from the source it is called an escape orbit, otherwise a capture orbit. It is also sometimes referred to as a C3 = 0 orbit (see Characteristic energy).

In astrodynamics or celestial mechanics, a hyperbolic trajectory or hyperbolic orbit is the trajectory of any object around a central body with more than enough speed to escape the central object's gravitational pull. The name derives from the fact that according to Newtonian theory such an orbit has the shape of a hyperbola. In more technical terms this can be expressed by the condition that the orbital eccentricity is greater than one.

In astrodynamics or celestial mechanics, an elliptic orbit or elliptical orbit is a Kepler orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1. In a wider sense, it is a Kepler orbit with negative energy. This includes the radial elliptic orbit, with eccentricity equal to 1.
In orbital mechanics, mean motion is the angular speed required for a body to complete one orbit, assuming constant speed in a circular orbit which completes in the same time as the variable speed, elliptical orbit of the actual body. The concept applies equally well to a small body revolving about a large, massive primary body or to two relatively same-sized bodies revolving about a common center of mass. While nominally a mean, and theoretically so in the case of two-body motion, in practice the mean motion is not typically an average over time for the orbits of real bodies, which only approximate the two-body assumption. It is rather the instantaneous value which satisfies the above conditions as calculated from the current gravitational and geometric circumstances of the body's constantly-changing, perturbed orbit.
In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force F that varies in strength as the inverse square of the distance r between them. The force may be either attractive or repulsive. The problem is to find the position or speed of the two bodies over time given their masses, positions, and velocities. Using classical mechanics, the solution can be expressed as a Kepler orbit using six orbital elements.
In mathematics, the Laplace limit is the maximum value of the eccentricity for which a solution to Kepler's equation, in terms of a power series in the eccentricity, converges. It is approximately

In celestial mechanics, a Kepler orbit is the motion of one body relative to another, as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space. A Kepler orbit can also form a straight line. It considers only the point-like gravitational attraction of two bodies, neglecting perturbations due to gravitational interactions with other objects, atmospheric drag, solar radiation pressure, a non-spherical central body, and so on. It is thus said to be a solution of a special case of the two-body problem, known as the Kepler problem. As a theory in classical mechanics, it also does not take into account the effects of general relativity. Keplerian orbits can be parametrized into six orbital elements in various ways.
In orbital mechanics, the universal variable formulation is a method used to solve the two-body Kepler problem. It is a generalized form of Kepler's Equation, extending them to apply not only to elliptic orbits, but also parabolic and hyperbolic orbits. It thus is applicable to many situations in the Solar System, where orbits of widely varying eccentricities are present.
In celestial mechanics, Lambert's problem is concerned with the determination of an orbit from two position vectors and the time of flight, posed in the 18th century by Johann Heinrich Lambert and formally solved with mathematical proof by Joseph-Louis Lagrange. It has important applications in the areas of rendezvous, targeting, guidance, and preliminary orbit determination.
In astrodynamics and celestial mechanics a radial trajectory is a Kepler orbit with zero angular momentum. Two objects in a radial trajectory move directly towards or away from each other in a straight line.
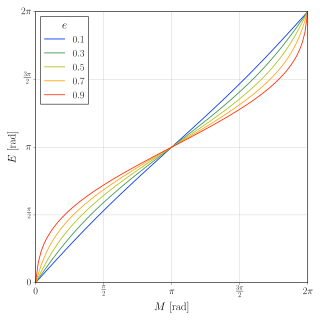
In orbital mechanics, Kepler's equation relates various geometric properties of the orbit of a body subject to a central force.




















