Related Research Articles
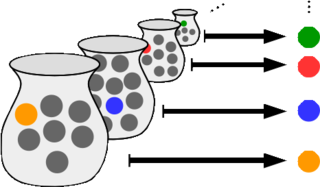
In mathematics, the axiom of choice, or AC, is an axiom of set theory equivalent to the statement that a Cartesian product of a collection of non-empty sets is non-empty. Informally put, the axiom of choice says that given any collection of sets, each containing at least one element, it is possible to construct a new set by arbitrarily choosing one element from each set, even if the collection is infinite. Formally, it states that for every indexed family of nonempty sets, there exists an indexed set such that for every . The axiom of choice was formulated in 1904 by Ernst Zermelo in order to formalize his proof of the well-ordering theorem.
In mathematics, the axiom of regularity is an axiom of Zermelo–Fraenkel set theory that states that every non-empty set A contains an element that is disjoint from A. In first-order logic, the axiom reads:
In mathematics, specifically set theory, the continuum hypothesis is a hypothesis about the possible sizes of infinite sets. It states that
there is no set whose cardinality is strictly between that of the integers and the real numbers,

Gödel's completeness theorem is a fundamental theorem in mathematical logic that establishes a correspondence between semantic truth and syntactic provability in first-order logic.
Mathematical logic is the study of formal logic within mathematics. Major subareas include model theory, proof theory, set theory, and recursion theory. Research in mathematical logic commonly addresses the mathematical properties of formal systems of logic such as their expressive or deductive power. However, it can also include uses of logic to characterize correct mathematical reasoning or to establish foundations of mathematics.
In mathematics, the well-ordering theorem, also known as Zermelo's theorem, states that every set can be well-ordered. A set X is well-ordered by a strict total order if every non-empty subset of X has a least element under the ordering. The well-ordering theorem together with Zorn's lemma are the most important mathematical statements that are equivalent to the axiom of choice. Ernst Zermelo introduced the axiom of choice as an "unobjectionable logical principle" to prove the well-ordering theorem. One can conclude from the well-ordering theorem that every set is susceptible to transfinite induction, which is considered by mathematicians to be a powerful technique. One famous consequence of the theorem is the Banach–Tarski paradox.

Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory. It states that a partially ordered set containing upper bounds for every chain necessarily contains at least one maximal element.
Gödel's incompleteness theorems are two theorems of mathematical logic that are concerned with the limits of provability in formal axiomatic theories. These results, published by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of mathematics. The theorems are widely, but not universally, interpreted as showing that Hilbert's program to find a complete and consistent set of axioms for all mathematics is impossible.
In classical deductive logic, a consistent theory is one that does not lead to a logical contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if it has a model, i.e., there exists an interpretation under which all formulas in the theory are true. This is the sense used in traditional Aristotelian logic, although in contemporary mathematical logic the term satisfiable is used instead. The syntactic definition states a theory is consistent if there is no formula such that both and its negation are elements of the set of consequences of . Let be a set of closed sentences and the set of closed sentences provable from under some formal deductive system. The set of axioms is consistent when for no formula .
In set theory, Zermelo–Fraenkel set theory, named after mathematicians Ernst Zermelo and Abraham Fraenkel, is an axiomatic system that was proposed in the early twentieth century in order to formulate a theory of sets free of paradoxes such as Russell's paradox. Today, Zermelo–Fraenkel set theory, with the historically controversial axiom of choice (AC) included, is the standard form of axiomatic set theory and as such is the most common foundation of mathematics. Zermelo–Fraenkel set theory with the axiom of choice included is abbreviated ZFC, where C stands for "choice", and ZF refers to the axioms of Zermelo–Fraenkel set theory with the axiom of choice excluded.

Metamathematics is the study of mathematics itself using mathematical methods. This study produces metatheories, which are mathematical theories about other mathematical theories. Emphasis on metamathematics owes itself to David Hilbert's attempt to secure the foundations of mathematics in the early part of the 20th century. Metamathematics provides "a rigorous mathematical technique for investigating a great variety of foundation problems for mathematics and logic". An important feature of metamathematics is its emphasis on differentiating between reasoning from inside a system and from outside a system. An informal illustration of this is categorizing the proposition "2+2=4" as belonging to mathematics while categorizing the proposition "'2+2=4' is valid" as belonging to metamathematics.
In mathematics, the Boolean prime ideal theorem states that ideals in a Boolean algebra can be extended to prime ideals. A variation of this statement for filters on sets is known as the ultrafilter lemma. Other theorems are obtained by considering different mathematical structures with appropriate notions of ideals, for example, rings and prime ideals, or distributive lattices and maximal ideals. This article focuses on prime ideal theorems from order theory.
Reverse mathematics is a program in mathematical logic that seeks to determine which axioms are required to prove theorems of mathematics. Its defining method can briefly be described as "going backwards from the theorems to the axioms", in contrast to the ordinary mathematical practice of deriving theorems from axioms. It can be conceptualized as sculpting out necessary conditions from sufficient ones.
In mathematics, the axiom of dependent choice, denoted by , is a weak form of the axiom of choice that is still sufficient to develop most of real analysis. It was introduced by Paul Bernays in a 1942 article that explores which set-theoretic axioms are needed to develop analysis.
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted by V, is the class of hereditary well-founded sets. This collection, which is formalized by Zermelo–Fraenkel set theory (ZFC), is often used to provide an interpretation or motivation of the axioms of ZFC. The concept is named after John von Neumann, although it was first published by Ernst Zermelo in 1930.
In the foundations of mathematics, von Neumann–Bernays–Gödel set theory (NBG) is an axiomatic set theory that is a conservative extension of Zermelo–Fraenkel–choice set theory (ZFC). NBG introduces the notion of class, which is a collection of sets defined by a formula whose quantifiers range only over sets. NBG can define classes that are larger than sets, such as the class of all sets and the class of all ordinals. Morse–Kelley set theory (MK) allows classes to be defined by formulas whose quantifiers range over classes. NBG is finitely axiomatizable, while ZFC and MK are not.
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is proved to be impossible to construct an algorithm that always leads to a correct yes-or-no answer. The halting problem is an example: it can be proven that there is no algorithm that correctly determines whether arbitrary programs eventually halt when run.
Jean Estelle Hirsh Rubin was an American mathematician known for her research on the axiom of choice. She worked for many years as a professor of mathematics at Purdue University. Rubin wrote five books: three on the axiom of choice, and two more on more general topics in set theory and mathematical logic.
References
- 1 2 Goodstein, R. L. (October 1964), "Review of Equivalents of the Axiom of Choice", The Mathematical Gazette , 48 (365): 348, doi:10.2307/3613069, JSTOR 3613069
- 1 2 3 4 Smith, Perry (1987), "Review of Equivalents of the Axiom of Choice, II", Mathematical Reviews , MR 0798475
- 1 2 3 Chang, C.-C., "Review of Equivalents of the Axiom of Choice", Mathematical Reviews , MR 0153590
- 1 2 Plotkin, J. M., "Review of Equivalents of the Axiom of Choice, II", zbMATH , Zbl 0582.03033
- ↑ Pincus, David (September 1987), "Review of Equivalents of the Axiom of Choice, II", Journal of Symbolic Logic , 52 (3): 867–869, doi:10.2307/2274372, JSTOR 2274372