
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction (EDAC) or error control are techniques that enable reliable delivery of digital data over unreliable communication channels. Many communication channels are subject to channel noise, and thus errors may be introduced during transmission from the source to a receiver. Error detection techniques allow detecting such errors, while error correction enables reconstruction of the original data in many cases.
In telecommunication, a convolutional code is a type of error-correcting code that generates parity symbols via the sliding application of a boolean polynomial function to a data stream. The sliding application represents the 'convolution' of the encoder over the data, which gives rise to the term 'convolutional coding'. The sliding nature of the convolutional codes facilitates trellis decoding using a time-invariant trellis. Time invariant trellis decoding allows convolutional codes to be maximum-likelihood soft-decision decoded with reasonable complexity.
Reed–Solomon codes are a group of error-correcting codes that were introduced by Irving S. Reed and Gustave Solomon in 1960. They have many applications, including consumer technologies such as MiniDiscs, CDs, DVDs, Blu-ray discs, QR codes, Data Matrix, data transmission technologies such as DSL and WiMAX, broadcast systems such as satellite communications, DVB and ATSC, and storage systems such as RAID 6.

Arithmetic coding (AC) is a form of entropy encoding used in lossless data compression. Normally, a string of characters is represented using a fixed number of bits per character, as in the ASCII code. When a string is converted to arithmetic encoding, frequently used characters will be stored with fewer bits and not-so-frequently occurring characters will be stored with more bits, resulting in fewer bits used in total. Arithmetic coding differs from other forms of entropy encoding, such as Huffman coding, in that rather than separating the input into component symbols and replacing each with a code, arithmetic coding encodes the entire message into a single number, an arbitrary-precision fraction q, where 0.0 ≤ q < 1.0. It represents the current information as a range, defined by two numbers. A recent family of entropy coders called asymmetric numeral systems allows for faster implementations thanks to directly operating on a single natural number representing the current information.

Coding theory is the study of the properties of codes and their respective fitness for specific applications. Codes are used for data compression, cryptography, error detection and correction, data transmission and data storage. Codes are studied by various scientific disciplines—such as information theory, electrical engineering, mathematics, linguistics, and computer science—for the purpose of designing efficient and reliable data transmission methods. This typically involves the removal of redundancy and the correction or detection of errors in the transmitted data.
In information theory, turbo codes are a class of high-performance forward error correction (FEC) codes developed around 1990–91, but first published in 1993. They were the first practical codes to closely approach the maximum channel capacity or Shannon limit, a theoretical maximum for the code rate at which reliable communication is still possible given a specific noise level. Turbo codes are used in 3G/4G mobile communications and in satellite communications as well as other applications where designers seek to achieve reliable information transfer over bandwidth- or latency-constrained communication links in the presence of data-corrupting noise. Turbo codes compete with low-density parity-check (LDPC) codes, which provide similar performance.
In information theory, a low-density parity-check (LDPC) code is a linear error correcting code, a method of transmitting a message over a noisy transmission channel. An LDPC code is constructed using a sparse Tanner graph. LDPC codes are capacity-approaching codes, which means that practical constructions exist that allow the noise threshold to be set very close to the theoretical maximum for a symmetric memoryless channel. The noise threshold defines an upper bound for the channel noise, up to which the probability of lost information can be made as small as desired. Using iterative belief propagation techniques, LDPC codes can be decoded in time linear in their block length.

A QR code is a type of two-dimensional matrix barcode, invented in 1994, by Japanese company Denso Wave for labelling automobile parts. A QR code consists of black squares arranged in a square grid on a white background, including some fiducial markers, which can be read by an imaging device, such as a camera, and processed using Reed–Solomon error correction until the image can be appropriately interpreted. The required data are then extracted from patterns that are present in both the horizontal and the vertical components of the QR image.
In coding theory, block codes are a large and important family of error-correcting codes that encode data in blocks. There is a vast number of examples for block codes, many of which have a wide range of practical applications. The abstract definition of block codes is conceptually useful because it allows coding theorists, mathematicians, and computer scientists to study the limitations of all block codes in a unified way. Such limitations often take the form of bounds that relate different parameters of the block code to each other, such as its rate and its ability to detect and correct errors.

A Data Matrix is a two-dimensional code consisting of black and white "cells" or dots arranged in either a square or rectangular pattern, also known as a matrix. The information to be encoded can be text or numeric data. Usual data size is from a few bytes up to 1556 bytes. The length of the encoded data depends on the number of cells in the matrix. Error correction codes are often used to increase reliability: even if one or more cells are damaged so it is unreadable, the message can still be read. A Data Matrix symbol can store up to 2,335 alphanumeric characters.
In computer science, Luby transform codes are the first class of practical fountain codes that are near-optimal erasure correcting codes. They were invented by Michael Luby in 1998 and published in 2002. Like some other fountain codes, LT codes depend on sparse bipartite graphs to trade reception overhead for encoding and decoding speed. The distinguishing characteristic of LT codes is in employing a particularly simple algorithm based on the exclusive or operation to encode and decode the message.
In coding theory, fountain codes are a class of erasure codes with the property that a potentially limitless sequence of encoding symbols can be generated from a given set of source symbols such that the original source symbols can ideally be recovered from any subset of the encoding symbols of size equal to or only slightly larger than the number of source symbols. The term fountain or rateless refers to the fact that these codes do not exhibit a fixed code rate.
In coding theory, the repetition code is one of the most basic linear error-correcting codes. In order to transmit a message over a noisy channel that may corrupt the transmission in a few places, the idea of the repetition code is to just repeat the message several times. The hope is that the channel corrupts only a minority of these repetitions. This way the receiver will notice that a transmission error occurred since the received data stream is not the repetition of a single message, and moreover, the receiver can recover the original message by looking at the received message in the data stream that occurs most often.
In computing, telecommunication, information theory, and coding theory, forward error correction (FEC) or channel coding is a technique used for controlling errors in data transmission over unreliable or noisy communication channels.
In computer storage, the standard RAID levels comprise a basic set of RAID configurations that employ the techniques of striping, mirroring, or parity to create large reliable data stores from multiple general-purpose computer hard disk drives (HDDs). The most common types are RAID 0 (striping), RAID 1 (mirroring) and its variants, RAID 5, and RAID 6. Multiple RAID levels can also be combined or nested, for instance RAID 10 or RAID 01. RAID levels and their associated data formats are standardized by the Storage Networking Industry Association (SNIA) in the Common RAID Disk Drive Format (DDF) standard. The numerical values only serve as identifiers and do not signify performance, reliability, generation, or any other metric.
In coding theory, a systematic code is any error-correcting code in which the input data are embedded in the encoded output. Conversely, in a non-systematic code the output does not contain the input symbols.
In coding theory, concatenated codes form a class of error-correcting codes that are derived by combining an inner code and an outer code. They were conceived in 1966 by Dave Forney as a solution to the problem of finding a code that has both exponentially decreasing error probability with increasing block length and polynomial-time decoding complexity. Concatenated codes became widely used in space communications in the 1970s.
In coding theory, folded Reed–Solomon codes are like Reed–Solomon codes, which are obtained by mapping Reed–Solomon codewords over a larger alphabet by careful bundling of codeword symbols.
In coding theory, burst error-correcting codes employ methods of correcting burst errors, which are errors that occur in many consecutive bits rather than occurring in bits independently of each other.
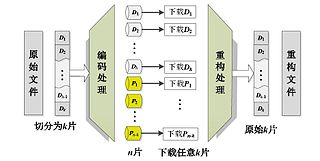
Binary Reed–Solomon coding (BRS), which belongs to a RS code, is a way of encoding that can fix node data loss in a distributed storage environment. It has maximum distance separable (MDS) encoding properties. Its encoding and decoding rate outperforms conventional RS coding and optimum CRS coding.
















