
In geometry, a subset of a Euclidean space, or more generally an affine space over the reals, is convex if, given any two points, it contains the whole line segment that joins them. Equivalently, a convex set or a convex region is a subset that intersect every line into a single line segment . For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex.

In geometry, a polyhedron is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices. The word polyhedron comes from the Classical Greek πολύεδρον, as poly- + -hedron.

In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset.
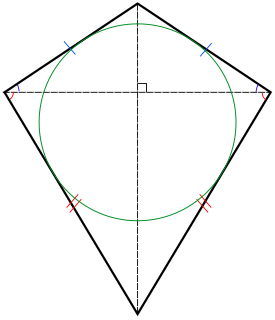
In Euclidean geometry, a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are adjacent to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite to each other instead of being adjacent. Kite quadrilaterals are named for the wind-blown, flying kites, which often have this shape and which are in turn named for a bird. Kites are also known as deltoids, but the word "deltoid" may also refer to a deltoid curve, an unrelated geometric object.

In Euclidean geometry, a convex quadrilateral with at least one pair of parallel sides is referred to as a trapezium in English outside North America, but as a trapezoid in American and Canadian English. The parallel sides are called the bases of the trapezoid and the other two sides are called the legs or the lateral sides. A scalene trapezoid is a trapezoid with no sides of equal measure, in contrast to the special cases below.
In mathematics, the isoperimetric inequality is a geometric inequality involving the perimeter of a set and its volume. In -dimensional space the inequality lower bounds the surface area or perimeter of a set by its volume ,

In hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed. As such, the Klein quartic is the Hurwitz surface of lowest possible genus; see Hurwitz's automorphisms theorem. Its (orientation-preserving) automorphism group is isomorphic to PSL(2, 7), the second-smallest non-abelian simple group. The quartic was first described in.
In mathematics, equivariance is a form of symmetry for functions from one space with symmetry to another. A function is said to be an equivariant map when its domain and codomain are acted on by the same symmetry group, and when the function commutes with the action of the group. That is, applying a symmetry transformation and then computing the function produces the same result as computing the function and then applying the transformation.

In geometry, a curve of constant width is a simple closed curve in the plane whose width is the same in all directions, regardless of the slope of the lines. The shape bounded by a curve of constant width is a body of constant width or an orbiform, the name given to these shapes by Leonhard Euler. Standard examples are the circle and the Reuleaux triangle. These curves can also be constructed using circular arcs centered at crossings of an arrangement of lines, as the involutes of certain curves, or by intersecting circles centered on a partial curve.

A Reuleaux triangle[ʁœlo] is a shape formed from the intersection of three circular disks, each having its center on the boundary of the other two. Its boundary is a curve of constant width, the simplest and best known such curve other than the circle itself. Constant width means that the separation of every two parallel supporting lines is the same, independent of their orientation. Because all its diameters are the same, the Reuleaux triangle is one answer to the question "Other than a circle, what shape can a manhole cover be made so that it cannot fall down through the hole?"

In mathematics, a Kakeya set, or Besicovitch set, is a set of points in Euclidean space which contains a unit line segment in every direction. For instance, a disk of radius 1/2 in the Euclidean plane, or a ball of radius 1/2 in three-dimensional space, forms a Kakeya set. Much of the research in this area has studied the problem of how small such sets can be. Besicovitch showed that there are Besicovitch sets of measure zero.
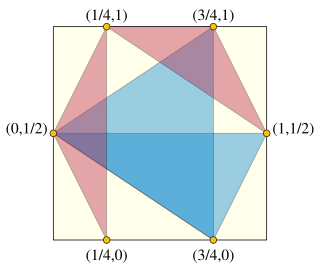
In discrete geometry and discrepancy theory, the Heilbronn triangle problem is a problem of placing points within a region in the plane, in order to avoid triangles of small area. It is named after Hans Heilbronn, who conjectured prior to 1950 that this smallest triangle area is necessarily at most inversely proportional to the square of the number of points. Heilbronn's conjecture was proven false, but the asymptotic growth rate of the minimum triangle area remains unknown.

In geometry, a pentagonal tiling is a tiling of the plane where each individual piece is in the shape of a pentagon.
Theodor Estermann was a mathematician, working in the field of analytic number theory. The Estermann measure, a measure of the central symmetry of a convex set in the Euclidean plane, is named after him.

In plane geometry the Blaschke–Lebesgue theorem states that the Reuleaux triangle has the least area of all curves of given constant width. In the form that every curve of a given width has area at least as large as the Reuleaux triangle, it is also known as the Blaschke–Lebesgue inequality. It is named after Wilhelm Blaschke and Henri Lebesgue, who published it separately in the early 20th century.
In the geometry of the Euclidean plane, axiality is a measure of how much axial symmetry a shape has. It is defined as the ratio of areas of the largest axially symmetric subset of the shape to the whole shape. Equivalently it is the largest fraction of the area of the shape that can be covered by a mirror reflection of the shape.
In geometry, a plesiohedron is a special kind of space-filling polyhedron, defined as the Voronoi cell of a symmetric Delone set. Three-dimensional Euclidean space can be completely filled by copies of any one of these shapes, with no overlaps. The resulting honeycomb will have symmetries that take any copy of the plesiohedron to any other copy.

In plane geometry the Kovner–Besicovitch measure is a number defined for any bounded convex set describing how close to being centrally symmetric it is. It is the fraction of the area of the set that can be covered by its largest centrally symmetric subset.

In differential geometry, a hedgehog or plane hedgehog is a type of plane curve, the envelope of a family of lines determined by a support function. More intuitively, sufficiently well-behaved hedgehogs are plane curves with one tangent line in each oriented direction. A projective hedgehog is a restricted type of hedgehog, defined from an anti-symmetric support function, and forms a curve with one tangent line in each direction, regardless of orientation.
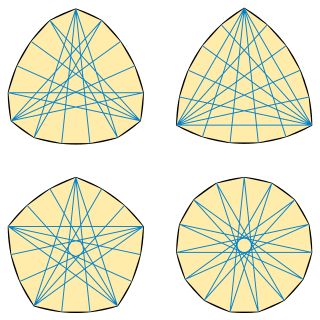
In geometry, a Reinhardt polygon is an equilateral polygon inscribed in a Reuleaux polygon. As in the regular polygons, each vertex of a Reinhardt polygon participates in at least one defining pair of the diameter of the polygon. Reinhardt polygons with sides exist, often with multiple forms, whenever is not a power of two. Among all polygons with sides, the Reinhardt polygons have the largest possible perimeter for their diameter, the largest possible width for their diameter, and the largest possible width for their perimeter. They are named after Karl Reinhardt, who studied them in 1922.
















