Related Research Articles
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. It does not assume or postulate any natural laws, but explains the macroscopic behavior of nature from the behavior of such ensembles.

The second law of thermodynamics establishes the concept of entropy as a physical property of a thermodynamic system. It can be used to predict whether processes are forbidden despite obeying the requirement of conservation of energy as expressed in the first law of thermodynamics and provides necessary criteria for spontaneous processes. The second law may be formulated by the observation that the entropy of isolated systems left to spontaneous evolution cannot decrease, as they always arrive at a state of thermodynamic equilibrium, where the entropy is highest at the given internal energy. If all processes in the system are reversible, the entropy is constant. An increase in entropy accounts for the irreversibility of natural processes, often referred to in the concept of the arrow of time.

The first law of thermodynamics is a version of the law of conservation of energy, adapted for thermodynamic processes, distinguishing three kinds of transfer of energy, as heat, as thermodynamic work, and as energy associated with matter transfer, and relating them to a function of a body's state, called internal energy.
Thermodynamic equilibrium is an axiomatic concept of thermodynamics. It is an internal state of a single thermodynamic system, or a relation between several thermodynamic systems connected by more or less permeable or impermeable walls. In thermodynamic equilibrium there are no net macroscopic flows of matter or of energy, either within a system or between systems.
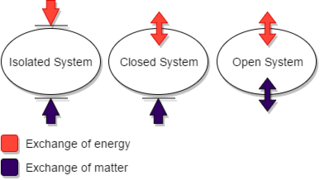
A thermodynamic system is a body of matter and/or radiation, confined in space by walls, with defined permeabilities, which separate it from its surroundings. The surroundings may include other thermodynamic systems, or physical systems that are not thermodynamic systems. A wall of a thermodynamic system may be purely notional, when it is described as being 'permeable' to all matter, all radiation, and all forces. A state of a thermodynamic system can be fully described in several different ways, by several different sets of thermodynamic state variables.

In thermodynamics, the Onsager reciprocal relations express the equality of certain ratios between flows and forces in thermodynamic systems out of equilibrium, but where a notion of local equilibrium exists.
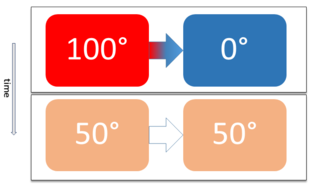
Two physical systems are in thermal equilibrium if there is no net flow of thermal energy between them when they are connected by a path permeable to heat. Thermal equilibrium obeys the zeroth law of thermodynamics. A system is said to be in thermal equilibrium with itself if the temperature within the system is spatially uniform and temporally constant.

Non-equilibrium thermodynamics is a branch of thermodynamics that deals with physical systems that are not in thermodynamic equilibrium but can be described in terms of macroscopic quantities that represent an extrapolation of the variables used to specify the system in thermodynamic equilibrium. Non-equilibrium thermodynamics is concerned with transport processes and with the rates of chemical reactions.

In science, a process that is not reversible is called irreversible. This concept arises frequently in thermodynamics. All complex natural processes are irreversible, although a phase transition at the coexistence temperature is well approximated as reversible.

The laws of thermodynamics define a group of physical quantities, such as temperature, energy, and entropy, that characterize thermodynamic systems in thermodynamic equilibrium. The laws also use various parameters for thermodynamic processes, such as thermodynamic work and heat, and establish relationships between them. They state empirical facts that form a basis of precluding the possibility of certain phenomena, such as perpetual motion. In addition to their use in thermodynamics, they are important fundamental laws of physics in general, and are applicable in other natural sciences.
The Jarzynski equality (JE) is an equation in statistical mechanics that relates free energy differences between two states and the irreversible work along an ensemble of trajectories joining the same states. It is named after the physicist Christopher Jarzynski who derived it in 1996. Fundamentally, the Jarzynski equality points to the fact that the fluctuations in the work satisfy certain constraints separately from the average value of the work that occurs in some process.
The Green–Kubo relations give the exact mathematical expression for transport coefficients in terms of integrals of time correlation functions:

In thermodynamics, a thermodynamic state of a system is its condition at a specific time; that is, fully identified by values of a suitable set of parameters known as state variables, state parameters or thermodynamic variables. Once such a set of values of thermodynamic variables has been specified for a system, the values of all thermodynamic properties of the system are uniquely determined. Usually, by default, a thermodynamic state is taken to be one of thermodynamic equilibrium. This means that the state is not merely the condition of the system at a specific time, but that the condition is the same, unchanging, over an indefinitely long duration of time.

In thermodynamics, heat is energy in transfer to or from a thermodynamic system, by mechanisms other than thermodynamic work or transfer of matter. The various mechanisms of energy transfer that define heat are stated in the next section of this article.

Diffusion is the net movement of anything generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition.
Relativistic heat conduction refers to the modelling of heat conduction in a way compatible with special relativity. This article discusses models using a wave equation with a dissipative term.
Energy dissipation and entropy production extremal principles are ideas developed within non-equilibrium thermodynamics that attempt to predict the likely steady states and dynamical structures that a physical system might show. The search for extremum principles for non-equilibrium thermodynamics follows their successful use in other branches of physics. According to Kondepudi (2008), and to Grandy (2008), there is no general rule that provides an extremum principle that governs the evolution of a far-from-equilibrium system to a steady state. According to Glansdorff and Prigogine, irreversible processes usually are not governed by global extremal principles because description of their evolution requires differential equations which are not self-adjoint, but local extremal principles can be used for local solutions. Lebon Jou and Casas-Vásquez (2008) state that "In non-equilibrium ... it is generally not possible to construct thermodynamic potentials depending on the whole set of variables". Šilhavý (1997) offers the opinion that "... the extremum principles of thermodynamics ... do not have any counterpart for [non-equilibrium] steady states ." It follows that any general extremal principle for a non-equilibrium problem will need to refer in some detail to the constraints that are specific for the structure of the system considered in the problem.
In engineering, physics and chemistry, the study of transport phenomena concerns the exchange of mass, energy, charge, momentum and angular momentum between observed and studied systems. While it draws from fields as diverse as continuum mechanics and thermodynamics, it places a heavy emphasis on the commonalities between the topics covered. Mass, momentum, and heat transport all share a very similar mathematical framework, and the parallels between them are exploited in the study of transport phenomena to draw deep mathematical connections that often provide very useful tools in the analysis of one field that are directly derived from the others.
Carlo Cattàneo was an Italian academic and one of the general relativity theorists and mathematical physicists in the 1960s and 1970s. He made contributions to general relativity theory, fluid mechanics, and elasticity theory.
Vladimir Nikolajevich Pokrovskii is a Russian scientist known for his original contributions to polymer physics and economic theory. He was the founder of the Altai school of dynamics of nonlinear fluids.
References
- ↑ Jou D, Casas-Vazquez J, Lebon G (1988), Extended irreversible thermodynamics, Rep. Prog. Phys 51 1105-1179
- ↑ Lebon G, Casas-Vazquez J, Jou D (1992), Questions and answers about a thermodynamic theory of the third type, Contemporary Phys. 33 41-51
- ↑ Müller I, Ruggeri T (1998), Rational Extended Thermodynamics, 2nd edition, Springer, New York
- ↑ Jou D, Casas-Vazquez J, Lebon G (1999), Extended irreversible thermodynamics revisited (1988-1998), Rep. Prog. Phys. 62 1035-1142
- ↑ Lebon G, Jou D, Casas-Vazquez J (2008), Understanding Non-equilibrium Thermodynamics, Springer, Berlin
- ↑ Jou D, Casas-Vázquez J, Lebon G (2010), Extended Irreversible Thermodynamics, 4th edition,
- ↑ Jou D, Casas-Vazquez J, Criado-Sancho M (2011), Thermodynamics of Fluids under Flow, 2nd edition, Springer, Berlin