
Frequentist probability or frequentism is an interpretation of probability; it defines an event's probability as the limit of its relative frequency in many trials. Probabilities can be found by a repeatable objective process. The continued use of frequentist methods in scientific inference, however, has been called into question.
In statistics, the likelihood principle is the proposition that, given a statistical model, all the evidence in a sample relevant to model parameters is contained in the likelihood function.

Statistical inference is the process of using data analysis to infer properties of an underlying distribution of probability. Inferential statistical analysis infers properties of a population, for example by testing hypotheses and deriving estimates. It is assumed that the observed data set is sampled from a larger population.
A statistical hypothesis test is a method of statistical inference used to decide whether the data at hand sufficiently support a particular hypothesis. More generally, hypothesis testing allows us to make probabilistic statements about population parameters. More informally, hypothesis testing is the processes of making decisions under uncertainty. Typically, hypothesis testing procedures involve a user selected tradeoff between false positives and false negatives.
The likelihood function is the joint probability of observed data viewed as a function of the parameters of a statistical model.
Bayesian inference is a method of statistical inference in which Bayes' theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Fundamentally, Bayesian inference uses prior knowledge, in the form of a prior distribution in order to estimate posterior probabilities. Bayesian inference is an important technique in statistics, and especially in mathematical statistics. Bayesian updating is particularly important in the dynamic analysis of a sequence of data. Bayesian inference has found application in a wide range of activities, including science, engineering, philosophy, medicine, sport, and law. In the philosophy of decision theory, Bayesian inference is closely related to subjective probability, often called "Bayesian probability".
In statistics, interval estimation is the use of sample data to estimate an interval of possible values of a parameter of interest. This is in contrast to point estimation, which gives a single value.
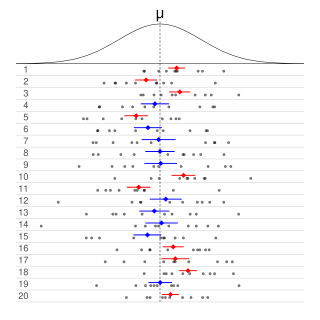
Informally, in frequentist statistics, a confidence interval (CI) is an interval which is expected to typically contain the parameter being estimated. More specifically, given a confidence level , a CI is a random interval which contains the parameter being estimated % of the time. The confidence level, degree of confidence or confidence coefficient represents the long-run proportion of CIs that theoretically contain the true value of the parameter; this is tantamount to the nominal coverage probability. For example, out of all intervals computed at the 95% level, 95% of them should contain the parameter's true value.
In statistical inference, specifically predictive inference, a prediction interval is an estimate of an interval in which a future observation will fall, with a certain probability, given what has already been observed. Prediction intervals are often used in regression analysis.
This glossary of statistics and probability is a list of definitions of terms and concepts used in the mathematical sciences of statistics and probability, their sub-disciplines, and related fields. For additional related terms, see Glossary of mathematics and Glossary of experimental design.
In statistics, the Behrens–Fisher problem, named after Walter-Ulrich Behrens and Ronald Fisher, is the problem of interval estimation and hypothesis testing concerning the difference between the means of two normally distributed populations when the variances of the two populations are not assumed to be equal, based on two independent samples.
In Bayesian statistics, a credible interval is an interval within which an unobserved parameter value falls with a particular probability. It is an interval in the domain of a posterior probability distribution or a predictive distribution. The generalisation to multivariate problems is the credible region.
Statistics, in the modern sense of the word, began evolving in the 18th century in response to the novel needs of industrializing sovereign states.
Statistics models the collection, organization, analysis, interpretation, presentation of data, and is used to solve mathematical problems. Conclusions drawn from statistical analysis typically contain uncertainties, certainties or as they represent the probability of an event occurring. Statistics is fundamental to disciplines of science that involve predicting or classifying events based on a large set of data and is an integral part of fields such as machine learning, bioinformatics, genomics, and economics.
Frequentist inference is a type of statistical inference based in frequentist probability, which treats “probability” in equivalent terms to “frequency” and draws conclusions from sample-data by means of emphasizing the frequency or proportion of findings in the data. Frequentist-inference underlies frequentist statistics, in which the well-established methodologies of statistical hypothesis testing and confidence intervals are founded.
Algorithmic inference gathers new developments in the statistical inference methods made feasible by the powerful computing devices widely available to any data analyst. Cornerstones in this field are computational learning theory, granular computing, bioinformatics, and, long ago, structural probability . The main focus is on the algorithms which compute statistics rooting the study of a random phenomenon, along with the amount of data they must feed on to produce reliable results. This shifts the interest of mathematicians from the study of the distribution laws to the functional properties of the statistics, and the interest of computer scientists from the algorithms for processing data to the information they process.
In statistics, the t-statistic is the ratio of the departure of the estimated value of a parameter from its hypothesized value to its standard error. It is used in hypothesis testing via Student's t-test. The t-statistic is used in a t-test to determine whether to support or reject the null hypothesis. It is very similar to the z-score but with the difference that t-statistic is used when the sample size is small or the population standard deviation is unknown. For example, the t-statistic is used in estimating the population mean from a sampling distribution of sample means if the population standard deviation is unknown. It is also used along with p-value when running hypothesis tests where the p-value tells us what the odds are of the results to have happened.
In statistical inference, the concept of a confidence distribution (CD) has often been loosely referred to as a distribution function on the parameter space that can represent confidence intervals of all levels for a parameter of interest. Historically, it has typically been constructed by inverting the upper limits of lower sided confidence intervals of all levels, and it was also commonly associated with a fiducial interpretation, although it is a purely frequentist concept. A confidence distribution is NOT a probability distribution function of the parameter of interest, but may still be a function useful for making inferences.
In Bayesian inference, the Bernstein–von Mises theorem provides the basis for using Bayesian credible sets for confidence statements in parametric models. It states that under some conditions, a posterior distribution converges in the limit of infinite data to a multivariate normal distribution centered at the maximum likelihood estimator with covariance matrix given by , where is the true population parameter and is the Fisher information matrix at the true population parameter value:
In particle physics, CLs represents a statistical method for setting upper limits on model parameters, a particular form of interval estimation used for parameters that can take only non-negative values. Although CLs are said to refer to Confidence Levels, "The method's name is ... misleading, as the CLs exclusion region is not a confidence interval." It was first introduced by physicists working at the LEP experiment at CERN and has since been used by many high energy physics experiments. It is a frequentist method in the sense that the properties of the limit are defined by means of error probabilities, however it differs from standard confidence intervals in that the stated confidence level of the interval is not equal to its coverage probability. The reason for this deviation is that standard upper limits based on a most powerful test necessarily produce empty intervals with some fixed probability when the parameter value is zero, and this property is considered undesirable by most physicists and statisticians.








