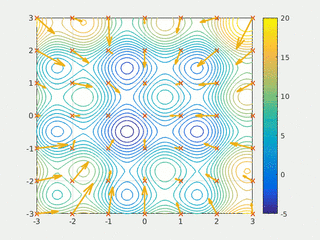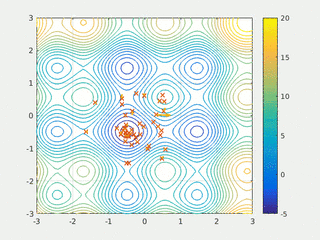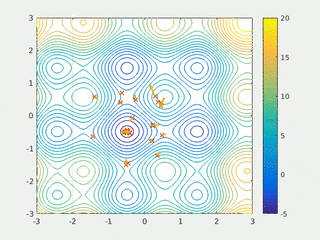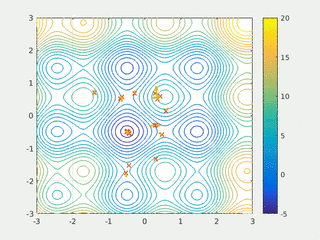
In computational science, particle swarm optimization (PSO) is a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. It solves a problem by having a population of candidate solutions, here dubbed particles, and moving these particles around in the search-space according to simple mathematical formula over the particle's position and velocity. Each particle's movement is influenced by its local best known position, but is also guided toward the best known positions in the search-space, which are updated as better positions are found by other particles. This is expected to move the swarm toward the best solutions.
A fitness function is a particular type of objective function that is used to summarise, as a single figure of merit, how close a given design solution is to achieving the set aims. Fitness functions are used in evolutionary algorithms (EA), such as genetic programming and genetic algorithms to guide simulations towards optimal design solutions.

In computer science and operations research, the ant colony optimization algorithm (ACO) is a probabilistic technique for solving computational problems which can be reduced to finding good paths through graphs. Artificial ants stand for multi-agent methods inspired by the behavior of real ants. The pheromone-based communication of biological ants is often the predominant paradigm used. Combinations of artificial ants and local search algorithms have become a method of choice for numerous optimization tasks involving some sort of graph, e.g., vehicle routing and internet routing.

Stochastic gradient descent is an iterative method for optimizing an objective function with suitable smoothness properties. It can be regarded as a stochastic approximation of gradient descent optimization, since it replaces the actual gradient by an estimate thereof. Especially in high-dimensional optimization problems this reduces the very high computational burden, achieving faster iterations in trade for a lower convergence rate.

In machine learning, backpropagation is a widely used algorithm for training feedforward artificial neural networks. Generalizations of backpropagation exist for other artificial neural networks (ANNs), and for functions generally. These classes of algorithms are all referred to generically as "backpropagation". In fitting a neural network, backpropagation computes the gradient of the loss function with respect to the weights of the network for a single input–output example, and does so efficiently, unlike a naive direct computation of the gradient with respect to each weight individually. This efficiency makes it feasible to use gradient methods for training multilayer networks, updating weights to minimize loss; gradient descent, or variants such as stochastic gradient descent, are commonly used. The backpropagation algorithm works by computing the gradient of the loss function with respect to each weight by the chain rule, computing the gradient one layer at a time, iterating backward from the last layer to avoid redundant calculations of intermediate terms in the chain rule; this is an example of dynamic programming.
Mehrotra's predictor–corrector method in optimization is a specific interior point method for linear programming. It was proposed in 1989 by Sanjay Mehrotra.
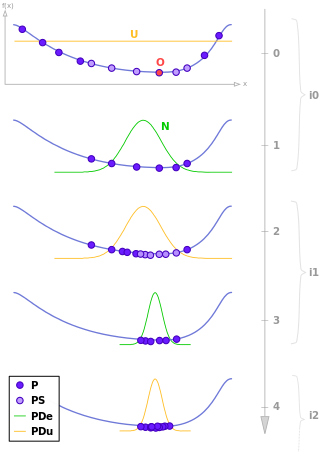
Estimation of distribution algorithms (EDAs), sometimes called probabilistic model-building genetic algorithms (PMBGAs), are stochastic optimization methods that guide the search for the optimum by building and sampling explicit probabilistic models of promising candidate solutions. Optimization is viewed as a series of incremental updates of a probabilistic model, starting with the model encoding an uninformative prior over admissible solutions and ending with the model that generates only the global optima.
Quasi-Newton methods are methods used to either find zeroes or local maxima and minima of functions, as an alternative to Newton's method. They can be used if the Jacobian or Hessian is unavailable or is too expensive to compute at every iteration. The "full" Newton's method requires the Jacobian in order to search for zeros, or the Hessian for finding extrema.
Stochastic approximation methods are a family of iterative methods typically used for root-finding problems or for optimization problems. The recursive update rules of stochastic approximation methods can be used, among other things, for solving linear systems when the collected data is corrupted by noise, or for approximating extreme values of functions which cannot be computed directly, but only estimated via noisy observations.
In numerical optimization, the nonlinear conjugate gradient method generalizes the conjugate gradient method to nonlinear optimization. For a quadratic function
Multi-objective optimization is an area of multiple criteria decision making that is concerned with mathematical optimization problems involving more than one objective function to be optimized simultaneously. Multi-objective optimization has been applied in many fields of science, including engineering, economics and logistics where optimal decisions need to be taken in the presence of trade-offs between two or more conflicting objectives. Minimizing cost while maximizing comfort while buying a car, and maximizing performance whilst minimizing fuel consumption and emission of pollutants of a vehicle are examples of multi-objective optimization problems involving two and three objectives, respectively. In practical problems, there can be more than three objectives.
In operations research, cuckoo search is an optimization algorithm developed by Xin-She Yang and Suash Deb in 2009. It was inspired by the obligate brood parasitism of some cuckoo species by laying their eggs in the nests of host birds of other species. Some host birds can engage direct conflict with the intruding cuckoos. For example, if a host bird discovers the eggs are not their own, it will either throw these alien eggs away or simply abandon its nest and build a new nest elsewhere. Some cuckoo species such as the New World brood-parasitic Tapera have evolved in such a way that female parasitic cuckoos are often very specialized in the mimicry in colors and pattern of the eggs of a few chosen host species. Cuckoo search idealized such breeding behavior, and thus can be applied for various optimization problems. It has been shown that cuckoo search is a special case of the well-known -evolution strategy.
Moving horizon estimation (MHE) is an optimization approach that uses a series of measurements observed over time, containing noise and other inaccuracies, and produces estimates of unknown variables or parameters. Unlike deterministic approaches, MHE requires an iterative approach that relies on linear programming or nonlinear programming solvers to find a solution.

In machine learning, the vanishing gradient problem is encountered when training artificial neural networks with gradient-based learning methods and backpropagation. In such methods, during each iteration of training each of the neural network's weights receives an update proportional to the partial derivative of the error function with respect to the current weight. The problem is that in some cases, the gradient will be vanishingly small, effectively preventing the weight from changing its value. In the worst case, this may completely stop the neural network from further training. As one example of the problem cause, traditional activation functions such as the hyperbolic tangent function have gradients in the range (0,1], and backpropagation computes gradients by the chain rule. This has the effect of multiplying n of these small numbers to compute gradients of the early layers in an n-layer network, meaning that the gradient decreases exponentially with n while the early layers train very slowly.
The multiplicative weights update method is an algorithmic technique most commonly used for decision making and prediction, and also widely deployed in game theory and algorithm design. The simplest use case is the problem of prediction from expert advice, in which a decision maker needs to iteratively decide on an expert whose advice to follow. The method assigns initial weights to the experts, and updates these weights multiplicatively and iteratively according to the feedback of how well an expert performed: reducing it in case of poor performance, and increasing it otherwise. It was discovered repeatedly in very diverse fields such as machine learning, optimization, theoretical computer science, and game theory.
Quantum counting algorithm is a quantum algorithm for efficiently counting the number of solutions for a given search problem. The algorithm is based on the quantum phase estimation algorithm and on Grover's search algorithm.
In mathematics, the spiral optimization (SPO) algorithm is a metaheuristic inspired by spiral phenomena in nature.
A central problem in algorithmic graph theory is the shortest path problem. One of the generalizations of the shortest path problem is known as the single-source-shortest-paths (SSSP) problem, which consists of finding the shortest path between every pair of vertices in a graph. There are classical sequential algorithms which solve this problem, such as Dijkstra's algorithm. In this article, however, we present two parallel algorithms solving this problem.
Powell's dog leg method is an iterative optimisation algorithm for the solution of non-linear least squares problems, introduced in 1970 by Michael J. D. Powell. Similarly to the Levenberg–Marquardt algorithm, it combines the Gauss–Newton algorithm with gradient descent, but it uses an explicit trust region. At each iteration, if the step from the Gauss–Newton algorithm is within the trust region, it is used to update the current solution. If not, the algorithm searches for the minimum of the objective function along the steepest descent direction, known as Cauchy point. If the Cauchy point is outside of the trust region, it is truncated to the boundary of the latter and it is taken as the new solution. If the Cauchy point is inside the trust region, the new solution is taken at the intersection between the trust region boundary and the line joining the Cauchy point and the Gauss-Newton step.




































