
The five room puzzle is a classical, [1] popular puzzle involving a large rectangle divided into five "rooms". The objective of the puzzle is to cross each "wall" of the diagram with a continuous line only once. [2]

The five room puzzle is a classical, [1] popular puzzle involving a large rectangle divided into five "rooms". The objective of the puzzle is to cross each "wall" of the diagram with a continuous line only once. [2]

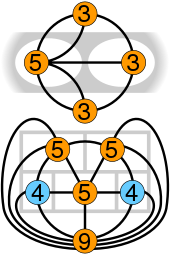
As with the Seven Bridges of Königsberg, the puzzle may be represented in graphical form with each room corresponding to a vertex (including the outside area as a room) and two vertices joined by an edge if the rooms have a common wall. Because there is more than one pair of vertices with an odd number of edges, the resulting multigraph does not contain an Eulerian path nor an Eulerian circuit, which means that this puzzle cannot be solved.
By bending the rules, a related puzzle could be solved. For instance, by permitting passage through more than one wall at a time (that is, through a corner of a room), or by solving the puzzle on a torus (doughnut) instead of a flat plane.
Even without using graph theory, it is not difficult to show that the Five Room Puzzle has no solution. First, the rules must be clarified. The rooms and the solution line must all be drawn on a single side of a normal flat sheet of paper. The solution line must be continuous, but can bend sharply or smoothly in any way and can even cross over itself (but not at a wall, so this is often prohibited). The solution line must cross over each "wall" exactly once, where "cross over" means to pass completely from one to the other of the two rooms that are separated by the "wall", or from a room to the area outside the drawing. This precludes "crossing" two walls at the same time by drawing the solution line through the corner at which they meet. It also precludes "crossing" a wall by drawing the solution line up to a wall, perhaps along it, but then leaving the wall on the same side. There are 16 "walls", seven separating rooms and nine separating the rooms from the area outside the drawing.
The method of proof is proof by contradiction. That is, we proceed as if a solution exists and discover some properties of all solutions. These put us in an impossible situation and thus we have to conclude that we were wrong - there is no solution after all. [3]
Imagine that there is an "observer" in each "room". The observer can see the solution line when it is in his room, but not otherwise. As the solution line is drawn, he will see it enter his room through one wall and leave through another. He may also see that the line starts in his room and/or ends in his room. There is no observer in the area outside the drawing, so there are five observers.
Consider, first, the observers in the lower-left and lower-right rooms. Each of these rooms has four walls. If the solution line starts in one of these rooms, its observer will see the line leave through a wall. Then it will come back into the room through another wall and leave again through a third. Finally, it will come back into the room through the fourth wall and end. If the solution line starts somewhere else, the observer will see the solution line come into and leave his room exactly twice, passing through all four walls in some order. There is no problem with any of this.
Consider, however, the observers in the remaining three rooms. Each of these rooms has five walls. If the solution line starts in one of these rooms, its observer will see the line leave (through one wall), re-enter and leave again (two more walls) and enter and leave a second time (the last two walls). If the solution line starts somewhere else, the observer will see the solution line enter and leave (two walls), enter and leave a second time (two more walls) and finally enter through the fifth wall and end (all five walls have been crossed, so the line cannot get back out of the room again). So, we see that for the rooms with five walls, the solution line must either start inside the room or it must end inside the room. There is no other possibility. In our arguments, we have said nothing about exactly which walls the solution line crosses, the order in which it crosses them or where the line goes when it is outside a particular room. Therefore, these arguments apply to all solutions that obey the rules. Again, for the rooms with five walls, the solution line must either start or end inside the room.
But, we have three rooms with five walls. The solution line has one start and one end, so it can pass through all five walls of two of these rooms. However, having run out of ends, the line can not pass through all of the walls of the third five-walled room. Therefore, the solution line cannot be drawn to obey the rules.
Sprouts is an impartial paper-and-pencil game which can be analyzed for its mathematical properties. It was invented by mathematicians John Horton Conway and Michael S. Paterson at Cambridge University in the early 1960s. The setup is even simpler than the popular Dots and Boxes game, but game-play develops much more artistically and organically.

Life A User's Manual is Georges Perec's most famous novel, published in 1978, first translated into English by David Bellos in 1987. Its title page describes it as "novels", in the plural, the reasons for which become apparent on reading. Some critics have cited the work as an example of postmodern fiction, but Perec preferred to avoid labels and his only long-term affiliation with any movement was with the Oulipo or OUvroir de LIttérature POtentielle.
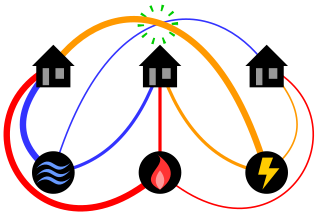
The classical mathematical puzzle known as the three utilities problem or sometimes water, gas and electricity asks for non-crossing connections to be drawn between three houses and three utility companies in the plane. When posing it in the early 20th century, Henry Dudeney wrote that it was already an old problem. It is an impossible puzzle: it is not possible to connect all nine lines without crossing. Versions of the problem on nonplanar surfaces such as a torus or Möbius strip, or that allow connections to pass through other houses or utilities, can be solved.

The Seven Bridges of Königsberg is a historically notable problem in mathematics. Its negative resolution by Leonhard Euler in 1736 laid the foundations of graph theory and prefigured the idea of topology.

In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle that visits each vertex exactly once. A Hamiltonian path that starts and ends at adjacent vertices can be completed by adding one more edge to form a Hamiltonian cycle, and removing any edge from a Hamiltonian cycle produces a Hamiltonian path. Determining whether such paths and cycles exist in graphs are NP-complete.
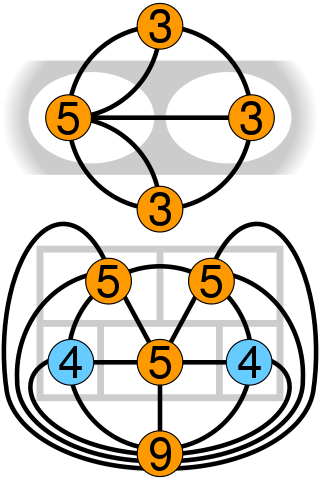
In graph theory, an Eulerian trail is a trail in a finite graph that visits every edge exactly once. Similarly, an Eulerian circuit or Eulerian cycle is an Eulerian trail that starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of Königsberg problem in 1736. The problem can be stated mathematically like this:

Induction puzzles are logic puzzles, which are examples of multi-agent reasoning, where the solution evolves along with the principle of induction.
The Eggerland (エッガーランド) series consists of several puzzle games developed by HAL Laboratory. Its first release was in 1985 for MSX computer systems. Many titles were made in the series and the gameplay is almost exactly the same in every game as well. Only a few changes were made over the years.

Masyu is a type of logic puzzle designed and published by Nikoli. The purpose of its creation was to present a puzzle that uses no numbers or letters and yet retains depth and aesthetics.

Heyawake is a binary-determination logic puzzle published by Nikoli. As of 2013, five books consisting entirely of Heyawake puzzles have been published by Nikoli. It first appeared in Puzzle Communication Nikoli #39.

Slitherlink is a logic puzzle developed by publisher Nikoli.
The crossed ladders problem is a puzzle of unknown origin that has appeared in various publications and regularly reappears in Web pages and Usenet discussions.

Kwirk, known in Japan as Puzzle Boy, is a puzzle video game developed and published by Atlus in Japan on November 24, 1989, for the Game Boy. The game was later published in North America in March 1990 by Acclaim Entertainment.

A maze-solving algorithm is an automated method for solving a maze. The random mouse, wall follower, Pledge, and Trémaux's algorithms are designed to be used inside the maze by a traveler with no prior knowledge of the maze, whereas the dead-end filling and shortest path algorithms are designed to be used by a person or computer program that can see the whole maze at once.

Exit is an American game show on Syfy that premiered on June 4, 2013.
The Challenge: Final Reckoning is the thirty-second season of the MTV reality competition series The Challenge. This season featured alumni from The Real World, Road Rules, The Challenge, Are You the One?, the U.S. version of Big Brother, and the U.K. television shows Ex on the Beach and Geordie Shore, competing along with, for the first time, alumni from Bad Girls Club and Vanderpump Rules who appeared on the U.S. version of Ex on the Beach. The season premiered on July 10, 2018 on MTV.

The first season of The Challenge: All Stars premiered on Paramount+ on April 1, 2021. The season featured twenty-two past cast members of the main series competing for $500,000.
The third season of The Challenge: All Stars premiered on Paramount+ on May 11, 2022. The season features twenty-five past cast members from the main series competing for $500,000.

The Challenge: Ride or Dies is the thirty-eighth season of the MTV reality competition series The Challenge, featuring alumni from The Real World, Road Rules, The Challenge, Are You the One?, Big Brother, Ex on the Beach, Survivor, Love Island, Ultimate Beastmaster, Prince Charming, The Mole Germany, Beauty & The Nerd and Exatlon (U.S.) competing for a share at a $1 million prize. The season premiered on October 12, 2022, preceded by a launch special titled "Ready to Ride" which aired on October 10, 2022.