Forbidden graph characterization

Last updated

In graph theory, a branch of mathematics, many important families of graphs can be described by a finite set of individual graphs that do not belong to the family and further exclude all graphs from the family which contain any of these forbidden graphs as (induced) subgraph or minor.

Contents

A prototypical example of this phenomenon is Kuratowski's theorem, which states that a graph is planar (can be drawn without crossings in the plane) if and only if it does not contain either of two forbidden graphs, the complete graph K5 and the complete bipartite graph K3,3. For Kuratowski's theorem, the notion of containment is that of graph homeomorphism, in which a subdivision of one graph appears as a subgraph of the other. Thus, every graph either has a planar drawing (in which case it belongs to the family of planar graphs) or it has a subdivision of at least one of these two graphs as a subgraph (in which case it does not belong to the planar graphs).

Definition

More generally, a forbidden graph characterization is a method of specifying a family of graph, or hypergraph, structures, by specifying substructures that are forbidden to exist within any graph in the family. Different families vary in the nature of what is forbidden. In general, a structure G is a member of a family if and only if a forbidden substructure is not contained in G. The forbidden substructure might be one of:

The set of structures that are forbidden from belonging to a given graph family can also be called an obstruction set for that family.

Forbidden graph characterizations may be used in algorithms for testing whether a graph belongs to a given family. In many cases, it is possible to test in polynomial time whether a given graph contains any of the members of the obstruction set, and therefore whether it belongs to the family defined by that obstruction set.

In order for a family to have a forbidden graph characterization, with a particular type of substructure, the family must be closed under substructures. That is, every substructure (of a given type) of a graph in the family must be another graph in the family. Equivalently, if a graph is not part of the family, all larger graphs containing it as a substructure must also be excluded from the family. When this is true, there always exists an obstruction set (the set of graphs that are not in the family but whose smaller substructures all belong to the family). However, for some notions of what a substructure is, this obstruction set could be infinite. The Robertson–Seymour theorem proves that, for the particular case of graph minors, a family that is closed under minors always has a finite obstruction set.

List of forbidden characterizations for graphs and hypergraphs

FamilyObstructionsRelationReference
Forests Loops, pairs of parallel edges, and cycles of all lengthsSubgraphDefinition
A loop (for multigraphs) or triangle K3 (for simple graphs)Graph minorDefinition
Linear forests [A loop / triangle K3 (see above)] and star K1,3Graph minorDefinition
Claw-free graphs Star K1,3Induced subgraphDefinition
Comparability graphs Induced subgraph
Triangle-free graphs Triangle K3Induced subgraphDefinition
Planar graphs K5 and K3,3Homeomorphic subgraph Kuratowski's theorem
K5 and K3,3Graph minor Wagner's theorem
Outerplanar graphs K4 and K2,3Graph minor Diestel (2000), [1] p. 107
Outer 1-planar graphs Six forbidden minorsGraph minor Auer et al. (2013) [2]
Graphs of fixed genus A finite obstruction setGraph minor Diestel (2000), [1] p. 275
Apex graphs A finite obstruction setGraph minor [3]
Linklessly embeddable graphs The Petersen family Graph minor [4]
Bipartite graphs Odd cyclesSubgraph [5]
Chordal graphs Cycles of length 4 or moreInduced subgraph [6]
Perfect graphs Cycles of odd length 5 or more or their complements Induced subgraph [7]
Line graph of graphs 9 forbidden subgraphs Induced subgraph [8]
Graph unions of cactus graphs The four-vertex diamond graph formed by removing an edge from the complete graph K4Graph minor [9]
Ladder graphs K2,3 and its dual graph Homeomorphic subgraph [10]
Split graphs Induced subgraph [11]
2-connected series–parallel (treewidth ≤ 2, branchwidth  ≤ 2)K4Graph minor Diestel (2000), [1] p. 327
Treewidth ≤ 3K5, octahedron, pentagonal prism, Wagner graph Graph minor [12]
Branchwidth ≤ 3K5, octahedron, cube, Wagner graph Graph minor [13]
Complement-reducible graphs (cographs) 4-vertex path P4Induced subgraph [14]
Trivially perfect graphs 4-vertex path P4 and 4-vertex cycle C4Induced subgraph [15]
Threshold graphs 4-vertex path P4, 4-vertex cycle C4, and complement of C4Induced subgraph [15]
Line graph of 3-uniform linear hypergraphs A finite list of forbidden induced subgraphs with minimum degree at least 19Induced subgraph [16]
Line graph of k-uniform linear hypergraphs, k > 3 A finite list of forbidden induced subgraphs with minimum edge degree at least 2k2 − 3k + 1Induced subgraph [17] [18]
Graphs ΔY-reducible to a single vertexA finite list of at least 68 billion distinct (1,2,3)-clique sumsGraph minor [19]
Graphs of spectral radius at most A finite obstruction set exists if and only if and for any , where is the largest root of .Subgraph / induced subgraph [20]
Cluster graphs three-vertex path graphInduced subgraph
General theorems
A family defined by an induced-hereditary property A, possibly non-finite, obstruction setInduced subgraph
A family defined by a minor-hereditary property A finite obstruction setGraph minor Robertson–Seymour theorem

See also

Related Research Articles

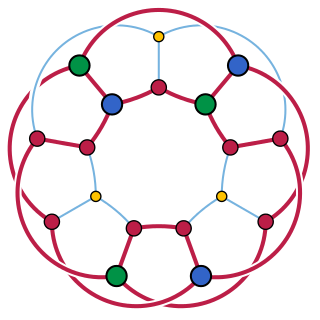
<span class="mw-page-title-main">Kuratowski's theorem</span> On forbidden subgraphs in planar graphs

In graph theory, Kuratowski's theorem is a mathematical forbidden graph characterization of planar graphs, named after Kazimierz Kuratowski. It states that a finite graph is planar if and only if it does not contain a subgraph that is a subdivision of or of .

In graph theory, the Robertson–Seymour theorem states that the undirected graphs, partially ordered by the graph minor relationship, form a well-quasi-ordering. Equivalently, every family of graphs that is closed under minors can be defined by a finite set of forbidden minors, in the same way that Wagner's theorem characterizes the planar graphs as being the graphs that do not have the complete graph K5 or the complete bipartite graph K3,3 as minors.

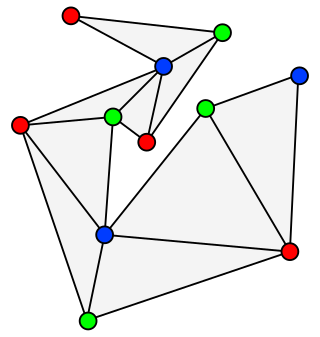
<span class="mw-page-title-main">Outerplanar graph</span> Non-crossing graph with vertices on outer face

In graph theory, an outerplanar graph is a graph that has a planar drawing for which all vertices belong to the outer face of the drawing.

In graph theory, an undirected graph H is called a minor of the graph G if H can be formed from G by deleting edges, vertices and by contracting edges.

<span class="mw-page-title-main">Clique (graph theory)</span> Subset of the vertices of a node-link graph that are all adjacent to each other

In the mathematical area of graph theory, a clique is a subset of vertices of an undirected graph such that every two distinct vertices in the clique are adjacent. That is, a clique of a graph is an induced subgraph of that is complete. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs. Cliques have also been studied in computer science: the task of finding whether there is a clique of a given size in a graph is NP-complete, but despite this hardness result, many algorithms for finding cliques have been studied.

In mathematics, a universal graph is an infinite graph that contains every finite graph as an induced subgraph. A universal graph of this type was first constructed by Richard Rado and is now called the Rado graph or random graph. More recent work has focused on universal graphs for a graph family F: that is, an infinite graph belonging to F that contains all finite graphs in F. For instance, the Henson graphs are universal in this sense for the i-clique-free graphs.

In mathematics, a dense graph is a graph in which the number of edges is close to the maximal number of edges. The opposite, a graph with only a few edges, is a sparse graph. The distinction of what constitutes a dense or sparse graph is ill-defined, and is often represented by 'roughly equal to' statements. Due to this, the way that density is defined often depends on the context of the problem.

<span class="mw-page-title-main">Wagner's theorem</span> On forbidden minors in planar graphs

In graph theory, Wagner's theorem is a mathematical forbidden graph characterization of planar graphs, named after Klaus Wagner, stating that a finite graph is planar if and only if its minors include neither K5 nor K3,3. This was one of the earliest results in the theory of graph minors and can be seen as a forerunner of the Robertson–Seymour theorem.

In graph theory, the treewidth of an undirected graph is an integer number which specifies, informally, how far the graph is from being a tree. The smallest treewidth is 1; the graphs with treewidth 1 are exactly the trees and the forests. The graphs with treewidth at most 2 are the series–parallel graphs. The maximal graphs with treewidth exactly k are called k-trees, and the graphs with treewidth at most k are called partial k-trees. Many other well-studied graph families also have bounded treewidth.

In graph theory, a path decomposition of a graph G is, informally, a representation of G as a "thickened" path graph, and the pathwidth of G is a number that measures how much the path was thickened to form G. More formally, a path-decomposition is a sequence of subsets of vertices of G such that the endpoints of each edge appear in one of the subsets and such that each vertex appears in a contiguous subsequence of the subsets, and the pathwidth is one less than the size of the largest set in such a decomposition. Pathwidth is also known as interval thickness, vertex separation number, or node searching number.

<span class="mw-page-title-main">Grötzsch graph</span> Triangle-free graph requiring four colors

In the mathematical field of graph theory, the Grötzsch graph is a triangle-free graph with 11 vertices, 20 edges, chromatic number 4, and crossing number 5. It is named after German mathematician Herbert Grötzsch, who used it as an example in connection with his 1959 theorem that planar triangle-free graphs are 3-colorable.

In graph theory, the planarity testing problem is the algorithmic problem of testing whether a given graph is a planar graph (that is, whether it can be drawn in the plane without edge intersections). This is a well-studied problem in computer science for which many practical algorithms have emerged, many taking advantage of novel data structures. Most of these methods operate in O(n) time (linear time), where n is the number of edges (or vertices) in the graph, which is asymptotically optimal. Rather than just being a single Boolean value, the output of a planarity testing algorithm may be a planar graph embedding, if the graph is planar, or an obstacle to planarity such as a Kuratowski subgraph if it is not.

<span class="mw-page-title-main">Branch-decomposition</span> Hierarchical clustering of graph edges

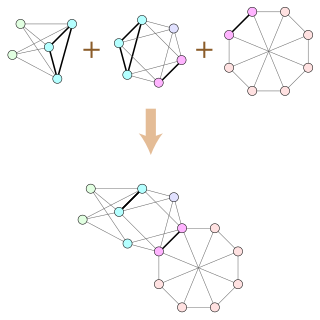
In graph theory, a branch-decomposition of an undirected graph G is a hierarchical clustering of the edges of G, represented by an unrooted binary tree T with the edges of G as its leaves. Removing any edge from T partitions the edges of G into two subgraphs, and the width of the decomposition is the maximum number of shared vertices of any pair of subgraphs formed in this way. The branchwidth of G is the minimum width of any branch-decomposition of G.

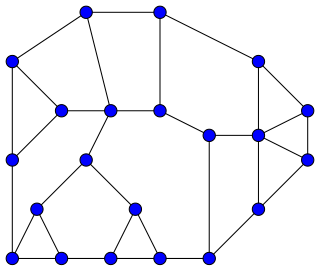
<span class="mw-page-title-main">Halin graph</span> Mathematical tree with cycle through leaves

In graph theory, a Halin graph is a type of planar graph, constructed by connecting the leaves of a tree into a cycle. The tree must have at least four vertices, none of which has exactly two neighbors; it should be drawn in the plane so none of its edges cross, and the cycle connects the leaves in their clockwise ordering in this embedding. Thus, the cycle forms the outer face of the Halin graph, with the tree inside it.

In graph theory, a Trémaux tree of an undirected graph is a type of spanning tree, generalizing depth-first search trees. They are defined by the property that every edge of connects an ancestor–descendant pair in the tree. Trémaux trees are named after Charles Pierre Trémaux, a 19th-century French author who used a form of depth-first search as a strategy for solving mazes. They have also been called normal spanning trees, especially in the context of infinite graphs.

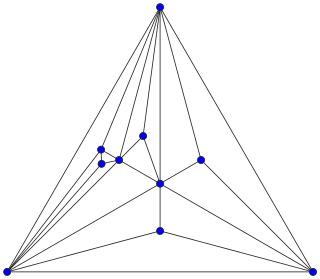
<span class="mw-page-title-main">Apollonian network</span> Graph formed by subdivision of triangles

In combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable planar graphs, and the graphs of stacked polytopes. They are named after Apollonius of Perga, who studied a related circle-packing construction.

<span class="mw-page-title-main">1-planar graph</span>

In topological graph theory, a 1-planar graph is a graph that can be drawn in the Euclidean plane in such a way that each edge has at most one crossing point, where it crosses a single additional edge. If a 1-planar graph, one of the most natural generalizations of planar graphs, is drawn that way, the drawing is called a 1-plane graph or 1-planar embedding of the graph.

<span class="mw-page-title-main">Planar cover</span>

In graph theory, a planar cover of a finite graph G is a finite covering graph of G that is itself a planar graph. Every graph that can be embedded into the projective plane has a planar cover; an unsolved conjecture of Seiya Negami states that these are the only graphs with planar covers.

In graph theory and graph drawing, a subhamiltonian graph is a subgraph of a planar Hamiltonian graph.

In graph theory, a family of graphs is said to have bounded expansion if all of its shallow minors are sparse graphs. Many natural families of sparse graphs have bounded expansion. A closely related but stronger property, polynomial expansion, is equivalent to the existence of separator theorems for these families. Families with these properties have efficient algorithms for problems including the subgraph isomorphism problem and model checking for the first order theory of graphs.

References

  1. 1 2 3 Diestel, Reinhard (2000), Graph Theory, Graduate Texts in Mathematics, vol. 173, Springer-Verlag, ISBN   0-387-98976-5 .
  2. ↑ Auer, Christopher; Bachmaier, Christian; Brandenburg, Franz J.; Gleißner, Andreas; Hanauer, Kathrin; Neuwirth, Daniel; Reislhuber, Josef (2013), "Recognizing outer 1-planar graphs in linear time", in Wismath, Stephen; Wolff, Alexander (eds.), 21st International Symposium, GD 2013, Bordeaux, France, September 23-25, 2013, Revised Selected Papers, Lecture Notes in Computer Science, vol. 8242, pp. 107–118, doi: 10.1007/978-3-319-03841-4_10 .
  3. ↑ Gupta, A.; Impagliazzo, R. (1991), "Computing planar intertwines", Proc. 32nd IEEE Symposium on Foundations of Computer Science (FOCS '91) , IEEE Computer Society, pp. 802–811, doi:10.1109/SFCS.1991.185452, S2CID   209133 .
  4. ↑ Robertson, Neil; Seymour, P. D.; Thomas, Robin (1993), "Linkless embeddings of graphs in 3-space", Bulletin of the American Mathematical Society, 28 (1): 84–89, arXiv: math/9301216 , doi:10.1090/S0273-0979-1993-00335-5, MR   1164063, S2CID   1110662 .
  5. ↑ Béla Bollobás (1998) "Modern Graph Theory", Springer, ISBN   0-387-98488-7 p. 9
  6. ↑ Kashiwabara, Toshinobu (1981), "Algorithms for some intersection graphs", in Saito, Nobuji; Nishizeki, Takao (eds.), Graph Theory and Algorithms, 17th Symposium of Research Institute of Electric Communication, Tohoku University, Sendai, Japan, October 24-25, 1980, Proceedings, Lecture Notes in Computer Science, vol. 108, Springer-Verlag, pp. 171–181, doi: 10.1007/3-540-10704-5_15 .
  7. ↑ Chudnovsky, Maria; Robertson, Neil; Seymour, Paul; Thomas, Robin (2006), "The strong perfect graph theorem" (PDF), Annals of Mathematics , 164 (1): 51–229, arXiv: math/0212070v1 , doi:10.4007/annals.2006.164.51, S2CID   119151552 .
  8. ↑ Beineke, L. W. (1968), "Derived graphs of digraphs", in Sachs, H.; Voss, H.-J.; Walter, H.-J. (eds.), Beiträge zur Graphentheorie, Leipzig: Teubner, pp. 17–33.
  9. ↑ El-Mallah, Ehab; Colbourn, Charles J. (1988), "The complexity of some edge deletion problems", IEEE Transactions on Circuits and Systems, 35 (3): 354–362, doi:10.1109/31.1748 .
  10. ↑ Takamizawa, K.; Nishizeki, Takao; Saito, Nobuji (1981), "Combinatorial problems on series–parallel graphs", Discrete Applied Mathematics, 3 (1): 75–76, doi: 10.1016/0166-218X(81)90031-7 .
  11. ↑ Földes, Stéphane; Hammer, Peter Ladislaw (1977a), "Split graphs", Proceedings of the Eighth Southeastern Conference on Combinatorics, Graph Theory and Computing (Louisiana State Univ., Baton Rouge, La., 1977), Congressus Numerantium, vol. XIX, Winnipeg: Utilitas Math., pp. 311–315, MR   0505860
  12. ↑ Bodlaender, Hans L. (1998), "A partial k-arboretum of graphs with bounded treewidth", Theoretical Computer Science, 209 (1–2): 1–45, doi:10.1016/S0304-3975(97)00228-4, hdl: 1874/18312 .
  13. ↑ Bodlaender, Hans L.; Thilikos, Dimitrios M. (1999), "Graphs with branchwidth at most three", Journal of Algorithms, 32 (2): 167–194, doi:10.1006/jagm.1999.1011, hdl: 1874/2734 .
  14. ↑ Seinsche, D. (1974), "On a property of the class of n-colorable graphs", Journal of Combinatorial Theory , Series B, 16 (2): 191–193, doi: 10.1016/0095-8956(74)90063-X , MR   0337679
  15. 1 2 Golumbic, Martin Charles (1978), "Trivially perfect graphs", Discrete Mathematics , 24 (1): 105–107, doi: 10.1016/0012-365X(78)90178-4 .
  16. ↑ Metelsky, Yury; Tyshkevich, Regina (1997), "On line graphs of linear 3-uniform hypergraphs", Journal of Graph Theory , 25 (4): 243–251, doi:10.1002/(SICI)1097-0118(199708)25:4<243::AID-JGT1>3.0.CO;2-K, MR   1459889
  17. ↑ Jacobson, M. S.; Kézdy, Andre E.; Lehel, Jeno (1997), "Recognizing intersection graphs of linear uniform hypergraphs", Graphs and Combinatorics , 13 (4): 359–367, doi:10.1007/BF03353014, MR   1485929, S2CID   9173731
  18. ↑ Naik, Ranjan N.; Rao, S. B.; Shrikhande, S. S.; Singhi, N. M. (1982), "Intersection graphs of k-uniform hypergraphs", European Journal of Combinatorics , 3: 159–172, doi: 10.1016/s0195-6698(82)80029-2 , MR   0670849
  19. ↑ Yu, Yanming (2006), "More forbidden minors for wye-delta-wye reducibility", The Electronic Journal of Combinatorics, 13, doi: 10.37236/1033 Website
  20. ↑ Jiang, Zilin; Polyanskii, Alexandr (2020-03-01). "Forbidden Subgraphs for Graphs of Bounded Spectral Radius, with Applications to Equiangular Lines". Israel Journal of Mathematics . 236 (1): 393–421. arXiv: 1708.02317 . doi:10.1007/s11856-020-1983-2. ISSN   1565-8511.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.