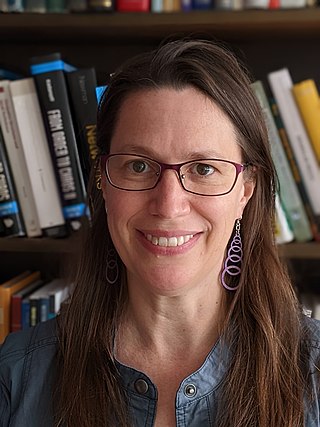Quantum gravity (QG) is a field of theoretical physics that seeks to describe gravity according to the principles of quantum mechanics. It deals with environments in which neither gravitational nor quantum effects can be ignored, such as in the vicinity of black holes or similar compact astrophysical objects, such as neutron stars.

A granular material is a conglomeration of discrete solid, macroscopic particles characterized by a loss of energy whenever the particles interact. The constituents that compose granular material are large enough such that they are not subject to thermal motion fluctuations. Thus, the lower size limit for grains in granular material is about 1 μm. On the upper size limit, the physics of granular materials may be applied to ice floes where the individual grains are icebergs and to asteroid belts of the Solar System with individual grains being asteroids.

Granular convection is a phenomenon where granular material subjected to shaking or vibration will exhibit circulation patterns similar to types of fluid convection. It is sometimes called the Brazil nut effect, when the largest of irregularly shaped particles end up on the surface of a granular material containing a mixture of variously sized objects. This name derives from the example of a typical container of mixed nuts, in which the largest will be Brazil nuts. The phenomenon is also known as the muesli effect since it is seen in packets of breakfast cereal containing particles of different sizes but similar density, such as muesli mix.
Strongly interacting massive particles (SIMPs) are hypothetical particles that interact strongly between themselves and weakly with ordinary matter, but could form the inferred dark matter despite this.
In physics, an oscillon is a soliton-like phenomenon that occurs in granular and other dissipative media. Oscillons in granular media result from vertically vibrating a plate with a layer of uniform particles placed freely on top. When the sinusoidal vibrations are of the correct amplitude and frequency and the layer of sufficient thickness, a localized wave, referred to as an oscillon, can be formed by locally disturbing the particles. This meta-stable state will remain for a long time in the absence of further perturbation. An oscillon changes form with each collision of the grain layer and the plate, switching between a peak that projects above the grain layer to a crater like depression with a small rim. This self-sustaining state was named by analogy with the soliton, which is a localized wave that maintains its integrity as it moves. Whereas solitons occur as travelling waves in a fluid or as electromagnetic waves in a waveguide, oscillons may be stationary.

In physics, topological order is a kind of order in the zero-temperature phase of matter. Macroscopically, topological order is defined and described by robust ground state degeneracy and quantized non-Abelian geometric phases of degenerate ground states. Microscopically, topological orders correspond to patterns of long-range quantum entanglement. States with different topological orders cannot change into each other without a phase transition.
The classical-map hypernetted-chain method is a method used in many-body theoretical physics for interacting uniform electron liquids in two and three dimensions, and for non-ideal plasmas. The method extends the famous hypernetted-chain method (HNC) introduced by J. M. J van Leeuwen et al. to quantum fluids as well. The classical HNC, together with the Percus–Yevick approximation, are the two pillars which bear the brunt of most calculations in the theory of interacting classical fluids. Also, HNC and PY have become important in providing basic reference schemes in the theory of fluids, and hence they are of great importance to the physics of many-particle systems.
Washboarding or corrugation is the formation of periodic, transverse ripples in the surface of gravel and dirt roads. Washboarding occurs in dry, granular road material with repeated traffic, traveling at speeds above 8.0 kilometres per hour (5 mph). Washboarding creates an uncomfortable ride for the occupants of traversing vehicles and hazardous driving conditions for vehicles that travel too fast to maintain traction and control.

Alexander Balankin is a Mexican scientist of Russian origin whose work in the field of fractal mechanics and its engineering applications won him the UNESCO Science Prize in 2005.
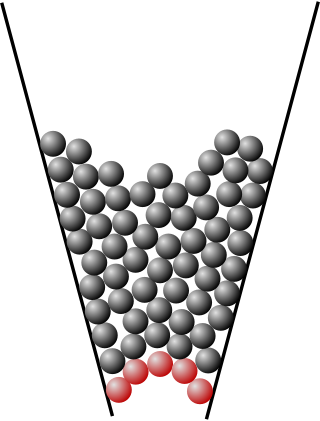
Jamming is the physical process by which the viscosity of some mesoscopic materials, such as granular materials, glasses, foams, polymers, emulsions, and other complex fluids, increases with increasing particle density. The jamming transition has been proposed as a new type of phase transition, with similarities to a glass transition but very different from the formation of crystalline solids.
The muffin-tin approximation is a shape approximation of the potential well in a crystal lattice. It is most commonly employed in quantum mechanical simulations of the electronic band structure in solids. The approximation was proposed by John C. Slater. Augmented plane wave method (APW) is a method which uses muffin-tin approximation. It is a method to approximate the energy states of an electron in a crystal lattice. The basic approximation lies in the potential in which the potential is assumed to be spherically symmetric in the muffin-tin region and constant in the interstitial region. Wave functions are constructed by matching solutions of the Schrödinger equation within each sphere with plane-wave solutions in the interstitial region, and linear combinations of these wave functions are then determined by the variational method. Many modern electronic structure methods employ the approximation. Among them APW method, the linear muffin-tin orbital method (LMTO) and various Green's function methods. One application is found in the variational theory developed by Jan Korringa (1947) and by Walter Kohn and N. Rostoker (1954) referred to as the KKR method. This method has been adapted to treat random materials as well, where it is called the KKR coherent potential approximation.

A colloidal crystal is an ordered array of colloidal particles and fine grained materials analogous to a standard crystal whose repeating subunits are atoms or molecules. A natural example of this phenomenon can be found in the gem opal, where spheres of silica assume a close-packed locally periodic structure under moderate compression. Bulk properties of a colloidal crystal depend on composition, particle size, packing arrangement, and degree of regularity. Applications include photonics, materials processing, and the study of self-assembly and phase transitions.

Lubachevsky-Stillinger (compression) algorithm is a numerical procedure suggested by F. H. Stillinger and B.D. Lubachevsky that simulates or imitates a physical process of compressing an assembly of hard particles. As the LSA may need thousands of arithmetic operations even for a few particles, it is usually carried out on a computer.
Peter Grassberger is a professor (where?) who worked in statistical and particle physics. He made contributions to chaos theory, where he introduced the idea of correlation dimension, a means of measuring a type of fractal dimension of the strange attractor.
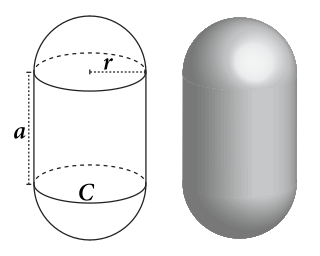
A capsule, or stadium of revolution, is a basic three-dimensional geometric shape consisting of a cylinder with hemispherical ends. Another name for this shape is spherocylinder.
Hyperuniform materials are characterized by an anomalous suppression of density fluctuations at large scales. More precisely, the vanishing of density fluctuations in the long-wave length limit distinguishes hyperuniform systems from typical gases, liquids, or amorphous solids. Examples of hyperuniformity include all perfect crystals, perfect quasicrystals, and exotic amorphous states of matter.
Surajit Sen is a physicist who works on theoretical and computational problems in non-equilibrium statistical physics and in nonlinear dynamics of many body systems. He holds a Ph.D in physics from The University of Georgia (1990) where he studied with M. Howard Lee. He is also interested in applying physics to study problems of relevance in a societal context. He is a professor of physics at the State University of New York, Buffalo.
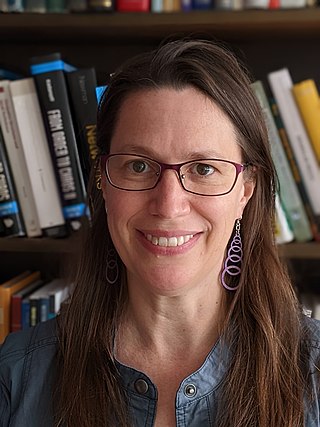
Karen E. Daniels is an American physicist who is a Professor of Physics at North Carolina State University. Her research considers the deformation and failure of materials. She is a Fellow of the American Physical Society, and serves on their Committee on the Status of Women in Physics. She is also a Fellow of the American Association for the Advancement of Science.
Douglas J. Durian is Professor of Physics and Astronomy at the University of Pennsylvania. He is known for his research contributions to the field of experimental soft matter, particularly in the areas of foams and granular flows. He has held multiple visiting professorships and leaderships positions in the soft matter physics community. He is a Fellow of the American Physical Society.
Dov I. Levine is an American-Israeli physicist, known for his research on quasicrystals, soft condensed matter physics, and statistical mechanics out of equilibrium.