Fragment molecular orbital

Last updated

The fragment molecular orbital method (FMO) is a computational method that can be used to calculate very large molecular systems with thousands of atoms using ab initio quantum-chemical wave functions.

Contents

An alpha-helix fragmented for FMO using Facio. Ahelix-FMO-Facio.jpg
An alpha-helix fragmented for FMO using Facio.

The fragment molecular orbital method (FMO) was developed by Kazuo Kitaura and coworkers in 1999. [1] FMO is deeply interconnected with the energy decomposition analysis (EDA) by Kazuo Kitaura and Keiji Morokuma, developed in 1976. The main use of FMO is to compute very large molecular systems by dividing them into fragments and performing ab initio or density functional quantum-mechanical calculations of fragments and their dimers, whereby the Coulomb field from the whole system is included. The latter feature allows fragment calculations without using caps.

The mutually consistent field (MCF) method [2] had introduced the idea of self-consistent fragment calculations in their embedding potential, which was later used with some modifications in various methods including FMO. There had been other methods related to FMO including the incremental correlation method by H. Stoll (1992). [3]

Later, other methods closely related to FMO were proposed including the kernel energy method of L. Huang [4] and the electrostatically embedded many-body expansion by E. Dahlke, [5] S. Hirata [6] and later M. Kamiya [7] suggested approaches also very closely related to FMO. Effective fragment molecular orbital (EFMO) method combines some features of the effective fragment potentials (EFP) and FMO. A detailed perspective on the fragment-based method development can be found in a review. [8]

Introduction to FMO

In addition to the calculation of the total properties, such as the energy, energy gradient, dipole moment etc., an interaction energy is obtained for each pair of fragments. This pair interaction energy can be further decomposed into electrostatic, exchange, charge transfer and dispersion contributions. This analysis is known as the pair interaction energy decomposition analysis (PIEDA) and it can be thought of as FMO-based EDA. Alternatively, configuration analysis for fragment interaction (CAFI) and fragment interaction analysis based on local MP2 (FILM) were suggested within the FMO framework.

In FMO, various wave functions can be used for ab initio calculations of fragments and their dimers, such as Hartree–Fock, Density functional theory (DFT), Multi-configurational self-consistent field (MCSCF), time-dependent DFT (TDDFT), configuration interaction (CI), second order Møller–Plesset perturbation theory (MP2), coupled cluster (CC), and density functional tight binding (DFTB). Excited states can be computed with Configuration interaction (CI), Time-dependent density functional theory (TDDFT), time-dependent DFTB (TD-DFTB), equation-of-motion coupled-cluster (EOM-CC), and GW approximation. The solvent effects can be treated with the Polarizable continuum model (PCM). The FMO code is very efficiently parallelized utilising the generalized distributed data interface (GDDI) and hundreds of CPUs can be used with nearly perfect scaling.

In the FMO book published in 2009, [9] one can find 10 illustrated chapters written by the experts in the FMO development and applications, as well as a CDROM with annotated samples of input and output files, Facio modelling software and video tutorials (AppliGuide movies, showing mouse clicks) for treating difficult PDB files with Facio. In addition to this book, there are several chapters published in other books. [10] [11] [12] [13]

In 2013–2014, a Japanese journal, CICSJ Bulletin, published a series of FMO papers in Japanese (about 100 pages in total), which give a representative summary of the recent FMO development and applications done in Japan, including papers on the GAMESS/FMO interface in Facio and developing an OpenMP version of GAMESS/FMO on the K computer. [14] Later, FMO was ported on the Fugaku [15] and Summit supercomputers. [16]

There are several reviews of FMO published in 2007, [17] 2012, [18] 2014, [19] 2017, [20] and 2022. [21] Two new FMO books were published in 2021 [22] and 2023. [23]

The largest systems computed with FMO using DFTB are (a) a slab of fullerite surface containing 1,030,440 atoms, whose geometry was fully optimized and (b) a 10.7 μm white graphene nano material containing 1,180,800 atoms, for which Molecular dynamics simulations were performed.

To facilitate applications of FMO to drug discovery, FMO consortium was established. [24]

Applications of FMO

There are two main application fields of FMO: biochemistry and molecular dynamics of chemical reactions in solution. In addition, there is an emerging field of inorganic applications.

In 2005, an application of FMO to the calculation of the ground electronic state of photosynthetic protein with more than 20,000 atoms was distinguished with the best technical paper award at Supercomputing 2005. A number of applications of FMO to biochemical problems has been published, for instance, to Drug design, quantitative structure-activity relationship (QSAR) as well as the studies of excited states and chemical reactions of biological systems. The adaptive frozen orbital (AFO) treatment of the detached bonds was developed for FMO, making it possible to study solids, surfaces and nano systems, such as silicon nanowrires. FMO-TDDFT was applied to the excited states of molecular crystals (quinacridone).

Among inorganic systems, silica-related materials (zeolites, mesoporous nanoparticles and silica surfaces) were studied with FMO, as well as ionic liquids and boron nitride ribbons. There are other applications of FMO. [25]

Software for FMO

The FMO method is implemented in GAMESS (US), ABINIT-MP, [26] PAICS, [27] and OpenFMO [28] software packages, distributed free of charge.

Fu, [29] is a general open-source GUI that can generate input files for FMO. Another graphical user interface Facio [30] developed by M. Suenaga has a very convenient specialised support of FMO (in addition to other features), with which an automatic fragmentation of molecular clusters, proteins, nucleotides, saccharides and any combination thereof (e.g., DNA and protein complexes in explicit solvent) can be done in a few minutes, and a manual fragmentation of solids and surfaces can be accomplished by clicking the bonds to be detached. Facio can also visualise results of FMO calculations, such as the pair interactions.

FMO implementation in GAMESS

(E - energy, G - gradient, H - Hessian; bold - can be used with PCM)

RHF ROHF UHF GVB MCSCF
PlainEGHEGHEGH-EG
MP2EGEGE--
CCEE---
CIE----
DFTEGH-EGH--
TD-DFTEG-E--
EOM-CCE----
DFTB EGH----

See also

Related Research Articles

<span class="mw-page-title-main">Computational chemistry</span> Branch of chemistry

Computational chemistry is a branch of chemistry that uses computer simulations to assist in solving chemical problems. It uses methods of theoretical chemistry incorporated into computer programs to calculate the structures and properties of molecules, groups of molecules, and solids. The importance of this subject stems from the fact that, with the exception of some relatively recent findings related to the hydrogen molecular ion, achieving an accurate quantum mechanical depiction of chemical systems analytically, or in a closed form, is not feasible. The complexity inherent in the many-body problem exacerbates the challenge of providing detailed descriptions of quantum mechanical systems. While computational results normally complement information obtained by chemical experiments, it can occasionally predict unobserved chemical phenomena.

<span class="mw-page-title-main">Molecular dynamics</span> Computer simulations to discover and understand chemical properties

Molecular dynamics (MD) is a computer simulation method for analyzing the physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a fixed period of time, giving a view of the dynamic "evolution" of the system. In the most common version, the trajectories of atoms and molecules are determined by numerically solving Newton's equations of motion for a system of interacting particles, where forces between the particles and their potential energies are often calculated using interatomic potentials or molecular mechanical force fields. The method is applied mostly in chemical physics, materials science, and biophysics.

<span class="mw-page-title-main">Excited state</span> Quantum states with more energy than the lowest possible amount

In quantum mechanics, an excited state of a system is any quantum state of the system that has a higher energy than the ground state. Excitation refers to an increase in energy level above a chosen starting point, usually the ground state, but sometimes an already excited state. The temperature of a group of particles is indicative of the level of excitation.

<span class="mw-page-title-main">MOLPRO</span> Ab initio quantum chemistry software package

MOLPRO is a software package used for accurate ab initio quantum chemistry calculations. It is developed by Peter Knowles at Cardiff University and Hans-Joachim Werner at Universität Stuttgart in collaboration with other authors.

Q-Chem is a general-purpose electronic structure package featuring a variety of established and new methods implemented using innovative algorithms that enable fast calculations of large systems on various computer architectures, from laptops and regular lab workstations to midsize clusters, HPCC, and cloud computing using density functional and wave-function based approaches. It offers an integrated graphical interface and input generator; a large selection of functionals and correlation methods, including methods for electronically excited states and open-shell systems; solvation models; and wave-function analysis tools. In addition to serving the computational chemistry community, Q-Chem also provides a versatile code development platform.

Vibronic coupling in a molecule involves the interaction between electronic and nuclear vibrational motion. The term "vibronic" originates from the combination of the terms "vibrational" and "electronic", denoting the idea that in a molecule, vibrational and electronic interactions are interrelated and influence each other. The magnitude of vibronic coupling reflects the degree of such interrelation.

Koopmans' theorem states that in closed-shell Hartree–Fock theory (HF), the first ionization energy of a molecular system is equal to the negative of the orbital energy of the highest occupied molecular orbital (HOMO). This theorem is named after Tjalling Koopmans, who published this result in 1934.

Quantum Monte Carlo encompasses a large family of computational methods whose common aim is the study of complex quantum systems. One of the major goals of these approaches is to provide a reliable solution of the quantum many-body problem. The diverse flavors of quantum Monte Carlo approaches all share the common use of the Monte Carlo method to handle the multi-dimensional integrals that arise in the different formulations of the many-body problem.

<span class="mw-page-title-main">SIESTA (computer program)</span>

SIESTA is an original method and its computer program implementation, to efficiently perform electronic structure calculations and ab initio molecular dynamics simulations of molecules and solids. SIESTA uses strictly localized basis sets and the implementation of linear-scaling algorithms. Accuracy and speed can be set in a wide range, from quick exploratory calculations to highly accurate simulations matching the quality of other approaches, such as the plane-wave and all-electron methods.

General Atomic and Molecular Electronic Structure System (GAMESS (US)) is computer software for computational chemistry. The original code started on October 1, 1977 as a National Resources for Computations in Chemistry project. In 1981, the code base split into GAMESS (US) and GAMESS (UK) variants, which now differ significantly. GAMESS (US) is maintained by the members of the Gordon Research Group at Iowa State University. GAMESS (US) source code is available as source-available freeware, but is not open-source software, due to license restrictions.

<span class="mw-page-title-main">Spartan (chemistry software)</span>

Spartan is a molecular modelling and computational chemistry application from Wavefunction. It contains code for molecular mechanics, semi-empirical methods, ab initio models, density functional models, post-Hartree–Fock models, and thermochemical recipes including G3(MP2) and T1. Quantum chemistry calculations in Spartan are powered by Q-Chem.

Ab initio quantum chemistry methods are computational chemistry methods based on quantum chemistry. The term ab initio was first used in quantum chemistry by Robert Parr and coworkers, including David Craig in a semiempirical study on the excited states of benzene. The background is described by Parr. Ab initio means "from first principles" or "from the beginning", implying that the only inputs into an ab initio calculation are physical constants. Ab initio quantum chemistry methods attempt to solve the electronic Schrödinger equation given the positions of the nuclei and the number of electrons in order to yield useful information such as electron densities, energies and other properties of the system. The ability to run these calculations has enabled theoretical chemists to solve a range of problems and their importance is highlighted by the awarding of the Nobel prize to John Pople and Walter Kohn.

Car–Parrinello molecular dynamics or CPMD refers to either a method used in molecular dynamics or the computational chemistry software package used to implement this method.

Quantum chemistry composite methods are computational chemistry methods that aim for high accuracy by combining the results of several calculations. They combine methods with a high level of theory and a small basis set with methods that employ lower levels of theory with larger basis sets. They are commonly used to calculate thermodynamic quantities such as enthalpies of formation, atomization energies, ionization energies and electron affinities. They aim for chemical accuracy which is usually defined as within 1 kcal/mol of the experimental value. The first systematic model chemistry of this type with broad applicability was called Gaussian-1 (G1) introduced by John Pople. This was quickly replaced by the Gaussian-2 (G2) which has been used extensively. The Gaussian-3 (G3) was introduced later.

In computational chemistry, spin contamination is the artificial mixing of different electronic spin-states. This can occur when an approximate orbital-based wave function is represented in an unrestricted form – that is, when the spatial parts of α and β spin-orbitals are permitted to differ. Approximate wave functions with a high degree of spin contamination are undesirable. In particular, they are not eigenfunctions of the total spin-squared operator, Ŝ2, but can formally be expanded in terms of pure spin states of higher multiplicities.

<span class="mw-page-title-main">Molecular modeling on GPUs</span> Using graphics processing units for molecular simulations

Molecular modeling on GPU is the technique of using a graphics processing unit (GPU) for molecular simulations.

<span class="mw-page-title-main">Ascalaph Designer</span>

Ascalaph Designer is a computer program for general purpose molecular modelling for molecular design and simulations. It provides a graphical environment for the common programs of quantum and classical molecular modelling ORCA, NWChem, Firefly, CP2K and MDynaMix . The molecular mechanics calculations cover model building, energy optimizations and molecular dynamics. Firefly covers a wide range of quantum chemistry methods. Ascalaph Designer is free and open-source software, released under the GNU General Public License, version 2 (GPLv2).

In computational chemistry, a solvent model is a computational method that accounts for the behavior of solvated condensed phases. Solvent models enable simulations and thermodynamic calculations applicable to reactions and processes which take place in solution. These include biological, chemical and environmental processes. Such calculations can lead to new predictions about the physical processes occurring by improved understanding.

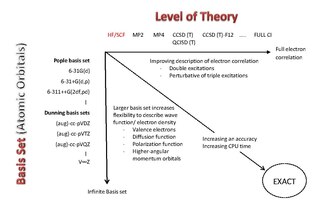
<span class="mw-page-title-main">Pople diagram</span> Diagram used in computational chemistry

A Pople diagram or Pople's Diagram is a diagram which describes the relationship between various calculation methods in computational chemistry. It was initially introduced in January 1965 by Sir John Pople,, during the Symposium of Atomic and Molecular Quantum Theory in Florida. The Pople Diagram can be either 2-dimensional or 3-dimensional, with the axes representing ab initio methods, basis sets and treatment of relativity. The diagram attempts to balance calculations by giving all aspects of a computation equal weight.

References

  1. ↑ K. Kitaura; E. Ikeo; T. Asada; T. Nakano; M. Uebayasi (1999). "Fragment molecular orbital method: an approximate computational method for large molecules". Chem. Phys. Lett. 313 (3–4): 701–706. Bibcode:1999CPL...313..701K. doi:10.1016/S0009-2614(99)00874-X.
  2. ↑ P. Otto; J. Ladik (1975). "Investigation of the interaction between molecules at medium distances: I. SCF LCAO MO supermolecule, perturbational and mutually consistent calculations for two interacting HF and CH2O molecules". Chem. Phys. 8 (1–2): 192–200. Bibcode:1975CP......8..192O. doi:10.1016/0301-0104(75)80107-8.
  3. ↑ Stoll, Hermann (1992). "Correlation energy of diamond". Physical Review B. 46 (11): 6700–6704. Bibcode:1992PhRvB..46.6700S. doi:10.1103/PhysRevB.46.6700. PMID   10002370.
  4. ↑ Huang, Lulu; Massa, Lou; Karle, Jerome (2005). "Kernel energy method illustrated with peptides". International Journal of Quantum Chemistry. Wiley. 103 (6): 808–817. Bibcode:2005IJQC..103..808H. doi:10.1002/qua.20542. ISSN   0020-7608.
  5. ↑ Dahlke, Erin E.; Truhlar, Donald G. (2006-11-04). "Electrostatically Embedded Many-Body Expansion for Large Systems, with Applications to Water Clusters". Journal of Chemical Theory and Computation. American Chemical Society (ACS). 3 (1): 46–53. CiteSeerX   10.1.1.186.8799 . doi:10.1021/ct600253j. ISSN   1549-9618. PMID   26627150.
  6. ↑ Hirata, So; Valiev, Marat; Dupuis, Michel; Xantheas, Sotiris S.; Sugiki, Shinichiro; Sekino, Hideo (2005-08-10). "Fast electron correlation methods for molecular clusters in the ground and excited states". Molecular Physics. Informa UK Limited. 103 (15–16): 2255–2265. Bibcode:2005MolPh.103.2255H. doi:10.1080/00268970500083788. ISSN   0026-8976. S2CID   95428135.
  7. ↑ Kamiya, Muneaki; Hirata, So; Valiev, Marat (2008-02-21). "Fast electron correlation methods for molecular clusters without basis set superposition errors". The Journal of Chemical Physics. AIP Publishing. 128 (7): 074103. Bibcode:2008JChPh.128g4103K. doi:10.1063/1.2828517. ISSN   0021-9606. PMID   18298136.
  8. ↑ Gordon, Mark S.; Fedorov, Dmitri G.; Pruitt, Spencer R.; Slipchenko, Lyudmila V. (2011-08-26). "Fragmentation Methods: A Route to Accurate Calculations on Large Systems". Chemical Reviews. American Chemical Society (ACS). 112 (1): 632–672. doi:10.1021/cr200093j. ISSN   0009-2665. PMID   21866983.
  9. ↑ The Fragment Molecular Orbital Method: Practical Applications to Large Molecular Systems, edited by D. G. Fedorov, K. Kitaura, CRC Press, Boca Raton, Florida, 2009 ISBN   978-1-4200-7848-0
  10. ↑ "(a) D. G. Fedorov, K. Kitaura, Theoretical development of the fragment molecular orbital (FMO) method and (b) T. Nakano, Y. Mochizuki, K. Fukuzawa, S. Amari, S. Tanaka, Developments and applications of ABINIT-MP software based on the fragment molecular orbital method in Modern methods for theoretical physical chemistry of biopolymers, edited by E. Starikov, J. Lewis, S. Tanaka, Elsevier, Amsterdam, 2006, ISBN   978-0-444-52220-7
  11. ↑ T. Nagata, D. G. Fedorov, K. Kitaura (2011). "Mathematical Formulation of the fragment molecular orbital method" in Linear-Scaling Techniques in Computational Chemistry and Physics. R. Zalesny, M. G. Papadopoulos, P. G. Mezey, J. Leszczyński (Eds.), Springer, New York, pp. 17-64.
  12. ↑ Y. Komeiji, Y. Mochizuki, T. Nakano, H. Mori (2012). "Recent advances in fragment molecular orbital-based molecular dynamics (FMO-MD) simulations", in Molecular Dynamics - Theoretical Developments and Applications in Nanotechnology and Energy, L. Wang (Ed.), Intech, pp. 3-24.
  13. ↑ Quantum mechanics in drug discovery., edited by A. Heifetz, Springer, New York, 2020 ISBN   978-1-0716-0281-2
  14. ↑ "日本化学会情報化学部会誌".
  15. ↑ "FMO@Fugaku". YouTube .
  16. ↑ "FMO@Summit". 18 November 2022. pp. 1–14.
  17. ↑ D. G. Fedorov; et al. (2007). "Extending the Power of Quantum Chemistry to Large Systems with the Fragment Molecular Orbital Method". J. Phys. Chem. A. 111 (30): 6904–6914. Bibcode:2007JPCA..111.6904F. doi:10.1021/jp0716740. PMID   17511437.
  18. ↑ Fedorov, Dmitri G.; Nagata, Takeshi; Kitaura, Kazuo (2012). "Exploring chemistry with the fragment molecular orbital method". Physical Chemistry Chemical Physics. Royal Society of Chemistry (RSC). 14 (21): 7562–7577. Bibcode:2012PCCP...14.7562F. doi:10.1039/c2cp23784a. ISSN   1463-9076. PMID   22410762.
  19. ↑ Tanaka, Shigenori; Mochizuki, Yuji; Komeiji, Yuto; Okiyama, Yoshio; Fukuzawa, Kaori (2014). "Electron-correlated fragment-molecular-orbital calculations for biomolecular and nano systems". Phys. Chem. Chem. Phys. Royal Society of Chemistry (RSC). 16 (22): 10310–10344. Bibcode:2014PCCP...1610310T. doi:10.1039/c4cp00316k. ISSN   1463-9076. PMID   24740821.
  20. ↑ Fedorov, Dmitri G. (2017). "The fragment molecular orbital method: theoretical development, implementation in GAMESS, and applications". WIREs Comput. Mol. Sci. 7 (6): e1322. doi:10.1002/wcms.1322. S2CID   103065280.
  21. ↑ Fukuzawa, Kaori; Tanaka, Shigenori (2022). "Fragment molecular orbital calculations for biomolecules". Current Opinion Structural Biology. 72: 127–134. doi: 10.1016/j.sbi.2021.08.010 . PMID   34656048. S2CID   239010379.
  22. ↑ Recent advances of the fragment molecular orbital method, edited by Y. Mochizuki, S. Tanaka, K. Fukuzawa, Springer, Singapore, 2021 ISBN   978-981-15-9234-8
  23. ↑ Complete guide to the fragment molecular orbital method in GAMESS., D. G. Fedorov, World Scientific, Singapore, 2023 ISBN   978-981-126-362-0
  24. ↑ "FMO consortium".
  25. ↑ http://staff.aist.go.jp/d.g.fedorov/fmo/fmoref.txt [ bare URL plain text file ]
  26. ↑ "ABINIT-MP (in Japanese)".
  27. ↑ "PAICS".
  28. ↑ "OpenFMO". GitHub .
  29. ↑ "fu". GitHub .
  30. ↑ "Facio the 3D-Molecular Modeling Software".
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.