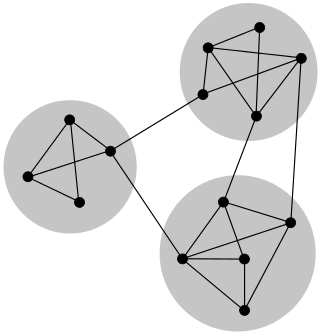
In graph theory, a component of an undirected graph is a connected subgraph that is not part of any larger connected subgraph. The components of any graph partition its vertices into disjoint sets, and are the induced subgraphs of those sets. A graph that is itself connected has exactly one component, consisting of the whole graph. Components are sometimes called connected components.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.

In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.
In the mathematical field of graph theory, a snark is an undirected graph with exactly three edges per vertex whose edges cannot be colored with only three colors. In order to avoid trivial cases, snarks are often restricted to have additional requirements on their connectivity and on the length of their cycles. Infinitely many snarks exist.
In the mathematical theory of matroids, a graphic matroid is a matroid whose independent sets are the forests in a given finite undirected graph. The dual matroids of graphic matroids are called co-graphic matroids or bond matroids. A matroid that is both graphic and co-graphic is sometimes called a planar matroid ; these are exactly the graphic matroids formed from planar graphs.
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements that need to be removed to separate the remaining nodes into two or more isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network.

In graph theory, a graph property or graph invariant is a property of graphs that depends only on the abstract structure, not on graph representations such as particular labellings or drawings of the graph.

In the mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a graph polynomial. It is a polynomial in two variables which plays an important role in graph theory. It is defined for every undirected graph and contains information about how the graph is connected. It is denoted by .
In graph theory, a Moore graph is a regular graph whose girth is more than twice its diameter. If the degree of such a graph is d and its diameter is k, its girth must equal 2k + 1. This is true, for a graph of degree d and diameter k, if and only if its number of vertices equals
In graph theory, a connected graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.

In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally independent graphs.
In the mathematical area of graph theory, the Mycielskian or Mycielski graph of an undirected graph is a larger graph formed from it by a construction of Jan Mycielski (1955). The construction preserves the property of being triangle-free but increases the chromatic number; by applying the construction repeatedly to a triangle-free starting graph, Mycielski showed that there exist triangle-free graphs with arbitrarily large chromatic number.

In the mathematical field of graph theory, the Grötzsch graph is a triangle-free graph with 11 vertices, 20 edges, chromatic number 4, and crossing number 5. It is named after German mathematician Herbert Grötzsch, who used it as an example in connection with his 1959 theorem that planar triangle-free graphs are 3-colorable.

In the mathematical area of graph theory, a cage is a regular graph that has as few vertices as possible for its girth.
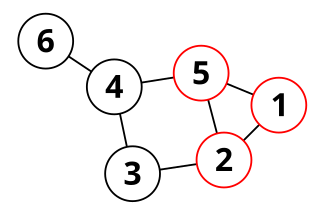
In graph theory, a peripheral cycle in an undirected graph is, intuitively, a cycle that does not separate any part of the graph from any other part. Peripheral cycles were first studied by Tutte (1963), and play important roles in the characterization of planar graphs and in generating the cycle spaces of nonplanar graphs.

In the mathematical field of graph theory, the Chvátal graph is an undirected graph with 12 vertices and 24 edges, discovered by Václav Chvátal in 1970. It is the smallest graph that is triangle-free, 4-regular, and 4-chromatic.
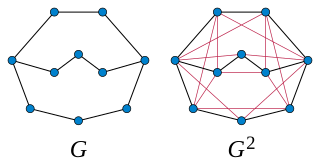
In graph theory, a branch of mathematics, the kth powerGk of an undirected graph G is another graph that has the same set of vertices, but in which two vertices are adjacent when their distance in G is at most k. Powers of graphs are referred to using terminology similar to that of exponentiation of numbers: G2 is called the square of G, G3 is called the cube of G, etc.
In matroid theory, a mathematical discipline, the girth of a matroid is the size of its smallest circuit or dependent set. The cogirth of a matroid is the girth of its dual matroid. Matroid girth generalizes the notion of the shortest cycle in a graph, the edge connectivity of a graph, Hall sets in bipartite graphs, even sets in families of sets, and general position of point sets. It is hard to compute, but fixed-parameter tractable for linear matroids when parameterized both by the matroid rank and the field size of a linear representation.