Global element

Last updated June 25, 2021

In category theory, a global element of an object A from a category is a morphism

h\colon 1\to A,

where $1$ is a terminal object of the category.^[1] Roughly speaking, global elements are a generalization of the notion of "elements" from the category of sets, and they can be used to import set-theoretic concepts into category theory. However, unlike a set, an object of a general category need not be determined by its global elements (not even up to isomorphism). For example, the terminal object of the category Grph of graph homomorphisms has one vertex and one edge, a self-loop,^[2] whence the global elements of a graph are its self-loops, conveying no information either about other kinds of edges, or about vertices having no self-loop, or about whether two self-loops share a vertex.

In an elementary topos the global elements of the subobject classifier $Ω$ form a Heyting algebra when ordered by inclusion of the corresponding subobjects of the terminal object.^[3] For example, Grph happens to be a topos, whose subobject classifier $Ω$ is a two-vertex directed clique with an additional self-loop (so five edges, three of which are self-loops and hence the global elements of $Ω$ ). The internal logic of Grph is therefore based on the three-element Heyting algebra as its truth values.

A well-pointed category is a category that has enough global elements to distinguish every two morphisms. That is, for each pair of distinct arrows $A \to B$ in the category, there should exist a global element whose compositions with them are different from each other.^[1]

Related Research Articles

Category theory formalizes mathematical structure and its concepts in terms of a labeled directed graph called a category, whose nodes are called objects, and whose labelled directed edges are called arrows. A category has two basic properties: the ability to compose the arrows associatively, and the existence of an identity arrow for each object. The language of category theory has been used to formalize concepts of other high-level abstractions such as sets, rings, and groups. Informally, category theory is a general theory of functions.

In mathematics, the power set of a set $S$ is the set of all subsets of $S$ , including the empty set and $S$ itself. In axiomatic set theory, the existence of the power set of any set is postulated by the axiom of power set. The powerset of $S$ is variously denoted as P( $S$ ), 𝒫( $S$ ), $P (S)$ , $(S), ℘(S), or 2 S . The notation 2 S is used because given any set with exactly two elements, the powerset of S can be identified with the set of all functions from S into that set.$

In mathematics, pointless topology is an approach to topology that avoids mentioning points, and which the lattices of open sets are the primitive notions in it.

In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are the total functions from A to B, and the composition of morphisms is the composition of functions.

In mathematics, an algebraic structure consists of a nonempty set A, a collection of operations on A of finite arity, and a finite set of identities, known as axioms, that these operations must satisfy.

In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth.

In mathematics, a Heyting algebra is a bounded lattice equipped with a binary operation a → b of implication such that ≤ b is equivalent to c ≤. From a logical standpoint, A → B is by this definition the weakest proposition for which modus ponens, the inference rule A → B, A ⊢ B, is sound. Like Boolean algebras, Heyting algebras form a variety axiomatizable with finitely many equations. Heyting algebras were introduced by Arend Heyting (1930) to formalize intuitionistic logic.

Graph (discrete mathematics) Mathematical structure consisting of vertices and edges connecting some pairs of vertices

In mathematics, and more specifically in graph theory, a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related". The objects correspond to mathematical abstractions called vertices and each of the related pairs of vertices is called an edge. Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. Graphs are one of the objects of study in discrete mathematics.

The following outline is provided as an overview of and guide to category theory, the area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows, where these collections satisfy certain basic conditions. Many significant areas of mathematics can be formalised as categories, and the use of category theory allows many intricate and subtle mathematical results in these fields to be stated, and proved, in a much simpler way than without the use of categories.

In mathematics, a quiver is a directed graph where loops and multiple arrows between two vertices are allowed, i.e. a multidigraph. They are commonly used in representation theory: a representation V of a quiver assigns a vector space V(x) to each vertex x of the quiver and a linear map V(a) to each arrow a.

In category theory, a subobject classifier is a special object Ω of a category such that, intuitively, the subobjects of any object X in the category correspond to the morphisms from X to Ω. In typical examples, that morphism assigns "true" to the elements of the subobject and "false" to the other elements of X. Therefore, a subobject classifier is also known as a "truth value object" and the concept is widely used in the categorical description of logic. Note however that subobject classifiers are often much more complicated than the simple binary logic truth values {true, false}.

In mathematics, there is an ample supply of categorical dualities between certain categories of topological spaces and categories of partially ordered sets. Today, these dualities are usually collected under the label Stone duality, since they form a natural generalization of Stone's representation theorem for Boolean algebras. These concepts are named in honor of Marshall Stone. Stone-type dualities also provide the foundation for pointless topology and are exploited in theoretical computer science for the study of formal semantics.

In category theory, a branch of mathematics, a subobject is, roughly speaking, an object that sits inside another object in the same category. The notion is a generalization of concepts such as subsets from set theory, subgroups from group theory, and subspaces from topology. Since the detailed structure of objects is immaterial in category theory, the definition of subobject relies on a morphism that describes how one object sits inside another, rather than relying on the use of elements.

In mathematics, a duality translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. Such involutions sometimes have fixed points, so that the dual of A is A itself. For example, Desargues' theorem is self-dual in this sense under the standard duality in projective geometry.

In mathematics, a simplicial set is an object made up of "simplices" in a specific way. Simplicial sets are higher-dimensional generalizations of directed graphs, partially ordered sets and categories. Formally, a simplicial set may be defined as a contravariant functor from the simplex category to the category of sets. Simplicial sets were introduced in 1950 by Samuel Eilenberg and J. A. Zilber.

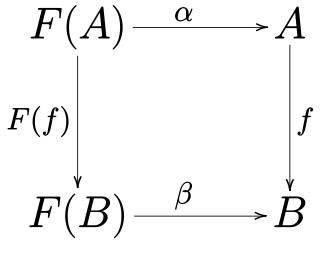
In mathematics, specifically in category theory, F-algebras generalize the notion of algebraic structure. Rewriting the algebraic laws in terms of morphisms eliminates all references to quantified elements from the axioms, and these algebraic laws may then be glued together in terms of a single functor F, the signature.

In mathematics, a representation is a very general relationship that expresses similarities between mathematical objects or structures. Roughly speaking, a collection Y of mathematical objects may be said to represent another collection X of objects, provided that the properties and relationships existing among the representing objects y_i conform, in some consistent way, to those existing among the corresponding represented objects x_i. More specifically, given a set Π of properties and relations, a Π-representation of some structure X is a structure Y that is the image of X under a homomorphism that preserves Π. The label representation is sometimes also applied to the homomorphism itself.

In mathematics, a topos is a category that behaves like the category of sheaves of sets on a topological space. Topoi behave much like the category of sets and possess a notion of localization; they are a direct generalization of point-set topology. The Grothendieck topoi find applications in algebraic geometry; the more general elementary topoi are used in logic.

In mathematics, a Lawvere–Tierney topology is an analog of a Grothendieck topology for an arbitrary topos, used to construct a topos of sheaves. A Lawvere–Tierney topology is also sometimes also called a local operator or coverage or topology or geometric modality. They were introduced by William Lawvere (1971) and Myles Tierney.

In mathematics, specifically category theory, a quasitopos is a generalization of a topos. A topos has a subobject classifier classifying all subobjects, but in a quasitopos, only strong subobjects are classified. Quasitoposes are also required to be finitely cocomplete and locally cartesian closed. A solid quasitopos is one for which 0 is a strong subobject of 1.

References

1 2 Mac Lane, Saunders; Moerdijk, Ieke (1992), Sheaves in geometry and logic: A first introduction to topos theory, Universitext, New York: Springer-Verlag, p. 236, ISBN 0-387-97710-4, MR 1300636 .
↑ Gray, John W. (1989), "The category of sketches as a model for algebraic semantics", Categories in computer science and logic (Boulder, CO, 1987), Contemp. Math., 92, Amer. Math. Soc., Providence, RI, pp. 109–135, doi:10.1090/conm/092/1003198, MR 1003198 .
↑ Nourani, Cyrus F. (2014), A functorial model theory: Newer applications to algebraic topology, descriptive sets, and computing categories topos, Toronto, ON: Apple Academic Press, p. 38, doi:10.1201/b16416, ISBN 978-1-926895-92-5, MR 3203114 .

This category theory-related article is a stub. You can help Wikipedia by expanding it.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[mm-1] 1 2 Mac Lane, Saunders; Moerdijk, Ieke (1992), Sheaves in geometry and logic: A first introduction to topos theory, Universitext, New York: Springer-Verlag, p. 236, ISBN 0-387-97710-4, MR 1300636 .

[2] Gray, John W. (1989), "The category of sketches as a model for algebraic semantics", Categories in computer science and logic (Boulder, CO, 1987), Contemp. Math., 92, Amer. Math. Soc., Providence, RI, pp. 109–135, doi:10.1090/conm/092/1003198, MR 1003198 .

[3] Nourani, Cyrus F. (2014), A functorial model theory: Newer applications to algebraic topology, descriptive sets, and computing categories topos, Toronto, ON: Apple Academic Press, p. 38, doi:10.1201/b16416, ISBN 978-1-926895-92-5, MR 3203114 .

[1]

[2]

[3]