Glossary of tensor theory

Last updated January 12, 2023

This is a glossary of tensor theory. For expositions of tensor theory from different points of view, see:

Classical notation

Ricci calculus: The earliest foundation of tensor theory – tensor index notation.^[1]

Order of a tensor: The components of a tensor with respect to a basis is an indexed array. The order of a tensor is the number of indices needed. Some texts may refer to the tensor order using the term degree or rank.

Rank of a tensor: The rank of a tensor is the minimum number of rank-one tensor that must be summed to obtain the tensor. A rank-one tensor may be defined as expressible as the outer product of the number of nonzero vectors needed to obtain the correct order.

Dyadic tensor: A dyadic tensor is a tensor of order two, and may be represented as a square matrix. In contrast, a dyad is specifically a dyadic tensor of rank one.

Einstein notation: This notation is based on the understanding that whenever a multidimensional array contains a repeated index letter, the default interpretation is that the product is summed over all permitted values of the index. For example, if a_ij is a matrix, then under this convention a_ii is its trace. The Einstein convention is widely used in physics and engineering texts, to the extent that if summation is not to be applied, it is normal to note that explicitly.

Kronecker delta

Levi-Civita symbol

Covariant tensor

Contravariant tensor: The classical interpretation is by components. For example, in the differential form a_idxⁱ the componentsa_i are a covariant vector. That means all indices are lower; contravariant means all indices are upper.

Mixed tensor: This refers to any tensor that has both lower and upper indices.

Cartesian tensor: Cartesian tensors are widely used in various branches of continuum mechanics, such as fluid mechanics and elasticity. In classical continuum mechanics, the space of interest is usually 3-dimensional Euclidean space, as is the tangent space at each point. If we restrict the local coordinates to be Cartesian coordinates with the same scale centered at the point of interest, the metric tensor is the Kronecker delta. This means that there is no need to distinguish covariant and contravariant components, and furthermore there is no need to distinguish tensors and tensor densities. All Cartesian-tensor indices are written as subscripts. Cartesian tensors achieve considerable computational simplification at the cost of generality and of some theoretical insight.

Contraction of a tensor

Raising and lowering indices

Symmetric tensor

Antisymmetric tensor

Multiple cross products

Algebraic notation

This avoids the initial use of components, and is distinguished by the explicit use of the tensor product symbol.

Tensor product

If v and w are vectors in vector spaces V and W respectively, then

v\otimes w

is a tensor in

V\otimes W.

That is, the ⊗ operation is a binary operation, but it takes values into a fresh space (it is in a strong sense external). The ⊗ operation is a bilinear map; but no other conditions are applied to it.

Pure tensor: A pure tensor of V⊗W is one that is of the form v⊗w.; It could be written dyadically aⁱb^j, or more accurately aⁱb^je_i⊗f_j, where the e_i are a basis for V and the f_j a basis for W. Therefore, unless V and W have the same dimension, the array of components need not be square. Such pure tensors are not generic: if both V and W have dimension greater than 1, there will be tensors that are not pure, and there will be non-linear conditions for a tensor to satisfy, to be pure. For more see Segre embedding.

Tensor algebra: In the tensor algebra T(V) of a vector space V, the operation $\otimes$ becomes a normal (internal) binary operation. A consequence is that T(V) has infinite dimension unless V has dimension 0. The free algebra on a set X is for practical purposes the same as the tensor algebra on the vector space with X as basis.

Hodge star operator

Exterior power

The wedge product is the anti-symmetric form of the ⊗ operation. The quotient space of T(V) on which it becomes an internal operation is the exterior algebra of V; it is a graded algebra, with the graded piece of weight k being called the k-th exterior power of V.

Symmetric power, symmetric algebra: This is the invariant way of constructing polynomial algebras.

Applications

Metric tensor

Strain tensor

Stress–energy tensor

Tensor field theory

Jacobian matrix

Tensor field

Tensor density

Lie derivative

Tensor derivative

Differential geometry

Abstract algebra

Tensor product of fields: This is an operation on fields, that does not always produce a field.

Tensor product of R-algebras

Clifford module: A representation of a Clifford algebra which gives a realisation of a Clifford algebra as a matrix algebra.

Tor functors: These are the derived functors of the tensor product, and feature strongly in homological algebra. The name comes from the torsion subgroup in abelian group theory.

Symbolic method of invariant theory

Derived category

Grothendieck's six operations: These are highly abstract approaches used in some parts of geometry.

Spinors

See:

Spin group

Spin-c group

Spinor

Pin group

Pinors

Spinor field

Killing spinor

Spin manifold

Related Research Articles

In mathematics, a product is the result of multiplication, or an expression that identifies objects to be multiplied, called factors. For example, 30 is the product of 6 and 5, and $is the product of and .$

In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Tensors may map between different objects such as vectors, scalars, and even other tensors. There are many types of tensors, including scalars and vectors, dual vectors, multilinear maps between vector spaces, and even some operations such as the dot product. Tensors are defined independent of any basis, although they are often referred to by their components in a basis related to a particular coordinate system.

In mathematics, the tensor product $of two vector spaces V and W is a vector space to which is associated a bilinear map that maps a pair to an element of denoted$

In linear algebra, the outer product of two coordinate vectors is a matrix. If the two vectors have dimensions n and m, then their outer product is an n × m matrix. More generally, given two tensors, their outer product is a tensor. The outer product of tensors is also referred to as their tensor product, and can be used to define the tensor algebra.

In mathematics, especially the usage of linear algebra in Mathematical physics, Einstein notation is a notational convention that implies summation over a set of indexed terms in a formula, thus achieving brevity. As part of mathematics it is a notational subset of Ricci calculus; however, it is often used in physics applications that do not distinguish between tangent and cotangent spaces. It was introduced to physics by Albert Einstein in 1916.

In the mathematical field of differential geometry, a metric tensor is an additional structure on a manifold $M$ that allows defining distances and angles, just as the inner product on a Euclidean space allows defining distances and angles there. More precisely, a metric tensor at a point $p$ of $M$ is a bilinear form defined on the tangent space at $p$ , and a metric tensor on $M$ consists of a metric tensor at each point $p$ of $M$ that varies smoothly with $p$ .

In multilinear algebra, a tensor contraction is an operation on a tensor that arises from the natural pairing of a finite-dimensional vector space and its dual. In components, it is expressed as a sum of products of scalar components of the tensor(s) caused by applying the summation convention to a pair of dummy indices that are bound to each other in an expression. The contraction of a single mixed tensor occurs when a pair of literal indices of the tensor are set equal to each other and summed over. In Einstein notation this summation is built into the notation. The result is another tensor with order reduced by 2.

In physics, especially in multilinear algebra and tensor analysis, covariance and contravariance describe how the quantitative description of certain geometric or physical entities changes with a change of basis. In modern mathematical notation, the role is sometimes swapped.

In mathematical physics, Minkowski space combines inertial space and time manifolds (x,y) with a non-inertial reference frame of space and time (x',t') into a four-dimensional model relating a position to the field (physics). A four-vector (x,y,z,t) consisting of coordinate axes such as a Euclidean space plus time may be used with the non-inertial frame to illustrate specifics of motion, but should not be confused with the spacetime model generally. The model helps show how a spacetime interval between any two events is independent of the inertial frame of reference in which they are recorded. Although initially developed by mathematician Hermann Minkowski for Maxwell's equations of electromagnetism, the mathematical structure of Minkowski spacetime was shown to be implied by the postulates of special relativity.

In mathematics, the modern component-free approach to the theory of a tensor views a tensor as an abstract object, expressing some definite type of multilinear concept. Their properties can be derived from their definitions, as linear maps or more generally; and the rules for manipulations of tensors arise as an extension of linear algebra to multilinear algebra.

In mathematics and physics, a tensor field assigns a tensor to each point of a mathematical space. Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical sciences. As a tensor is a generalization of a scalar and a vector, a tensor field is a generalization of a scalar field or vector field that assigns, respectively, a scalar or vector to each point of space. If a tensor $A$ is defined on a vector fields set $X(M)$ over a module $M$ , we call $A$ a tensor field on $M$ .

In mathematics, tensor calculus, tensor analysis, or Ricci calculus is an extension of vector calculus to tensor fields.

In mathematics and theoretical physics, a tensor is antisymmetric onan index subset if it alternates sign (+/−) when any two indices of the subset are interchanged. The index subset must generally either be all covariant or all contravariant.

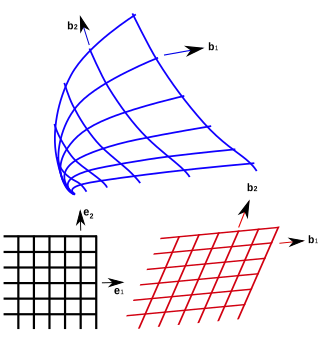
In geometry, curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible at each point. This means that one can convert a point given in a Cartesian coordinate system to its curvilinear coordinates and back. The name curvilinear coordinates, coined by the French mathematician Lamé, derives from the fact that the coordinate surfaces of the curvilinear systems are curved.

Abstract index notation is a mathematical notation for tensors and spinors that uses indices to indicate their types, rather than their components in a particular basis. The indices are mere placeholders, not related to any basis and, in particular, are non-numerical. Thus it should not be confused with the Ricci calculus. The notation was introduced by Roger Penrose as a way to use the formal aspects of the Einstein summation convention to compensate for the difficulty in describing contractions and covariant differentiation in modern abstract tensor notation, while preserving the explicit covariance of the expressions involved.

When studying and formulating Albert Einstein's theory of general relativity, various mathematical structures and techniques are utilized. The main tools used in this geometrical theory of gravitation are tensor fields defined on a Lorentzian manifold representing spacetime. This article is a general description of the mathematics of general relativity.

In mathematics, a metric connection is a connection in a vector bundle E equipped with a bundle metric; that is, a metric for which the inner product of any two vectors will remain the same when those vectors are parallel transported along any curve. This is equivalent to:

The mathematics of general relativity is complex. In Newton's theories of motion, an object's length and the rate at which time passes remain constant while the object accelerates, meaning that many problems in Newtonian mechanics may be solved by algebra alone. In relativity, however, an object's length and the rate at which time passes both change appreciably as the object's speed approaches the speed of light, meaning that more variables and more complicated mathematics are required to calculate the object's motion. As a result, relativity requires the use of concepts such as vectors, tensors, pseudotensors and curvilinear coordinates.

In mathematics, a symmetric tensor is a tensor that is invariant under a permutation of its vector arguments:

In mathematics, Ricci calculus constitutes the rules of index notation and manipulation for tensors and tensor fields on a differentiable manifold, with or without a metric tensor or connection. It is also the modern name for what used to be called the absolute differential calculus, developed by Gregorio Ricci-Curbastro in 1887–1896, and subsequently popularized in a paper written with his pupil Tullio Levi-Civita in 1900. Jan Arnoldus Schouten developed the modern notation and formalism for this mathematical framework, and made contributions to the theory, during its applications to general relativity and differential geometry in the early twentieth century.

References

↑ Ricci, Gregorio; Levi-Civita, Tullio (March 1900), "Méthodes de calcul différentiel absolu et leurs applications" [Absolute differential calculation methods & their applications], Mathematische Annalen (in French), Springer, 54 (1–2): 125–201, doi:10.1007/BF01454201, S2CID 120009332

Books

Bishop, R.L.; Goldberg, S.I. (1968), Tensor Analysis on Manifolds (First Dover 1980 ed.), The Macmillan Company, ISBN 0-486-64039-6
Danielson, Donald A. (2003). Vectors and Tensors in Engineering and Physics (2/e ed.). Westview (Perseus). ISBN 978-0-8133-4080-7.
Dimitrienko, Yuriy (2002). Tensor Analysis and Nonlinear Tensor Functions. Kluwer Academic Publishers (Springer). ISBN 1-4020-1015-X.
Lovelock, David; Hanno Rund (1989) [1975]. Tensors, Differential Forms, and Variational Principles. Dover. ISBN 978-0-486-65840-7.
Synge, John L; Schild, Alfred (1949). Tensor Calculus. Dover Publications 1978 edition. ISBN 978-0-486-63612-2.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Ricci, Gregorio; Levi-Civita, Tullio (March 1900), "Méthodes de calcul différentiel absolu et leurs applications" [Absolute differential calculation methods & their applications], Mathematische Annalen (in French), Springer, 54 (1–2): 125–201, doi:10.1007/BF01454201, S2CID 120009332

[1]