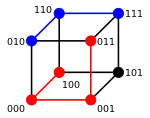
In computer science and telecommunication, Hamming codes are a family of linear error-correcting codes. Hamming codes can detect one-bit and two-bit errors, or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three. Richard W. Hamming invented Hamming codes in 1950 as a way of automatically correcting errors introduced by punched card readers. In his original paper, Hamming elaborated his general idea, but specifically focused on the Hamming(7,4) code which adds three parity bits to four bits of data.
Reed–Solomon codes are a group of error-correcting codes that were introduced by Irving S. Reed and Gustave Solomon in 1960. They have many applications, the most prominent of which include consumer technologies such as MiniDiscs, CDs, DVDs, Blu-ray discs, QR codes, data transmission technologies such as DSL and WiMAX, broadcast systems such as satellite communications, DVB and ATSC, and storage systems such as RAID 6.

Coding theory is the study of the properties of codes and their respective fitness for specific applications. Codes are used for data compression, cryptography, error detection and correction, data transmission and data storage. Codes are studied by various scientific disciplines—such as information theory, electrical engineering, mathematics, linguistics, and computer science—for the purpose of designing efficient and reliable data transmission methods. This typically involves the removal of redundancy and the correction or detection of errors in the transmitted data.
In coding theory, block codes are a large and important family of error-correcting codes that encode data in blocks. There is a vast number of examples for block codes, many of which have a wide range of practical applications. The abstract definition of block codes is conceptually useful because it allows coding theorists, mathematicians, and computer scientists to study the limitations of all block codes in a unified way. Such limitations often take the form of bounds that relate different parameters of the block code to each other, such as its rate and its ability to detect and correct errors.
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although turbo codes can be seen as a hybrid of these two types. Linear codes allow for more efficient encoding and decoding algorithms than other codes.
In coding theory, the Singleton bound, named after Richard Collom Singleton, is a relatively crude upper bound on the size of an arbitrary block code with block length , size and minimum distance . It is also known as the Joshibound. proved by Joshi (1958) and even earlier by Komamiya (1953).
In mathematics and computer science, in the field of coding theory, the Hamming bound is a limit on the parameters of an arbitrary block code: it is also known as the sphere-packing bound or the volume bound from an interpretation in terms of packing balls in the Hamming metric into the space of all possible words. It gives an important limitation on the efficiency with which any error-correcting code can utilize the space in which its code words are embedded. A code that attains the Hamming bound is said to be a perfect code.
In coding theory, decoding is the process of translating received messages into codewords of a given code. There have been many common methods of mapping messages to codewords. These are often used to recover messages sent over a noisy channel, such as a binary symmetric channel.
Reed–Muller codes are error-correcting codes that are used in wireless communications applications, particularly in deep-space communication. Moreover, the proposed 5G standard relies on the closely related polar codes for error correction in the control channel. Due to their favorable theoretical and mathematical properties, Reed–Muller codes have also been extensively studied in theoretical computer science.
In coding theory, the repetition code is one of the most basic linear error-correcting codes. In order to transmit a message over a noisy channel that may corrupt the transmission in a few places, the idea of the repetition code is to just repeat the message several times. The hope is that the channel corrupts only a minority of these repetitions. This way the receiver will notice that a transmission error occurred since the received data stream is not the repetition of a single message, and moreover, the receiver can recover the original message by looking at the received message in the data stream that occurs most often.

In statistics and coding theory, a Hamming space is usually the set of all binary strings of length N. It is used in the theory of coding signals and transmission.

In coding theory, a cyclic code is a block code, where the circular shifts of each codeword gives another word that belongs to the code. They are error-correcting codes that have algebraic properties that are convenient for efficient error detection and correction.
In coding theory, a constant-weight code, also called an m-of-n code, is an error detection and correction code where all codewords share the same Hamming weight. The one-hot code and the balanced code are two widely used kinds of constant-weight code.

In coding theory, Hamming(7,4) is a linear error-correcting code that encodes four bits of data into seven bits by adding three parity bits. It is a member of a larger family of Hamming codes, but the term Hamming code often refers to this specific code that Richard W. Hamming introduced in 1950. At the time, Hamming worked at Bell Telephone Laboratories and was frustrated with the error-prone punched card reader, which is why he started working on error-correcting codes.
Lexicographic codes or lexicodes are greedily generated error-correcting codes with remarkably good properties. They were produced independently by Vladimir Levenshtein and by John Horton Conway and Neil Sloane. The binary lexicographic codes are linear codes, and include the Hamming codes and the binary Golay codes.
The cyclic redundancy check (CRC) is based on division in the ring of polynomials over the finite field GF(2), that is, the set of polynomials where each coefficient is either zero or one, and arithmetic operations wrap around.
In coding theory, a polynomial code is a type of linear code whose set of valid code words consists of those polynomials that are divisible by a given fixed polynomial.
A locally decodable code (LDC) is an error-correcting code that allows a single bit of the original message to be decoded with high probability by only examining a small number of bits of a possibly corrupted codeword. This property could be useful, say, in a context where information is being transmitted over a noisy channel, and only a small subset of the data is required at a particular time and there is no need to decode the entire message at once. Note that locally decodable codes are not a subset of locally testable codes, though there is some overlap between the two.
AN codes are error-correcting code that are used in arithmetic applications. Arithmetic codes were commonly used in computer processors to ensure the accuracy of its arithmetic operations when electronics were more unreliable. Arithmetic codes help the processor to detect when an error is made and correct it. Without these codes, processors would be unreliable since any errors would go undetected. AN codes are arithmetic codes that are named for the integers and that are used to encode and decode the codewords.
In coding theory, burst error-correcting codes employ methods of correcting burst errors, which are errors that occur in many consecutive bits rather than occurring in bits independently of each other.