
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron.

Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry; Elements. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier, Euclid was the first to organize these propositions into a logical system in which each result is proved from axioms and previously proved theorems.
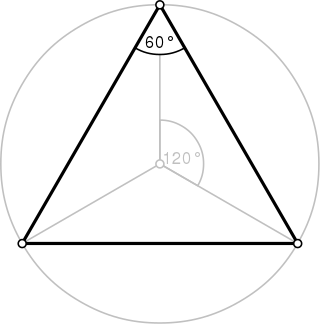
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted .

In geometry, two figures or objects are congruent if they have the same shape and size, or if one has the same shape and size as the mirror image of the other.

In Euclidean geometry, two objects are similar if they have the same shape, or if one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling, possibly with additional translation, rotation and reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruent to the result of a particular uniform scaling of the other.

In elementary geometry, two geometric objects are perpendicular if their intersection forms right angles at the point of intersection called a foot. The condition of perpendicularity may be represented graphically using the perpendicular symbol, ⟂. Perpendicular intersections can happen between two lines, between a line and a plane, and between two planes.

A shape or figure is a graphical representation of an object or its external boundary, outline, or external surface, as opposed to other properties such as color, texture, or material type. A plane shape or plane figure is constrained to lie on a plane, in contrast to solid 3D shapes. A two-dimensional shape or two-dimensional figure may lie on a more general curved surface.

Spherical geometry is the geometry of the two-dimensional surface of a sphere. Long studied for its practical applications – spherical trigonometry – to navigation, spherical geometry bears many similarities and relationships to, and important differences from, Euclidean plane geometry. The sphere has for the most part been studied as a part of 3-dimensional Euclidean geometry, the surface thought of as placed inside an ambient 3-d space. It can also be analyzed by "intrinsic" methods that only involve the surface itself, and do not refer to, or even assume the existence of, any surrounding space outside or inside the sphere.

A taxicab geometry or a Manhattan geometry is a geometry whose usual distance function or metric of Euclidean geometry is replaced by a new metric in which the distance between two points is the sum of the absolute differences of their Cartesian coordinates. The taxicab metric is also known as rectilinear distance, L1 distance, L1 distance or norm, snake distance, city block distance, Manhattan distance or Manhattan length. The latter names refer to the rectilinear street layout on the island of Manhattan, where the shortest path a taxi travels between two points is the sum of the absolute values of distances that it travels on avenues and on streets.
Hilbert's axioms are a set of 20 assumptions proposed by David Hilbert in 1899 in his book Grundlagen der Geometrie as the foundation for a modern treatment of Euclidean geometry. Other well-known modern axiomatizations of Euclidean geometry are those of Alfred Tarski and of George Birkhoff.

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.

In mathematics, an invariant is a property of a mathematical object which remains unchanged after operations or transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used. For example, the area of a triangle is an invariant with respect to isometries of the Euclidean plane. The phrases "invariant under" and "invariant to" a transformation are both used. More generally, an invariant with respect to an equivalence relation is a property that is constant on each equivalence class.

In mathematics, incidence geometry is the study of incidence structures. A geometric structure such as the Euclidean plane is a complicated object that involves concepts such as length, angles, continuity, betweenness, and incidence. An incidence structure is what is obtained when all other concepts are removed and all that remains is the data about which points lie on which lines. Even with this severe limitation, theorems can be proved and interesting facts emerge concerning this structure. Such fundamental results remain valid when additional concepts are added to form a richer geometry. It sometimes happens that authors blur the distinction between a study and the objects of that study, so it is not surprising to find that some authors refer to incidence structures as incidence geometries.

Elementary mathematics, also known as primary or secondary school school mathematics, is the study of mathematics topics that are commonly taught at the primary or secondary school levels around the world. It includes a wide range of mathematical concepts and skills, including number sense, algebra, geometry, measurement, and data analysis. These concepts and skills form the foundation for more advanced mathematical study and are essential for success in many fields and everyday life. The study of elementary mathematics is a crucial part of a student's education and lays the foundation for future academic and career success.
Tarski's axioms, due to Alfred Tarski, are an axiom set for the substantial fragment of Euclidean geometry that is formulable in first-order logic with identity, and requiring no set theory. Other modern axiomizations of Euclidean geometry are Hilbert's axioms and Birkhoff's axioms.

Geometric graph theory in the broader sense is a large and amorphous subfield of graph theory, concerned with graphs defined by geometric means. In a stricter sense, geometric graph theory studies combinatorial and geometric properties of geometric graphs, meaning graphs drawn in the Euclidean plane with possibly intersecting straight-line edges, and topological graphs, where the edges are allowed to be arbitrary continuous curves connecting the vertices, thus it is "the theory of geometric and topological graphs". Geometric graphs are also known as spatial networks.
The sector, also known as a proportional compass or military compass, was a major calculating instrument in use from the end of the sixteenth century until the nineteenth century. It is an instrument consisting of two rulers of equal length joined by a hinge. A number of scales are inscribed upon the instrument which facilitate various mathematical calculations. It was used for solving problems in proportion, multiplication and division, geometry, and trigonometry, and for computing various mathematical functions, such as square roots and cube roots. Its several scales permitted easy and direct solutions of problems in gunnery, surveying and navigation. The sector derives its name from the fourth proposition of the sixth book of Euclid, where it is demonstrated that similar triangles have their like sides proportional. Some sectors also incorporated a quadrant, and sometimes a clamp at the end of one leg which allowed the device to be used as a gunner's quadrant.

In mathematics, particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points whenever the distance between them is exactly one. To distinguish these graphs from a broader definition that allows some non-adjacent pairs of vertices to be at distance one, they may also be called strict unit distance graphs or faithful unit distance graphs. As a hereditary family of graphs, they can be characterized by forbidden induced subgraphs. The unit distance graphs include the cactus graphs, the matchstick graphs and penny graphs, and the hypercube graphs. The generalized Petersen graphs are non-strict unit distance graphs.
Foundations of geometry is the study of geometries as axiomatic systems. There are several sets of axioms which give rise to Euclidean geometry or to non-Euclidean geometries. These are fundamental to the study and of historical importance, but there are a great many modern geometries that are not Euclidean which can be studied from this viewpoint. The term axiomatic geometry can be applied to any geometry that is developed from an axiom system, but is often used to mean Euclidean geometry studied from this point of view. The completeness and independence of general axiomatic systems are important mathematical considerations, but there are also issues to do with the teaching of geometry which come into play.














