Hearing the shape of a drum

Last updated September 08, 2023

To hear the shape of a drum is to infer information about the shape of the drumhead from the sound it makes, i.e., from the list of overtones, via the use of mathematical theory.

"Can One Hear the Shape of a Drum?" is the title of a 1966 article by Mark Kac in the American Mathematical Monthly which made the question famous, though this particular phrasing originates with Lipman Bers. Similar questions can be traced back all the way to physicist Arthur Schuster in 1882.^[1] For his paper, Kac was given the Lester R. Ford Award in 1967 and the Chauvenet Prize in 1968.^[2]

The frequencies at which a drumhead can vibrate depend on its shape. The Helmholtz equation calculates the frequencies if the shape is known. These frequencies are the eigenvalues of the Laplacian in the space. A central question is whether the shape can be predicted if the frequencies are known; for example, whether a Reuleaux triangle can be recognized in this way.^[3] Kac admitted that he did not know whether it was possible for two different shapes to yield the same set of frequencies. The question of whether the frequencies determine the shape was finally answered in the negative in the early 1990s by Gordon, Webb and Wolpert.

Formal statement

More formally, the drum is conceived as an elastic membrane whose boundary is clamped. It is represented as a domain D in the plane. Denote by λ_n the Dirichlet eigenvalues for D: that is, the eigenvalues of the Dirichlet problem for the Laplacian:

{\begin{cases}\Delta u+\lambda u=0\\u|_{\partial D}=0\end{cases}}

Two domains are said to be isospectral (or homophonic) if they have the same eigenvalues. The term "homophonic" is justified because the Dirichlet eigenvalues are precisely the fundamental tones that the drum is capable of producing: they appear naturally as Fourier coefficients in the solution wave equation with clamped boundary.

Therefore, the question may be reformulated as: what can be inferred on D if one knows only the values of λ_n? Or, more specifically: are there two distinct domains that are isospectral?

Related problems can be formulated for the Dirichlet problem for the Laplacian on domains in higher dimensions or on Riemannian manifolds, as well as for other elliptic differential operators such as the Cauchy–Riemann operator or Dirac operator. Other boundary conditions besides the Dirichlet condition, such as the Neumann boundary condition, can be imposed. See spectral geometry and isospectral as related articles.

The answer

One-parameter family of isospectral drums Barabany.gif — One-parameter family of isospectral drums

In 1964, John Milnor observed that a theorem on lattices due to Ernst Witt implied the existence of a pair of 16-dimensional flat tori that have the same eigenvalues but different shapes. However, the problem in two dimensions remained open until 1992, when Carolyn Gordon, David Webb, and Scott Wolpert constructed, based on the Sunada method, a pair of regions in the plane that have different shapes but identical eigenvalues. The regions are concave polygons. The proof that both regions have the same eigenvalues uses the symmetries of the Laplacian. This idea has been generalized by Buser, Conway, Doyle, and Semmler^[4] who constructed numerous similar examples. So, the answer to Kac's question is: for many shapes, one cannot hear the shape of the drum completely. However, some information can be inferred.

On the other hand, Steve Zelditch proved that the answer to Kac's question is positive if one imposes restrictions to certain convex planar regions with analytic boundary. It is not known whether two non-convex analytic domains can have the same eigenvalues. It is known that the set of domains isospectral with a given one is compact in the C^∞ topology. Moreover, the sphere (for instance) is spectrally rigid, by Cheng's eigenvalue comparison theorem. It is also known, by a result of Osgood, Phillips, and Sarnak that the moduli space of Riemann surfaces of a given genus does not admit a continuous isospectral flow through any point, and is compact in the Fréchet–Schwartz topology.

Weyl's formula

Weyl's formula states that one can infer the area A of the drum by counting how rapidly the λ_n grow. We define N(R) to be the number of eigenvalues smaller than R and we get

A=\omega _{d}^{-1}(2\pi )^{d}\lim _{R\to \infty }{\frac {N(R)}{R^{d/2}}},

where d is the dimension, and $\omega _{d}$ is the volume of the d-dimensional unit ball. Weyl also conjectured that the next term in the approximation below would give the perimeter of D. In other words, if L denotes the length of the perimeter (or the surface area in higher dimension), then one should have

N(R)=(2\pi )^{-d}\omega _{d}AR^{d/2}\mp {\frac {1}{4}}(2\pi )^{-d+1}\omega _{d-1}LR^{(d-1)/2}+o(R^{(d-1)/2}).

For a smooth boundary, this was proved by Victor Ivrii in 1980. The manifold is also not allowed to have a two-parameter family of periodic geodesics, such as a sphere would have.

The Weyl–Berry conjecture

For non-smooth boundaries, Michael Berry conjectured in 1979 that the correction should be of the order of

R^{D/2},

where D is the Hausdorff dimension of the boundary. This was disproved by J. Brossard and R. A. Carmona, who then suggested that one should replace the Hausdorff dimension with the upper box dimension. In the plane, this was proved if the boundary has dimension 1 (1993), but mostly disproved for higher dimensions (1996); both results are by Lapidus and Pomerance.

Notes

↑ Crowell, Rachel (2022-06-28). "Mathematicians Are Trying to 'Hear' Shapes—And Reach Higher Dimensions". Scientific American. Retrieved 2022-11-15.
↑ "Can One Hear the Shape of a Drum? | Mathematical Association of America".
↑ Kac, Mark (April 1966). "Can One Hear the Shape of a Drum?" (PDF). American Mathematical Monthly . 73 (4, part 2): 16. doi:10.2307/2313748. JSTOR 2313748.
↑ Buser et al. 1994.
↑ Arrighetti, W.; Gerosa, G. (2005). Can you hear the fractal dimension of a drum?. pp. 65–75. arXiv: math.SP/0503748 . doi:10.1142/9789812701817_0007. ISBN 978-981-256-368-2. S2CID 119709456.{{cite book}}: |journal= ignored (help)

Related Research Articles

In the mathematical field of geometric topology, the Poincaré conjecture is a theorem about the characterization of the 3-sphere, which is the hypersphere that bounds the unit ball in four-dimensional space.

In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols $, (where is the nabla operator), or . In a Cartesian coordinate system, the Laplacian is given by the sum of second partial derivatives of the function with respect to each independent variable. In other coordinate systems, such as cylindrical and spherical coordinates, the Laplacian also has a useful form. Informally, the Laplacian Δ f (p) of a function f at a point p measures by how much the average value of f over small spheres or balls centered at p deviates from f (p) .$

In mathematics, the uniformization theorem says that every simply connected Riemann surface is conformally equivalent to one of three Riemann surfaces: the open unit disk, the complex plane, or the Riemann sphere. The theorem is a generalization of the Riemann mapping theorem from simply connected open subsets of the plane to arbitrary simply connected Riemann surfaces.

Shing-Tung Yau is a Chinese-American mathematician and the William Caspar Graustein Professor of Mathematics at Harvard University. In April 2022, Yau announced retirement from Harvard to become Chair Professor of mathematics at Tsinghua University.

In mathematics, two linear operators are called isospectral or cospectral if they have the same spectrum. Roughly speaking, they are supposed to have the same sets of eigenvalues, when those are counted with multiplicity.

In mathematics, spectral graph theory is the study of the properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated with the graph, such as its adjacency matrix or Laplacian matrix.

In mathematics, a CR manifold, or Cauchy–Riemann manifold, is a differentiable manifold together with a geometric structure modeled on that of a real hypersurface in a complex vector space, or more generally modeled on an edge of a wedge.

In the mathematical study of heat conduction and diffusion, a heat kernel is the fundamental solution to the heat equation on a specified domain with appropriate boundary conditions. It is also one of the main tools in the study of the spectrum of the Laplace operator, and is thus of some auxiliary importance throughout mathematical physics. The heat kernel represents the evolution of temperature in a region whose boundary is held fixed at a particular temperature, such that an initial unit of heat energy is placed at a point at time t = 0.

The Minakshisundaram–Pleijel zeta function is a zeta function encoding the eigenvalues of the Laplacian of a compact Riemannian manifold. It was introduced by Subbaramiah Minakshisundaram and Åke Pleijel (1949). The case of a compact region of the plane was treated earlier by Torsten Carleman (1935).

In mathematics, Reidemeister torsion is a topological invariant of manifolds introduced by Kurt Reidemeister for 3-manifolds and generalized to higher dimensions by Wolfgang Franz (1935) and Georges de Rham (1936). Analytic torsion is an invariant of Riemannian manifolds defined by Daniel B. Ray and Isadore M. Singer as an analytic analogue of Reidemeister torsion. Jeff Cheeger and Werner Müller (1978) proved Ray and Singer's conjecture that Reidemeister torsion and analytic torsion are the same for compact Riemannian manifolds.

Spectral geometry is a field in mathematics which concerns relationships between geometric structures of manifolds and spectra of canonically defined differential operators. The case of the Laplace–Beltrami operator on a closed Riemannian manifold has been most intensively studied, although other Laplace operators in differential geometry have also been examined. The field concerns itself with two kinds of questions: direct problems and inverse problems.

<span class="mw-page-title-main">Toshikazu Sunada</span> Japanese mathematician (born 1948)

Toshikazu Sunada is a Japanese mathematician and author of many books and essays on mathematics and mathematical sciences. He is professor emeritus of both Meiji University and Tohoku University. He is also distinguished professor of emeritus at Meiji in recognition of achievement over the course of an academic career. Before he joined Meiji University in 2003, he was professor of mathematics at Nagoya University (1988–1991), at the University of Tokyo (1991–1993), and at Tohoku University (1993–2003). Sunada was involved in the creation of the School of Interdisciplinary Mathematical Sciences at Meiji University and is its first dean (2013–2017). Since 2019, he is President of Mathematics Education Society of Japan.

In mathematics, the Dirichlet eigenvalues are the fundamental modes of vibration of an idealized drum with a given shape. The problem of whether one can hear the shape of a drum is: given the Dirichlet eigenvalues, what features of the shape of the drum can one deduce. Here a "drum" is thought of as an elastic membrane Ω, which is represented as a planar domain whose boundary is fixed. The Dirichlet eigenvalues are found by solving the following problem for an unknown function u ≠ 0 and eigenvalue λ

In Riemannian geometry, Cheng's eigenvalue comparison theorem states in general terms that when a domain is large, the first Dirichlet eigenvalue of its Laplace–Beltrami operator is small. This general characterization is not precise, in part because the notion of "size" of the domain must also account for its curvature. The theorem is due to Cheng (1975b) by Shiu-Yuen Cheng. Using geodesic balls, it can be generalized to certain tubular domains.

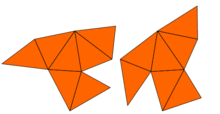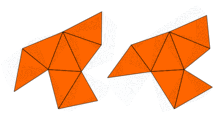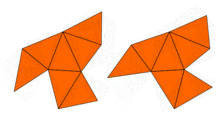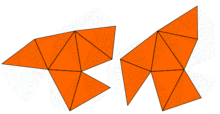
Carolyn S. Gordon is a mathematician and Benjamin Cheney Professor of Mathematics at Dartmouth College. She is most well known for giving a negative answer to the question "Can you hear the shape of a drum?" in her work with David Webb and Scott A. Wolpert. She is a Chauvenet Prize winner and a 2010 Noether Lecturer.

The zeta function of a mathematical operator $is a function defined as$

In mathematics, a Dirac spectrum, named after Paul Dirac, is the spectrum of eigenvalues of a Dirac operator on a Riemannian manifold with a spin structure. The isospectral problem for the Dirac spectrum asks whether two Riemannian spin manifolds have identical spectra. The Dirac spectrum depends on the spin structure in the sense that there exists a Riemannian manifold with two different spin structures that have different Dirac spectra.

In spectral geometry, the Rayleigh–Faber–Krahn inequality, named after its conjecturer, Lord Rayleigh, and two individuals who independently proved the conjecture, G. Faber and Edgar Krahn, is an inequality concerning the lowest Dirichlet eigenvalue of the Laplace operator on a bounded domain in $, . It states that the first Dirichlet eigenvalue is no less than the corresponding Dirichlet eigenvalue of a Euclidean ball having the same volume. Furthermore, the inequality is rigid in the sense that if the first Dirichlet eigenvalue is equal to that of the corresponding ball, then the domain must actually be a ball. In the case of, the inequality essentially states that among all drums of equal area, the circular drum (uniquely) has the lowest voice.$

In mathematics, especially spectral theory, Weyl's law describes the asymptotic behavior of eigenvalues of the Laplace–Beltrami operator. This description was discovered in 1911 by Hermann Weyl for eigenvalues for the Laplace–Beltrami operator acting on functions that vanish at the boundary of a bounded domain $. In particular, he proved that the number,, of Dirichlet eigenvalues less than or equal to satisfies$

Jürg Peter Buser, known as Peter Buser, is a Swiss mathematician, specializing in differential geometry and global analysis.

References

Abikoff, William (January 1995), "Remembering Lipman Bers" (PDF), Notices of the AMS , 42 (1): 8–18
Brossard, Jean; Carmona, René (1986). "Can one hear the dimension of a fractal?". Comm. Math. Phys. 104 (1): 103–122. Bibcode:1986CMaPh.104..103B. doi:10.1007/BF01210795. S2CID 121173871.
Buser, Peter; Conway, John; Doyle, Peter; Semmler, Klaus-Dieter (1994), "Some planar isospectral domains", International Mathematics Research Notices , 1994 (9): 391–400, doi: 10.1155/S1073792894000437
Chapman, S.J. (1995). "Drums that sound the same". American Mathematical Monthly . 102 (February): 124–138. doi:10.2307/2975346. JSTOR 2975346.
Giraud, Olivier; Thas, Koen (2010). "Hearing shapes of drums – mathematical and physical aspects of isospectrality". Reviews of Modern Physics. 82 (3): 2213–2255. arXiv: 1101.1239 . Bibcode:2010RvMP...82.2213G. doi:10.1103/RevModPhys.82.2213. S2CID 119289493.
Gordon, Carolyn; Webb, David (1996), "You can't hear the shape of a drum", American Scientist , 84 (January–February): 46–55, Bibcode:1996AmSci..84...46G
Gordon, C.; Webb, D.; Wolpert, S. (1992), "Isospectral plane domains and surfaces via Riemannian orbifolds", Inventiones Mathematicae, 110 (1): 1–22, Bibcode:1992InMat.110....1G, doi:10.1007/BF01231320, S2CID 122258115
Ivrii, V. Ja. (1980), "The second term of the spectral asymptotics for a Laplace–Beltrami operator on manifolds with boundary", Funktsional. Anal. I Prilozhen, 14 (2): 25–34, doi:10.1007/BF01086550, S2CID 123935462 (In Russian).
Kac, Mark (April 1966). "Can One Hear the Shape of a Drum?" (PDF). American Mathematical Monthly . 73 (4, part 2): 1–23. doi:10.2307/2313748. JSTOR 2313748.
Lapidus, Michel L. (1991), "Can One Hear the Shape of a Fractal Drum? Partial Resolution of the Weyl-Berry Conjecture", Geometric Analysis and Computer Graphics, Math. Sci. Res. Inst. Publ., vol. 17, New York: Springer, pp. 119–126, doi:10.1007/978-1-4613-9711-3_13, ISBN 978-1-4613-9713-7
Lapidus, Michel L. (1993), "Vibrations of fractal drums, the Riemann hypothesis, waves in fractal media, and the Weyl–Berry conjecture", in B. D. Sleeman; R. J. Jarvis (eds.), Ordinary and Partial Differential Equations, Vol IV, Proc. Twelfth Internat. Conf. (Dundee, Scotland, UK, June 1992), Pitman Research Notes in Math. Series, vol. 289, London: Longman and Technical, pp. 126–209
Lapidus, M. L.; van Frankenhuysen, M. (2000), Fractal Geometry and Number Theory: Complex dimensions of fractal strings and zeros of zeta functions, Boston: Birkhauser. (Revised and enlarged second edition to appear in 2005.)
Lapidus, Michel L.; Pomerance, Carl (1993), "The Riemann zeta-function and the one-dimensional Weyl-Berry conjecture for fractal drums", Proc. London Math. Soc., Series 3, 66 (1): 41–69, CiteSeerX 10.1.1.526.854 , doi:10.1112/plms/s3-66.1.41
Lapidus, Michel L.; Pomerance, Carl (1996), "Counterexamples to the modified Weyl–Berry conjecture on fractal drums", Math. Proc. Cambridge Philos. Soc., 119 (1): 167–178, Bibcode:1996MPCPS.119..167L, doi:10.1017/S0305004100074053, S2CID 33567484
Milnor, John (1964), "Eigenvalues of the Laplace operator on certain manifolds", Proceedings of the National Academy of Sciences of the United States of America, 51 (4): 542ff, Bibcode:1964PNAS...51..542M, doi: 10.1073/pnas.51.4.542 , PMC 300113 , PMID 16591156
Sunada, T. (1985), "Riemannian coverings and isospectral manifolds", Ann. of Math., 2, 121 (1): 169–186, doi:10.2307/1971195, JSTOR 1971195
Zelditch, S. (2000), "Spectral determination of analytic bi-axisymmetric plane domains", Geometric and Functional Analysis, 10 (3): 628–677, arXiv: math/9901005 , doi:10.1007/PL00001633, S2CID 16324240

External links

Simulation showing solutions of the wave equation in two isospectral drums
Isospectral Drums by Toby Driscoll at the University of Delaware
Some planar isospectral domains by Peter Buser, John Horton Conway, Peter Doyle, and Klaus-Dieter Semmler
- 3D rendering of the Buser-Conway-Doyle-Semmler homophonic drums
Drums That Sound Alike by Ivars Peterson at the Mathematical Association of America web site
Weisstein, Eric W. "Isospectral Manifolds". MathWorld .
Benguria, Rafael D. (2001) [1994], "Dirichlet eigenvalue", Encyclopedia of Mathematics , EMS Press

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Crowell_SciAm_2022-1] Crowell, Rachel (2022-06-28). "Mathematicians Are Trying to 'Hear' Shapes—And Reach Higher Dimensions". Scientific American. Retrieved 2022-11-15.

[2] "Can One Hear the Shape of a Drum? | Mathematical Association of America".

[3] Kac, Mark (April 1966). "Can One Hear the Shape of a Drum?" (PDF). American Mathematical Monthly . 73 (4, part 2): 16. doi:10.2307/2313748. JSTOR 2313748.

[FOOTNOTEBuserConwayDoyleSemmler1994-4] Buser et al. 1994.

[5] Arrighetti, W.; Gerosa, G. (2005). Can you hear the fractal dimension of a drum?. pp. 65–75. arXiv: math.SP/0503748 . doi:10.1142/9789812701817_0007. ISBN 978-981-256-368-2. S2CID 119709456.{{cite book}}: |journal= ignored (help)

[1]

[2]

[3]

[4]

[5]