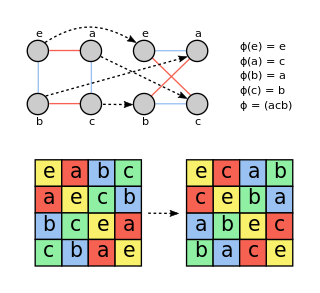
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism group. It is, loosely speaking, the symmetry group of the object.

In mathematics, a diffeomorphism is an isomorphism of differentiable manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are continuously differentiable.

Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's Elements, it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension n, which are called Euclidean n-spaces when one wants to specify their dimension. For n equal to one or two, they are commonly called respectively Euclidean lines and Euclidean planes. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics.

In the mathematical field of representation theory, group representations describe abstract groups in terms of bijective linear transformations of a vector space to itself ; in particular, they can be used to represent group elements as invertible matrices so that the group operation can be represented by matrix multiplication.

In mathematics, many sets of transformations form a group under function composition; for example, the rotations around a point in the plane. It is often useful to consider the group as an abstract group, and to say that one has a group action of the abstract group that consists of performing the transformations of the group of transformations. The reason for distinguishing the group from the transformations is that, generally, a group of transformations of a structure acts also on various related structures; for example, the above rotation group acts also on triangles by transforming triangles into triangles.

In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object X is G = Sym(X).

In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible, with the identity matrix as the identity element of the group. The group is so named because the columns of an invertible matrix are linearly independent, hence the vectors/points they define are in general linear position, and matrices in the general linear group take points in general linear position to points in general linear position.

In mathematics, the orthogonal group in dimension n, denoted O(n), is the group of distance-preserving transformations of a Euclidean space of dimension n that preserve a fixed point, where the group operation is given by composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of n × n orthogonal matrices, where the group operation is given by matrix multiplication (an orthogonal matrix is a real matrix whose inverse equals its transpose). The orthogonal group is an algebraic group and a Lie group. It is compact.
In mathematics, the affine group or general affine group of any affine space is the group of all invertible affine transformations from the space into itself. In the case of a Euclidean space, the affine group consists of those functions from the space to itself such that the image of every line is a line.

In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties related to parallelism and ratio of lengths for parallel line segments. Affine space is the setting for affine geometry.

In mathematics, especially in the group theoretic area of algebra, the projective linear group (also known as the projective general linear group or PGL) is the induced action of the general linear group of a vector space V on the associated projective space P(V). Explicitly, the projective linear group is the quotient group
In mathematics, a generalized flag variety is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real or complex numbers, a generalized flag variety is a smooth or complex manifold, called a real or complexflag manifold. Flag varieties are naturally projective varieties.
The concept of system of imprimitivity is used in mathematics, particularly in algebra and analysis, both within the context of the theory of group representations. It was used by George Mackey as the basis for his theory of induced unitary representations of locally compact groups.
In mathematics, the Stiefel manifold is the set of all orthonormal k-frames in That is, it is the set of ordered orthonormal k-tuples of vectors in It is named after Swiss mathematician Eduard Stiefel. Likewise one can define the complex Stiefel manifold of orthonormal k-frames in and the quaternionic Stiefel manifold of orthonormal k-frames in . More generally, the construction applies to any real, complex, or quaternionic inner product space.

In mathematics, a symmetric space is a Riemannian manifold whose group of symmetries contains an inversion symmetry about every point. This can be studied with the tools of Riemannian geometry, leading to consequences in the theory of holonomy; or algebraically through Lie theory, which allowed Cartan to give a complete classification. Symmetric spaces commonly occur in differential geometry, representation theory and harmonic analysis.
In mathematics, a Gelfand pair is a pair (G,K ) consisting of a group G and a subgroup K (called an Euler subgroup of G) that satisfies a certain property on restricted representations. The theory of Gelfand pairs is closely related to the topic of spherical functions in the classical theory of special functions, and to the theory of Riemannian symmetric spaces in differential geometry. Broadly speaking, the theory exists to abstract from these theories their content in terms of harmonic analysis and representation theory.
In mathematics, the Lagrangian Grassmannian is the smooth manifold of Lagrangian subspaces of a real symplectic vector space V. Its dimension is 1/2n(n + 1) (where the dimension of V is 2n). It may be identified with the homogeneous space
Affine geometry, broadly speaking, is the study of the geometrical properties of lines, planes, and their higher dimensional analogs, in which a notion of "parallel" is retained, but no metrical notions of distance or angle are. Affine spaces differ from linear spaces in that they do not have a distinguished choice of origin. So, in the words of Marcel Berger, "An affine space is nothing more than a vector space whose origin we try to forget about, by adding translations to the linear maps." Accordingly, a complex affine space, that is an affine space over the complex numbers, is like a complex vector space, but without a distinguished point to serve as the origin.

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines should be regarded as circles of infinite radius and that points in the plane should be regarded as circles of zero radius.












