Hyperbolastic functions

Graphic describing the Hyperbolastic Type I function with varying parameter values.

Graphic describing the Hyperbolastic Type I function with varying parameter values.

Graphic describing the Hyperbolastic Type II function with varying parameter values.

Graphic describing the Hyperbolastic Type II function with varying parameter values.

Graphic describing the Hyperbolastic Type III function with varying parameter values.

Graphic describing the Hyperbolastic cumulative distribution function of type III with varying parameter values.

Graphic describing the Hyperbolastic probability density function of type III with varying parameter values.

The hyperbolastic functions, also known as hyperbolastic growth models, are mathematical functions that are used in medical statistical modeling. These models were originally developed to capture the growth dynamics of multicellular tumor spheres, and were introduced in 2005 by Mohammad Tabatabai, David Williams, and Zoran Bursac. ^[1] The precision of hyperbolastic functions in modeling real world problems is somewhat due to their flexibility in their point of inflection. ^{[1] [2]} These functions can be used in a wide variety of modeling problems such as tumor growth, stem cell proliferation, pharma kinetics, cancer growth, sigmoid activation function in neural networks, and epidemiological disease progression or regression. ^{[1] [3] [4]}

The hyperbolastic functions can model both growth and decay curves until it reaches carrying capacity. Due to their flexibility, these models have diverse applications in the medical field, with the ability to capture disease progression with an intervening treatment. As the figures indicate, hyperbolastic functions can fit a sigmoidal curve indicating that the slowest rate occurs at the early and late stages. ^[5] In addition to the presenting sigmoidal shapes, it can also accommodate biphasic situations where medical interventions slow or reverse disease progression; but, when the effect of the treatment vanishes, the disease will begin the second phase of its progression until it reaches its horizontal asymptote.

One of the main characteristics these functions have is that they cannot only fit sigmoidal shapes, but can also model biphasic growth patterns that other classical sigmoidal curves cannot adequately model. This distinguishing feature has advantageous applications in various fields including medicine, biology, economics, engineering, agronomy, and computer aided system theory. ^{[6] [7] [8] [9] [10]}

Function H1

The hyperbolastic rate equation of type I, denoted H1, is given by

$${\displaystyle {\frac {dP(x)}{dx}}={\frac {P(x)}{M}}\left(M-P\left(x\right)\right)\left(\delta +{\frac {\theta }{\sqrt {1+x^{2}}}}\right),}$$

where ${\displaystyle x}$ is any real number and ${\displaystyle P\left(x\right)}$ is the population size at ${\displaystyle x}$. The parameter ${\displaystyle M}$ represents carrying capacity, and parameters ${\displaystyle \delta }$ and ${\displaystyle \theta }$ jointly represent growth rate. The parameter ${\displaystyle \theta }$ gives the distance from a symmetric sigmoidal curve. Solving the hyperbolastic rate equation of type I for ${\displaystyle P\left(x\right)}$ gives

$${\displaystyle P(x)={\frac {M}{1+\alpha e^{-\delta x-\theta \operatorname {arsinh} (x)}}},}$$

where ${\displaystyle \operatorname {arsinh} }$ is the inverse hyperbolic sine function. If one desires to use the initial condition ${\displaystyle P\left(x_{0}\right)=P_{0}}$, then ${\displaystyle \alpha }$ can be expressed as

${\displaystyle \alpha ={\frac {M-P_{0}}{P_{0}}}e^{\delta x_{0}+\theta \operatorname {arsinh} (x_{0})}}$.

If ${\displaystyle x_{0}=0}$, then ${\displaystyle \alpha }$ reduces to

${\displaystyle \alpha ={\frac {M-P_{0}}{P_{0}}}}$.

The hyperbolastic function of type I generalizes the logistic function. If the parameters ${\displaystyle \theta =0}$, then it would become a logistic function. This function ${\displaystyle P(x)}$ is a hyperbolastic function of type I. The standard hyperbolastic function of type I is

${\displaystyle P(x)={\frac {1}{1+e^{-x-\theta \operatorname {arsinh} (x)}}}}$.

Function H2

The hyperbolastic rate equation of type II, denoted by H2, is defined as

${\displaystyle {\frac {dP(x)}{dx}}={\frac {\alpha \delta \gamma P^{2}(x)x^{\gamma -1}}{M}}\tanh \left({\frac {M-P(x)}{\alpha P(x)}}\right),}$

where ${\displaystyle \tanh }$ is the hyperbolic tangent function, ${\displaystyle M}$ is the carrying capacity, and both ${\displaystyle \delta }$ and ${\displaystyle \gamma >0}$ jointly determine the growth rate. In addition, the parameter ${\displaystyle \gamma }$ represents acceleration in the time course. Solving the hyperbolastic rate function of type II for ${\displaystyle P\left(x\right)}$ gives

${\displaystyle P(x)={\frac {M}{1+\alpha \operatorname {arsinh} \left(e^{-\delta x^{\gamma }}\right)}}}$.

If one desires to use initial condition ${\displaystyle P(x_{0})=P_{0},}$ then ${\displaystyle \alpha }$ can be expressed as

${\displaystyle \alpha ={\frac {M-P_{0}}{P_{0}\operatorname {arsinh} \left(e^{-\delta x_{0}^{\gamma }}\right)}}}$.

If ${\displaystyle x_{0}=0}$, then ${\displaystyle \alpha }$ reduces to

${\displaystyle \alpha ={\frac {M-P_{0}}{P_{0}\operatorname {arsinh} (1)}}}$.

The standard hyperbolastic function of type II is defined as

${\displaystyle P(x)={\frac {1}{1+\operatorname {arsinh} \left(e^{-x}\right)}}}$.

Function H3

The hyperbolastic rate equation of type III is denoted by H3 and has the form

${\displaystyle {\frac {dP(t)}{dt}}=\left(M-P\left(t\right)\right)\left(\delta \gamma t^{\gamma -1}+{\frac {\theta }{\sqrt {1+\theta ^{2}t^{2}}}}\right)}$,

where ${\displaystyle t}$ > 0. The parameter ${\displaystyle M}$ represents the carrying capacity, and the parameters ${\displaystyle \delta ,}$${\displaystyle \gamma ,}$ and ${\displaystyle \theta }$ jointly determine the growth rate. The parameter ${\displaystyle \gamma ,}$ represents acceleration of the time scale, while the size of ${\displaystyle \theta }$ represents distance from a symmetric sigmoidal curve. The solution to the differential equation of type III is

${\displaystyle P(t)=M-\alpha e^{-\delta t^{\gamma }-\operatorname {arsinh} (\theta t)}}$,

with the initial condition ${\displaystyle P\left(t_{0}\right)=P_{0}}$ we can express ${\displaystyle \alpha }$ as

${\displaystyle \alpha =\left(M-P_{0}\right)e^{\delta t_{0}^{\gamma }+\operatorname {arsinh} (\theta t_{0})}}$.

The hyperbolastic distribution of type III is a three-parameter family of continuous probability distributions with scale parameters ${\displaystyle \delta }$ > 0, and ${\displaystyle \theta }$ ≥ 0 and parameter ${\displaystyle \gamma }$ as the shape parameter. When the parameter ${\displaystyle \theta }$ = 0, the hyperbolastic distribution of type III is reduced to the weibull distribution. ^[11] The hyperbolastic cumulative distribution function of type III is given by

${\displaystyle F(x;\delta ,\gamma ,\theta )={\begin{cases}1-e^{-\delta x^{\gamma }-\operatorname {arsinh} (\theta x)}&x\geq 0,\\0&x<0\end{cases}}}$,

and its corresponding probability density function is

${\displaystyle f(x;\delta ,\gamma ,\theta )={\begin{cases}e^{-\delta x^{\gamma }-\operatorname {arsinh} (\theta x)}\left(\delta \gamma x^{\gamma -1}+{\frac {\theta }{\sqrt {1+\theta ^{2}x^{2}}}}\right)&x\geq 0,\\0&x<0\end{cases}}}$.

The hazard function ${\displaystyle h}$ (or failure rate) is given by

${\displaystyle h\left(x;\delta ,\gamma ,\theta \right)=\delta \gamma x^{\gamma -1}+{\frac {\theta }{\sqrt {1+x^{2}\theta ^{2}}}}.}$

The survival function ${\displaystyle S}$ is given by

${\displaystyle S(x;\delta ,\gamma ,\theta )=e^{-\delta x^{\gamma }-\operatorname {arsinh} (\theta x)}.}$

The standard hyperbolastic cumulative distribution function of type III is defined as

${\displaystyle F\left(x\right)=1-e^{-x-\operatorname {arsinh} (x)}}$,

and its corresponding probability density function is

${\displaystyle f(x)=e^{-x-\operatorname {arsinh} (x)}\left(1+{\frac {1}{\sqrt {1+x^{2}}}}\right)}$.

Properties

If one desires to calculate the point ${\displaystyle x}$ where the population reaches a percentage of its carrying capacity ${\displaystyle M}$, then one can solve the equation

${\displaystyle P(x)=kM}$

for ${\displaystyle x}$, where ${\displaystyle 0<k<1}$. For instance, the half point can be found by setting ${\displaystyle k={\frac {1}{2}}}$.

Applications

3D Hyperbolastic graph of phytoplankton biomass as a function of nutrient concentration and time

According to stem cell researchers at McGowan Institute for Regenerative Medicine at the University of Pittsburgh, "a newer model [called the hyperbolastic type III or] H3 is a differential equation that also describes the cell growth. This model allows for much more variation and has been proven to better predict growth." ^[12]

The hyperbolastic growth models H1, H2, and H3 have been applied to analyze the growth of solid Ehrlich carcinoma using a variety of treatments. ^[13]

In animal science, ^[14] the hyperbolastic functions have been used for modeling broiler chicken growth. ^{[15] [16]} The hyperbolastic model of type III was used to determine the size of the recovering wound. ^[17]

In the area of wound healing, the hyperbolastic models accurately representing the time course of healing. Such functions have been used to investigate variations in the healing velocity among different kinds of wounds and at different stages in the healing process taking into consideration the areas of trace elements, growth factors, diabetic wounds, and nutrition. ^{[18] [19]}

Another application of hyperbolastic functions is in the area of the stochastic diffusion process, ^[20] whose mean function is a hyperbolastic curve. The main characteristics of the process are studied and the maximum likelihood estimation for the parameters of the process is considered. ^[21] To this end, the firefly metaheuristic optimization algorithm is applied after bounding the parametric space by a stage wise procedure. Some examples based on simulated sample paths and real data illustrate this development. A sample path of a diffusion process models the trajectory of a particle embedded in a flowing fluid and subjected to random displacements due to collisions with other particles, which is called Brownian motion. ^{[22] [23] [24] [25] [26]} The hyperbolastic function of type III was used to model the proliferation of both adult mesenchymal and embryonic stem cells; ^{[27] [28] [29] [30]} and, the hyperbolastic mixed model of type II has been used in modeling cervical cancer data. ^[31] Hyperbolastic curves can be an important tool in analyzing cellular growth, the fitting of biological curves, the growth of phytoplankton, and instantaneous maturity rate. ^{[32] [33] [34] [35]}

In forest ecology and management, the hyperbolastic models have been applied to model the relationship between DBH and height. ^[36]

The multivariable hyperbolastic model type III has been used to analyze the growth dynamics of phytoplankton taking into consideration the concentration of nutrients. ^[37]

Hyperbolastic regressions

Cumulative Distribution Function of Hyperbolastic Type I, Logistic, and Hyperbolastic Type II

PDF of H1, Logistic, and H2

Hyperbolastic regressions are statistical models that utilize standard hyperbolastic functions to model a dichotomous or multinomial outcome variable. The purpose of hyperbolastic regression is to predict an outcome using a set of explanatory (independent) variables. These types of regressions are routinely used in many areas including medical, public health, dental, biomedical, as well as social, behavioral, and engineering sciences. For instance, binary regression analysis has been used to predict endoscopic lesions in iron deficiency anemia. ^[38] In addition, binary regression was applied to differentiate between malignant and benign adnexal mass prior to surgery. ^[39]

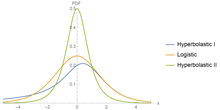
The binary hyperbolastic regression of type I

Let ${\displaystyle Y}$ be a binary outcome variable which can assume one of two mutually exclusive values, success or failure. If we code success as ${\displaystyle Y=1}$ and failure as ${\displaystyle Y=0}$, then for parameter ${\displaystyle \theta \geq -1}$, the hyperbolastic success probability of type I with a sample of size ${\displaystyle n}$ as a function of parameter ${\displaystyle \theta }$ and parameter vector ${\displaystyle {\boldsymbol {\beta }}=(\beta _{0},\beta _{1},\ldots ,\beta _{p})}$ given a ${\displaystyle p}$-dimensional vector of explanatory variables is defined as ${\displaystyle \mathbf {x} _{i}=(x_{i1},\ x_{i2},\ldots ,\ x_{ip})^{T}}$, where ${\displaystyle i=1,2,\ldots ,n}$, is given by

${\displaystyle \pi (\mathbf {x} _{i};{\boldsymbol {\beta }})=P(y_{i}=1|\mathbf {x} _{i};{\boldsymbol {\beta }})={\frac {1}{1+e^{-(\beta _{0}+\sum _{s=1}^{p}{\beta _{s}x_{is}})-\theta \operatorname {arsinh} (\beta _{0}+\sum _{s=1}^{p}{\beta _{s}x_{is}})}}}}$.

The odds of success is the ratio of the probability of success to the probability of failure. For binary hyperbolastic regression of type I, the odds of success is denoted by ${\displaystyle Odds_{H1}}$ and expressed by the equation

${\displaystyle Odds_{H1}=e^{\beta _{0}+\sum _{s=1}^{p}{\beta _{s}x_{is}}+\theta \operatorname {arsinh} (\beta _{0}+\sum _{s=1}^{p}{\beta _{s}x_{is}})}}$.

The logarithm of ${\displaystyle Odds_{H1}}$ is called the logit of binary hyperbolastic regression of type I. The logit transformation is denoted by ${\displaystyle L_{H1}}$ and can be written as

${\displaystyle L_{H1}=\beta _{0}+\sum _{s=1}^{p}{\beta _{s}x_{is}}+\theta \operatorname {arsinh} [\beta _{0}+\sum _{s=1}^{p}{\beta _{s}x_{is}}]}$.

Shannon information for binary hyperbolastic of type I (H1)

The Shannon information for the random variable ${\displaystyle Y}$ is defined as

${\displaystyle I(y)=-{log}_{b}P(y)}$

where the base of logarithm ${\displaystyle b>0}$ and ${\displaystyle b\neq 1}$. For binary outcome, ${\displaystyle b}$ is equal to ${\displaystyle 2}$.

For the binary hyperbolastic regression of type I, the information ${\displaystyle I(y)}$ is given by

${\displaystyle I(y)={\begin{cases}-log_{b}{\frac {1}{1+e^{-Z-\theta \operatorname {arsinh} (Z)}}}&y=1,\\-log_{b}{\frac {e^{-Z-\theta \operatorname {arsinh} (Z)}}{1+e^{-Z-\theta \operatorname {arsinh} (Z)}}}&y=0\end{cases}}}$,

where ${\displaystyle Z=\beta _{0}+\sum _{s=1}^{p}\beta _{s}x_{s}}$, and ${\displaystyle x_{s}}$ is the ${\displaystyle s^{th}}$ input data. For a random sample of binary outcomes of size ${\displaystyle n}$, the average empirical information for hyperbolastic H1 can be estimated by

${\displaystyle {\overline {I(y)}}={\begin{cases}-{\frac {1}{n}}\sum _{i=1}^{n}{log_{b}{\frac {1}{1+e^{-Z_{i}-\theta \operatorname {arsinh} (Z_{i})}}}}&y=1,\\-{\frac {1}{n}}\sum _{i=1}^{n}{log_{b}{\frac {e^{-Z_{i}-\theta \operatorname {arsinh} (Z_{i})}}{1+e^{-Z_{i}-\theta \operatorname {arsinh} (Z_{i})}}}}&y=0\end{cases}}}$,

where ${\displaystyle Z_{i}=\beta _{0}+\sum _{s=1}^{p}\beta _{s}x_{is}}$, and ${\displaystyle x_{is}}$ is the ${\displaystyle s^{th}}$ input data for the ${\displaystyle i^{th}}$ observation.

Information Entropy for hyperbolastic H1

Information entropy measures the loss of information in a transmitted message or signal. In machine learning applications, it is the number of bits necessary to transmit a randomly selected event from a probability distribution. For a discrete random variable ${\displaystyle Y}$, the information entropy ${\displaystyle H}$ is defined as

${\displaystyle H=-\sum _{y\in Y}{P(y)\ {log}_{b}P(y)}}$

where ${\displaystyle P(y)}$ is the probability mass function for the random variable ${\displaystyle Y}$.

The information entropy is the mathematical expectation of ${\displaystyle I(y)}$ with respect to probability mass function ${\displaystyle P(y)}$. The Information entropy has many applications in machine learning and artificial intelligence such as classification modeling and decision trees. For the hyperbolastic H1, the entropy ${\displaystyle H}$ is equal to

${\displaystyle {\begin{aligned}H&=-\sum _{y\in \{0,1\}}{P(Y=y;\mathbf {x} ,{\boldsymbol {\beta }})log_{b}(P(Y=y;\mathbf {x} ,{\boldsymbol {\beta }}))}\\&=-[\pi (\mathbf {x}$ ;{\boldsymbol {\beta }})\ log_{b}(\pi (\mathbf {x} ;{\boldsymbol {\beta }})+(1-\pi (\mathbf {x} ;{\boldsymbol {\beta }}))log_{b}(1-\pi (\mathbf {x} ;{\boldsymbol {\beta }}))]\\&={log}_{b}(1+e^{-Z-\theta \operatorname {arsinh} (Z)})-{\frac {e^{-Z-\theta \operatorname {arsinh} (Z)}{log}_{b}(e^{-Z-\theta \operatorname {arsinh} (Z)})}{1+e^{-Z-\theta \operatorname {arsinh} (Z)}}}\end{aligned}}}

The estimated average entropy for hyperbolastic H1 is denoted by ${\displaystyle {\bar {H}}}$ and is given by

${\displaystyle {\bar {H}}={\frac {1}{n}}\sum _{i=1}^{n}{[log_{b}(1+e^{{-Z}_{i}-\theta \operatorname {arsinh} (Z_{i})})-}{\frac {e^{{-Z}_{i}-\theta \operatorname {arsinh} (Z_{i})}\ {log}_{b}(e^{{-Z}_{i}-\theta \operatorname {arsinh} ((Z_{i})})}{1+e^{{-Z}_{i}-\theta \operatorname {arsinh} (Z_{i})}}}]}$

Binary Cross-entropy for hyperbolastic H1

The binary cross-entropy compares the observed ${\displaystyle y\in \{0,1\}}$ with the predicted probabilities. The average binary cross-entropy for hyperbolastic H1 is denoted by ${\displaystyle {\overline {C}}}$ and is equal to

${\displaystyle {\begin{aligned}{\overline {C}}&=-{\frac {1}{n}}\sum _{i=1}^{n}{{[y}_{i}log_{b}(\pi (x_{i};{\boldsymbol {\beta }}))+}{(1-y}_{i})log_{b}(1-\pi (x_{i};{\boldsymbol {\beta }}))]\\&={\frac {1}{n}}\sum _{i=1}^{n}{[log_{b}(1+e^{{-Z}_{i}-\theta \operatorname {arsinh} (Z_{i})})-}{(1-y}_{i})log_{b}(e^{{-Z}_{i}-\theta \operatorname {arsinh} (Z_{i})})]\end{aligned}}}$

The binary hyperbolastic regression of type II

The hyperbolastic regression of type II is an alternative method for the analysis of binary data with robust properties. For the binary outcome variable ${\displaystyle Y}$, the hyperbolastic success probability of type II is a function of a ${\displaystyle p}$-dimensional vector of explanatory variables ${\displaystyle \mathbf {x} _{i}}$ given by

${\displaystyle \pi (\mathbf {x} _{i};{\boldsymbol {\beta }})=P(y_{i}=1|\mathbf {x} _{i};{\boldsymbol {\beta }})={\frac {1}{1+\operatorname {arsinh} [e^{-(\beta _{0}+\sum _{s=1}^{p}{\beta _{s}x_{is}})}]}}}$ ,

For the binary hyperbolastic regression of type II, the odds of success is denoted by ${\displaystyle Odds_{H2}}$ and is defined as

${\displaystyle Odds_{H2}={\frac {1}{\operatorname {arsinh} [e^{-(\beta _{0}+\sum _{s=1}^{p}{\beta _{s}x_{is}})}]}}.}$

The logit transformation ${\displaystyle L_{H2}}$ is given by

${\displaystyle L_{H2}=-\log {(\operatorname {arsinh} [e^{-(\beta _{0}+\sum _{s=1}^{p}{\beta _{s}x_{is}})}])}}$

Shannon information for binary hyperbolastic of type II (H2)

For the binary hyperbolastic regression H2, the Shannon information ${\displaystyle I(y)}$ is given by

${\displaystyle I(y)={\begin{cases}-log_{b}{\frac {1}{1+arsinh(e^{-Z})}}&y=1\\-log_{b}{\frac {arsinh(e^{-Z})}{1+arsinh(e^{-Z})}}&y=0\end{cases}}}$

where ${\displaystyle Z=\beta _{0}+\sum _{s=1}^{p}\beta _{s}x_{s}}$, and ${\displaystyle x_{s}}$ is the ${\displaystyle s^{th}}$ input data. For a random sample of binary outcomes of size ${\displaystyle n}$, the average empirical information for hyperbolastic H2 is estimated by

${\displaystyle {\overline {I(y)}}={\begin{cases}-{\frac {1}{n}}\sum _{i=1}^{n}log_{b}{\frac {1}{1+arsinh(e^{-Z_{i}})}}&y=1\\-{\frac {1}{n}}\sum _{i=1}^{n}log_{b}{\frac {arsinh(e^{-Z_{i}})}{1+arsinh(e^{-Z_{i}})}}&y=0\end{cases}}}$

where ${\displaystyle Z_{i}=\beta _{0}+\sum _{s=1}^{p}\beta _{s}x_{is}}$, and ${\displaystyle x_{is}}$ is the ${\displaystyle s^{th}}$ input data for the ${\displaystyle i^{th}}$ observation.

Information Entropy for hyperbolastic H2

For the hyperbolastic H2, the information entropy ${\displaystyle H}$ is equal to

${\displaystyle {\begin{aligned}H&=-\sum _{y\in \{0,1\}}{P(Y=y;\mathbf {x} ,{\boldsymbol {\beta }})log_{b}(P(Y=y;\mathbf {x} ,{\boldsymbol {\beta }}))}\\&=-[\pi (\mathbf {x}$ ;{\boldsymbol {\beta }})\ log_{b}(\pi (\mathbf {x} ;{\boldsymbol {\beta }}))+(1-\pi (\mathbf {x} ;{\boldsymbol {\beta }}))log_{b}(1-\pi (\mathbf {x} ;{\boldsymbol {\beta }}))]\\&=log_{b}(1+arsinh(e^{-Z}))-{\frac {arsinh(e^{-Z})log_{b}(arsinh(e^{-Z}))}{1+arsinh(e^{-Z})}}\end{aligned}}}

and the estimated average entropy ${\displaystyle {\bar {H}}}$ for hyperbolastic H2 is

${\displaystyle {\bar {H}}={\frac {1}{n}}\sum _{i=1}^{n}{[log_{b}(1+{arsinh(e}^{{-Z}_{i}}))-}{\frac {{arsinh(e}^{{-Z}_{i}})\ {log}_{b}{(arsinh(e}^{{-Z}_{i}}))}{1+{arsinh(e}^{{-Z}_{i}})}}]}$

Binary Cross-entropy for hyperbolastic H2

The average binary cross-entropy ${\displaystyle {\overline {C}}}$ for hyperbolastic H2 is

${\displaystyle {\begin{aligned}{\overline {C}}&=-{\frac {1}{n}}\sum _{i=1}^{n}{{[y}_{i}log_{b}(\pi (x_{i};\beta ))+}{(1-y}_{i})log_{b}(1-\pi (x_{i};\beta ))]\\&={\frac {1}{n}}\sum _{i=1}^{n}{[log_{b}(1+{arsinh(e}^{{-Z}_{i}}))-}{(1-y}_{i})log_{b}({arsinh(e}^{{-Z}_{i}}))]\end{aligned}}}$

Parameter estimation for the binary hyperbolastic regression of type I and II

The estimate of the parameter vector ${\displaystyle {\boldsymbol {\beta }}}$ can be obtained by maximizing the log-likelihood function

${\displaystyle {\hat {\beta }}={\underset {\boldsymbol {\beta }}{\operatorname {argmax} }}{\sum _{i=1}^{n}[y_{i}ln(\pi (\mathbf {x} _{i};{\boldsymbol {\beta }}))+(1-y_{i})ln(1-\pi (\mathbf {x} _{i};{\boldsymbol {\beta }}))]}}$

where ${\displaystyle \pi (\mathbf {x} _{i};{\boldsymbol {\beta }})}$ is defined according to one of the two types of hyberbolastic functions used.

The multinomial hyperbolastic regression of type I and II

The generalization of the binary hyperbolastic regression to multinomial hyperbolastic regression has a response variable ${\displaystyle y_{i}}$ for individual ${\displaystyle i}$ with ${\displaystyle k}$ categories (i.e. ${\displaystyle y_{i}\in \{1,2,\ldots ,k\}}$). When ${\displaystyle k=2}$, this model reduces to a binary hyperbolastic regression. For each ${\displaystyle i=1,2,\ldots ,n}$, we form ${\displaystyle k}$ indicator variables ${\displaystyle y_{ij}}$ where

${\displaystyle y_{ij}={\begin{cases}1&{\text{if }}y_{i}=j,\\0&{\text{if }}y_{i}\neq j\end{cases}}}$,

meaning that ${\displaystyle y_{ij}=1}$ whenever the ${\displaystyle i^{th}}$ response is in category ${\displaystyle j}$ and ${\displaystyle 0}$ otherwise.

Define parameter vector ${\displaystyle {\boldsymbol {\beta }}_{j}=(\beta _{j0},\beta _{j1},\ldots ,\beta _{jp})}$ in a ${\displaystyle p+1}$-dimensional Euclidean space and ${\displaystyle {\boldsymbol {\beta }}=({\boldsymbol {\beta }}_{1},\ldots ,{\boldsymbol {\beta }}_{k-1})^{T}}$.

Using category 1 as a reference and ${\displaystyle \pi _{1}(\mathbf {x} _{i};{\boldsymbol {\beta }})}$ as its corresponding probability function, the multinomial hyperbolastic regression of type I probabilities are defined as

${\displaystyle \pi _{1}(\mathbf {x} _{i};{\boldsymbol {\beta }})=P(y_{i}=1|\mathbf {x} _{i};{\boldsymbol {\beta }})={\frac {1}{1+\sum _{s=2}^{k}e^{-\eta _{s}(\mathbf {x} _{i};{\boldsymbol {\beta }})-\theta \operatorname {arsinh} [\eta _{s}(\mathbf {x} _{i};{\boldsymbol {\beta }})]}}}}$

and for ${\displaystyle j=2,\ldots ,k}$,

${\displaystyle \pi _{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})=P(y_{i}=j|\mathbf {x} _{i};{\boldsymbol {\beta }})={\frac {e^{-\eta _{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})-\theta \operatorname {arsinh} [\eta _{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})]}}{1+\sum _{s=2}^{k}e^{-\eta _{s}(\mathbf {x} _{i};{\boldsymbol {\beta }})-\theta \operatorname {arsinh} [\eta _{s}(\mathbf {x} _{i};{\boldsymbol {\beta }})]}}}}$

Similarly, for the multinomial hyperbolastic regression of type II we have

${\displaystyle \pi _{1}(\mathbf {x} _{i};{\boldsymbol {\beta }})=P(y_{i}=1|\mathbf {x} _{i};{\boldsymbol {\beta }})={\frac {1}{1+\sum _{s=2}^{k}arsinh[e^{-\eta _{s}(\mathbf {x} _{i};{\boldsymbol {\beta }})}]}}}$

and for ${\displaystyle j=2,\ldots ,k}$,

${\displaystyle \pi _{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})=P(y_{i}=j|\mathbf {x} _{i};{\boldsymbol {\beta }})={\frac {arsinh[e^{-\eta _{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})}]}{1+\sum _{s=2}^{k}arsinh[e^{-\eta _{s}(\mathbf {x} _{i};{\boldsymbol {\beta }})}]}}}$

where ${\displaystyle \eta _{s}(\mathbf {x} _{i};{\boldsymbol {\beta }})=\beta _{s0}+\sum _{l=1}^{p}\beta _{sl}x_{il}}$ with ${\displaystyle s=2,\dots ,k}$ and ${\displaystyle i=1,\dots ,n}$.

The choice of ${\displaystyle \pi _{i}(\mathbf {x_{i}}$ ;{\boldsymbol {\beta }})} is dependent on the choice of hyperbolastic H1 or H2.

Shannon Information for multiclass hyperbolastic H1 or H2

For the multiclass ${\displaystyle (j=1,2,\dots ,k)}$, the Shannon information ${\displaystyle I_{j}}$ is

${\displaystyle I_{j}=-log_{b}(\pi _{j}(\mathbf {x}$ ;{\boldsymbol {\beta }}))}.

For a random sample of size ${\displaystyle n}$, the empirical multiclass information can be estimated by

${\displaystyle {\overline {I_{j}}}=-{\frac {1}{n}}\sum _{i=1}^{n}{log_{b}(\pi _{j}(\mathbf {x_{i}}$ ;{\boldsymbol {\beta }}))}}.

Multiclass Entropy in Information Theory

For a discrete random variable ${\displaystyle Y}$, the multiclass information entropy is defined as

${\displaystyle H=-\sum _{y\in Y}{P(y)\ {log}_{b}P(y)}}$

where ${\displaystyle P(y)}$ is the probability mass function for the multiclass random variable ${\displaystyle Y}$.

For the hyperbolastic H1 or H2, the multiclass entropy ${\displaystyle H}$ is equal to

${\displaystyle H=-\sum _{j=1}^{k}{[\pi _{j}(\mathbf {x}$ ;{\boldsymbol {\beta }})log_{b}(\pi _{j}(\mathbf {x} ;{\boldsymbol {\beta }}))]}}

The estimated average multiclass entropy ${\displaystyle {\overline {H}}}$ is equal to

${\displaystyle {\overline {H}}=-{\frac {1}{n}}\sum _{i=1}^{n}{\sum _{j=1}^{k}{[\pi _{j}(\mathbf {x_{i}}$ ;{\boldsymbol {\beta }})log_{b}(\pi _{j}(\mathbf {x_{i}} ;{\boldsymbol {\beta }}))]}}}

Multiclass Cross-entropy for hyperbolastic H1 or H2

Multiclass cross-entropy compares the observed multiclass output with the predicted probabilities. For a random sample of multiclass outcomes of size ${\displaystyle n}$, the average multiclass cross-entropy ${\displaystyle {\overline {C}}}$ for hyperbolastic H1 or H2 can be estimated by

${\displaystyle {\overline {C}}=-{\frac {1}{n}}\sum _{i=1}^{n}{\sum _{j=1}^{k}{[y_{ij}log_{b}(\pi _{j}(\mathbf {x_{i}}$ ;{\boldsymbol {\beta }}))]}}}

The log-odds of membership in category ${\displaystyle j}$ versus the reference category 1, denoted by ${\displaystyle o_{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})}$, is equal to

${\displaystyle o_{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})=ln[{\frac {\pi _{j}(\mathbf {x} _{i};{\boldsymbol {\beta }})}{\pi _{1}(\mathbf {x} _{i};{\boldsymbol {\beta }})}}]}$

where ${\displaystyle j=2,\ldots ,k}$ and ${\displaystyle i=1,\ldots ,n}$. The estimated parameter matrix ${\displaystyle {\hat {\boldsymbol {\beta }}}}$ of multinomial hyperbolastic regression is obtained by maximizing the log-likelihood function. The maximum likelihood estimates of the parameter matrix ${\displaystyle {\boldsymbol {\beta }}}$ is

${\displaystyle {\boldsymbol {\hat {\beta }}}={\underset {\boldsymbol {\beta }}{\operatorname {argmax} }}{\sum _{i=1}^{n}(y_{i1}ln[\pi _{1}(\mathbf {x} _{i};{\boldsymbol {\beta }})]+y_{i2}ln[\pi _{2}(\mathbf {x} _{i};{\boldsymbol {\beta }})]+\ldots +y_{ik}ln[\pi _{k}(\mathbf {x} _{i};{\boldsymbol {\beta }})])}}$

References

1. Tabatabai, Mohammad; Williams, David; Bursac, Zoran (2005). "Hyperbolastic growth models: Theory and application". Theoretical Biology and Medical Modelling. 2: 14. doi: 10.1186/1742-4682-2-14 . PMC   1084364 . PMID   15799781.
2. Himali, L.P.; Xia, Zhiming (2022). "Performance of the Survival models in Socioeconomic Phenomena". Vavuniya Journal of Science. 1 (2): 9–19. ISSN   2950-7154.
3. Acton, Q. Ashton (2012). Blood Cells—Advances in Research and Application: 2012 Edition. ScholarlyEditions. ISBN   978-1-4649-9316-9.^{[ page needed ]}
4. Wadkin, L. E.; Orozco-Fuentes, S.; Neganova, I.; Lako, M.; Parker, N. G.; Shukurov, A. (2020). "An introduction to the mathematical modelling of iPSCs". Recent Advances in IPSC Technology. 5. arXiv: 2010.15493 .
5. Albano, G.; Giorno, V.; Roman-Roman, P.; Torres-Ruiz, F. (2022). "Study of a General Growth Model". Communications in Nonlinear Science and Numerical Simulation. 107. arXiv: 2402.00882 . doi:10.1016/j.cnsns.2021.106100.
6. Neysens, Patricia; Messens, Winy; Gevers, Dirk; Swings, Jean; De Vuyst, Luc (2003). "Biphasic kinetics of growth and bacteriocin production with Lactobacillus amylovorus DCE 471 occur under stress conditions". Microbiology. 149 (4): 1073–1082. doi: 10.1099/mic.0.25880-0 . PMID   12686649.
7. Chu, Charlene; Han, Christina; Shimizu, Hiromi; Wong, Bonnie (2002). "The Effect of Fructose, Galactose, and Glucose on the Induction of β-Galactosidase in Escherichia coli" (PDF). Journal of Experimental Microbiology and Immunology. 2: 1–5.
8. Tabatabai, M. A.; Eby, W. M.; Singh, K. P.; Bae, S. (2013). "T model of growth and its application in systems of tumor-immunedynamics". Mathematical Biosciences and Engineering. 10 (3): 925–938. doi:10.3934/mbe.2013.10.925. PMC   4476034 . PMID   23906156.
9. Parmoon, Ghasem; Moosavi, Seyed; Poshtdar, Adel; Siadat, Seyed (2020). "Effects of cadmium toxicity on sesame seed germination explained by various nonlinear growth models". Oilseeds & Fats Crops and Lipids. 27 (57): 57. doi: 10.1051/ocl/2020053 .
10. Kronberger, Gabriel; Kammerer, Lukas; Kommenda, Michael (2020). Computer Aided Systems Theory – EUROCAST 2019. Lecture Notes in Computer Science. Vol. 12013. arXiv: 2107.06131 . doi:10.1007/978-3-030-45093-9. ISBN   978-3-030-45092-2. S2CID   215791712.
11. Kamar SH, Msallam BS. Comparative Study between Generalized Maximum Entropy and Bayes Methods to Estimate the Four Parameter Weibull Growth Model. Journal of Probability and Statistics. 2020 Jan 14;2020:1–7.
12. Roehrs T, Bogdan P, Gharaibeh B, et al. (n.d.). "Proliferative heterogeneity in stem cell populations". Live Cell Imaging Laboratory, McGowan Institute for Regenerative Medicine.
13. Eby, Wayne M.; Tabatabai, Mohammad A.; Bursac, Zoran (2010). "Hyperbolastic modeling of tumor growth with a combined treatment of iodoacetate and dimethylsulphoxide". BMC Cancer. 10: 509. doi: 10.1186/1471-2407-10-509 . PMC   2955040 . PMID   20863400.
14. France, James; Kebreab, Ermias, eds. (2008). Mathematical Modelling in Animal Nutrition. Wallingford: CABI. ISBN   9781845933548.
15. Ahmadi, H.; Mottaghitalab, M. (2007). "Hyperbolastic Models as a New Powerful Tool to Describe Broiler Growth Kinetics". Poultry Science. 86 (11): 2461–2465. doi: 10.3382/ps.2007-00086 . PMID   17954598.
16. Tkachuk, S. A.; Pasnichenko, O. S.; Savchok, L. B. (2021). "Approximation of Growth Indicators and Analysis of Individual Growth Curves by Linear Dimensions of Tubular Bones in Chickens of Meat Production Direction During Postnatal Period of Ontogenesis". Ukrainian Journal of Veterinary Sciences. 12 (4). doi: 10.31548/ujvs2021.04.002 . S2CID   245487460.
17. Choi, Taeyoung; Chin, Seongah (2014). "Novel Real-Time Facial Wound Recovery Synthesis Using Subsurface Scattering". The Scientific World Journal. 2014: 1–8. doi: 10.1155/2014/965036 . PMC   4146479 . PMID   25197721.
18. Tabatabai, M.A.; Eby, W.M.; Singh, K.P. (2011). "Hyperbolastic modeling of wound healing". Mathematical and Computer Modelling. 53 (5–6): 755–768. doi: 10.1016/j.mcm.2010.10.013 .
19. Ko, Ung Hyun; Choi, Jongjin; Choung, Jinseung; Moon, Sunghwan; Shin, Jennifer H. (2019). "Physicochemically Tuned Myofibroblasts for Wound Healing Strategy". Scientific Reports. 9 (1): 16070. Bibcode:2019NatSR...916070K. doi:10.1038/s41598-019-52523-9. PMC   6831678 . PMID   31690789.
20. Barrera, Antonio; Román-Román, Patricia; Torres-Ruiz, Francisco (2021). "Hyperbolastic Models from a Stochastic Differential Equation Point of View". Mathematics. 9 (16): 1835. doi: 10.3390/math9161835 .
21. Barrera, Antonio; Román-Román, Patricia; Torres-Ruiz, Francisco (2020). "Diffusion Processes for Weibull-Based Models". Computer Aided Systems Theory – EUROCAST 2019. Lecture Notes in Computer Science. Vol. 12013. pp. 204–210. doi:10.1007/978-3-030-45093-9_25. ISBN   978-3-030-45092-2. S2CID   215792096.
22. Barrera, Antonio; Román-Román, Patricia; Torres-Ruiz, Francisco (2018). "A hyperbolastic type-I diffusion process: Parameter estimation by means of the firefly algorithm". Biosystems. 163: 11–22. arXiv: 2402.03416 . doi:10.1016/j.biosystems.2017.11.001. PMID   29129822.
23. Barrera, Antonio; Román-Roán, Patricia; Torres-Ruiz, Francisco (2020). "Hyperbolastic type-III diffusion process: Obtaining from the generalized Weibull diffusion process". Mathematical Biosciences and Engineering. 17 (1): 814–833. doi: 10.3934/mbe.2020043 . hdl: 10481/58209 . PMID   31731379.
24. Barrera, Antonio; Román-Román, Patricia; Torres-Ruiz, Francisco (2020). "Two Stochastic Differential Equations for Modeling Oscillabolastic-Type Behavior". Mathematics. 8 (2): 155. doi: 10.3390/math8020155 . hdl: 10481/61054 .
25. Stochastic Processes with Applications. 2019. doi: 10.3390/books978-3-03921-729-8 . ISBN   978-3-03921-729-8.
26. Barrera, Antonio; Román-Román, Patricia; Torres-Ruiz, Francisco (2021). "T-Growth Stochastic Model: Simulation and Inference via Metaheuristic Algorithms". Mathematics. 9 (9): 959. doi: 10.3390/math9090959 . hdl: 10481/68288 .
27. Tabatabai, Mohammad A.; Bursac, Zoran; Eby, Wayne M.; Singh, Karan P. (2011). "Mathematical modeling of stem cell proliferation". Medical & Biological Engineering & Computing. 49 (3): 253–262. doi:10.1007/s11517-010-0686-y. PMID   20953843. S2CID   33828764.
28. Eby, Wayne M.; Tabatabai, Mohammad A. (2014). "Methods in Mathematical Modeling for Stem Cells". Stem Cells and Cancer Stem Cells, Volume 12. Vol. 12. pp. 201–217. doi:10.1007/978-94-017-8032-2_18. ISBN   978-94-017-8031-5.
29. Wadkin, L. E.; Orozco-Fuentes, S.; Neganova, I.; Lako, M.; Shukurov, A.; Parker, N. G. (2020). "The recent advances in the mathematical modelling of human pluripotent stem cells". SN Applied Sciences. 2 (2): 276. doi: 10.1007/s42452-020-2070-3 . PMC   7391994 . PMID   32803125.
30. Stem Cells and Cancer Stem Cells, Volume 12. Vol. 12. 2014. doi:10.1007/978-94-017-8032-2. ISBN   978-94-017-8031-5. S2CID   34446642.
31. Tabatabai, Mohammad A.; Kengwoung-Keumo, Jean-Jacques; Eby, Wayne M.; Bae, Sejong; Guemmegne, Juliette T.; Manne, Upender; Fouad, Mona; Partridge, Edward E.; Singh, Karan P. (2014). "Disparities in Cervical Cancer Mortality Rates as Determined by the Longitudinal Hyperbolastic Mixed-Effects Type II Model". PLOS ONE. 9 (9): e107242. Bibcode:2014PLoSO...9j7242T. doi: 10.1371/journal.pone.0107242 . PMC   4167327 . PMID   25226583.
32. Veríssimo, André; Paixão, Laura; Neves, Ana; Vinga, Susana (2013). "BGFit: Management and automated fitting of biological growth curves". BMC Bioinformatics. 14: 283. doi: 10.1186/1471-2105-14-283 . PMC   3848918 . PMID   24067087.
33. Tabatabai, M. A.; Eby, W. M.; Bae, S.; Singh, K. P. (2013). "A flexible multivariable model for Phytoplankton growth". Mathematical Biosciences and Engineering. 10 (3): 913–923. doi: 10.3934/mbe.2013.10.913 . PMID   23906155.
34. Yeasmin, Farhana; Daw, Ranadeep; Chakraborty, Bratati (2021). "A New Growth Rate Measure in Identifying Extended Gompertz Growth Curve and Development of Goodness-of-fit Test". Calcutta Statistical Association Bulletin. 73 (2): 127–145. doi: 10.1177/00080683211037203 .
35. Arif, Samiur (2014). Modeling Stem Cell Population Dynamics (Thesis). Old Dominion University. doi:10.25777/thnx-6q07.
36. Eby, Wayne M.; Oyamakin, Samuel O.; Chukwu, Angela U. (2017). "A new nonlinear model applied to the height-DBH relationship in Gmelina arborea". Forest Ecology and Management. 397: 139–149. doi:10.1016/j.foreco.2017.04.015.
37. Tabatabai, M. A.; Eby, W. M.; Bae, S.; Singh, K. P. (2013). "A flexible multivariable model for Phytoplankton growth". Mathematical Biosciences and Engineering. 10 (3): 913–923. doi: 10.3934/mbe.2013.10.913 . PMID   23906155.
38. Majid, Shahid; Salih, Mohammad; Wasaya, Rozina; Jafri, Wasim (2008). "Predictors of gastrointestinal lesions on endoscopy in iron deficiency anemia without gastrointestinal symptoms". BMC Gastroenterology. 8: 52. doi: 10.1186/1471-230X-8-52 . PMC   2613391 . PMID   18992171.
39. Timmerman, Dirk; Testa, Antonia C.; Bourne, Tom; Ferrazzi, Enrico; Ameye, Lieveke; Konstantinovic, Maja L.; Van Calster, Ben; Collins, William P.; Vergote, Ignace; Van Huffel, Sabine; Valentin, Lil (2005). "Logistic Regression Model to Distinguish Between the Benign and Malignant Adnexal Mass Before Surgery: A Multicenter Study by the International Ovarian Tumor Analysis Group". Journal of Clinical Oncology. 23 (34): 8794–8801. doi: 10.1200/JCO.2005.01.7632 . PMID   16314639.