
In mathematics, Fourier analysis is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer.
In mathematics, the Laplace transform, named after its discoverer Pierre-Simon Laplace, is an integral transform that converts a function of a real variable to a function of a complex variable . The transform has many applications in science and engineering, mostly as a tool for solving linear differential equations. In particular, it transforms ordinary differential equations into algebraic equations and convolution into multiplication. For suitable functions f, the Laplace transform is defined by the integral

In physics, engineering and mathematics, the Fourier transform (FT) is an integral transform that converts a function into a form that describes the frequencies present in the original function. The output of the transform is a complex-valued function of frequency. The term Fourier transform refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made the Fourier transform is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches.
In mathematics, the convolution theorem states that under suitable conditions the Fourier transform of a convolution of two functions is the pointwise product of their Fourier transforms. More generally, convolution in one domain equals point-wise multiplication in the other domain. Other versions of the convolution theorem are applicable to various Fourier-related transforms.
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of definition of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where the infinite series representation which initially defined the function becomes divergent.
In fractional calculus, an area of mathematical analysis, the differintegral is a combined differentiation/integration operator. Applied to a function ƒ, the q-differintegral of f, here denoted by
The Laplace–Stieltjes transform, named for Pierre-Simon Laplace and Thomas Joannes Stieltjes, is an integral transform similar to the Laplace transform. For real-valued functions, it is the Laplace transform of a Stieltjes measure, however it is often defined for functions with values in a Banach space. It is useful in a number of areas of mathematics, including functional analysis, and certain areas of theoretical and applied probability.
In mathematics, the Fourier inversion theorem says that for many types of functions it is possible to recover a function from its Fourier transform. Intuitively it may be viewed as the statement that if we know all frequency and phase information about a wave then we may reconstruct the original wave precisely.
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform. This integral transform is closely connected to the theory of Dirichlet series, and is often used in number theory, mathematical statistics, and the theory of asymptotic expansions; it is closely related to the Laplace transform and the Fourier transform, and the theory of the gamma function and allied special functions.
In mathematics, the Poisson summation formula is an equation that relates the Fourier series coefficients of the periodic summation of a function to values of the function's continuous Fourier transform. Consequently, the periodic summation of a function is completely defined by discrete samples of the original function's Fourier transform. And conversely, the periodic summation of a function's Fourier transform is completely defined by discrete samples of the original function. The Poisson summation formula was discovered by Siméon Denis Poisson and is sometimes called Poisson resummation.

In mathematics, the Radon transform is the integral transform which takes a function f defined on the plane to a function Rf defined on the (two-dimensional) space of lines in the plane, whose value at a particular line is equal to the line integral of the function over that line. The transform was introduced in 1917 by Johann Radon, who also provided a formula for the inverse transform. Radon further included formulas for the transform in three dimensions, in which the integral is taken over planes. It was later generalized to higher-dimensional Euclidean spaces and more broadly in the context of integral geometry. The complex analogue of the Radon transform is known as the Penrose transform. The Radon transform is widely applicable to tomography, the creation of an image from the projection data associated with cross-sectional scans of an object.
In mathematics, the Riemann–Liouville integral associates with a real function another function Iαf of the same kind for each value of the parameter α > 0. The integral is a manner of generalization of the repeated antiderivative of f in the sense that for positive integer values of α, Iαf is an iterated antiderivative of f of order α. The Riemann–Liouville integral is named for Bernhard Riemann and Joseph Liouville, the latter of whom was the first to consider the possibility of fractional calculus in 1832. The operator agrees with the Euler transform, after Leonhard Euler, when applied to analytic functions. It was generalized to arbitrary dimensions by Marcel Riesz, who introduced the Riesz potential.

In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet, one of which is the improper integral of the sinc function over the positive real line:
In mathematics, the Mellin inversion formula tells us conditions under which the inverse Mellin transform, or equivalently the inverse two-sided Laplace transform, are defined and recover the transformed function.
In mathematics, the two-sided Laplace transform or bilateral Laplace transform is an integral transform equivalent to probability's moment-generating function. Two-sided Laplace transforms are closely related to the Fourier transform, the Mellin transform, the Z-transform and the ordinary or one-sided Laplace transform. If f(t) is a real- or complex-valued function of the real variable t defined for all real numbers, then the two-sided Laplace transform is defined by the integral
In mathematics, the explicit formulae for L-functions are relations between sums over the complex number zeroes of an L-function and sums over prime powers, introduced by Riemann (1859) for the Riemann zeta function. Such explicit formulae have been applied also to questions on bounding the discriminant of an algebraic number field, and the conductor of a number field.
In mathematics, the Fourier sine and cosine transforms are forms of the Fourier transform that do not use complex numbers or require negative frequency. They are the forms originally used by Joseph Fourier and are still preferred in some applications, such as signal processing or statistics.
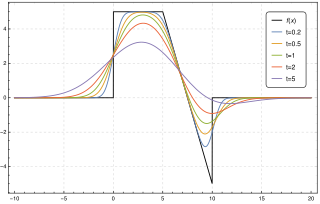
In mathematics, the Weierstrass transform of a function f : R → R, named after Karl Weierstrass, is a "smoothed" version of f(x) obtained by averaging the values of f, weighted with a Gaussian centered at x.
In mathematical analysis, the final value theorem (FVT) is one of several similar theorems used to relate frequency domain expressions to the time domain behavior as time approaches infinity. Mathematically, if in continuous time has (unilateral) Laplace transform , then a final value theorem establishes conditions under which
In analytic number theory, a Dirichlet series, or Dirichlet generating function (DGF), of a sequence is a common way of understanding and summing arithmetic functions in a meaningful way. A little known, or at least often forgotten about, way of expressing formulas for arithmetic functions and their summatory functions is to perform an integral transform that inverts the operation of forming the DGF of a sequence. This inversion is analogous to performing an inverse Z-transform to the generating function of a sequence to express formulas for the series coefficients of a given ordinary generating function.









