In statistics and statistical physics, the Metropolis–Hastings algorithm is a Markov chain Monte Carlo (MCMC) method for obtaining a sequence of random samples from a probability distribution from which direct sampling is difficult. This sequence can be used to approximate the distribution or to compute an integral. Metropolis–Hastings and other MCMC algorithms are generally used for sampling from multi-dimensional distributions, especially when the number of dimensions is high. For single-dimensional distributions, there are usually other methods that can directly return independent samples from the distribution, and these are free from the problem of autocorrelated samples that is inherent in MCMC methods.
In finance, the binomial options pricing model (BOPM) provides a generalizable numerical method for the valuation of options. Essentially, the model uses a "discrete-time" model of the varying price over time of the underlying financial instrument, addressing cases where the closed-form Black–Scholes formula is wanting.
In plasma physics, the particle-in-cell (PIC) method refers to a technique used to solve a certain class of partial differential equations. In this method, individual particles in a Lagrangian frame are tracked in continuous phase space, whereas moments of the distribution such as densities and currents are computed simultaneously on Eulerian (stationary) mesh points.
The classical XY model is a lattice model of statistical mechanics. In general, the XY model can be seen as a specialization of Stanley's n-vector model for n = 2.
The Eyring equation is an equation used in chemical kinetics to describe changes in the rate of a chemical reaction against temperature. It was developed almost simultaneously in 1935 by Henry Eyring, Meredith Gwynne Evans and Michael Polanyi. The equation follows from the transition state theory, also known as activated-complex theory. If one assumes a constant enthalpy of activation and constant entropy of activation, the Eyring equation is similar to the empirical Arrhenius equation, despite the Arrhenius equation being empirical and the Eyring equation based on statistical mechanical justification.
In probability theory, the Gillespie algorithm generates a statistically correct trajectory of a stochastic equation system for which the reaction rates are known. It was created by Joseph L. Doob and others, presented by Dan Gillespie in 1976, and popularized in 1977 in a paper where he uses it to simulate chemical or biochemical systems of reactions efficiently and accurately using limited computational power. As computers have become faster, the algorithm has been used to simulate increasingly complex systems. The algorithm is particularly useful for simulating reactions within cells, where the number of reagents is low and keeping track of every single reaction is computationally feasible. Mathematically, it is a variant of a dynamic Monte Carlo method and similar to the kinetic Monte Carlo methods. It is used heavily in computational systems biology.
A stochastic simulation is a simulation of a system that has variables that can change stochastically (randomly) with individual probabilities.

Umbrella sampling is a technique in computational physics and chemistry, used to improve sampling of a system where ergodicity is hindered by the form of the system's energy landscape. It was first suggested by Torrie and Valleau in 1977. It is a particular physical application of the more general importance sampling in statistics.
In thermodynamics, the excess chemical potential is defined as the difference between the chemical potential of a given species and that of an ideal gas under the same conditions . The chemical potential of a particle species is therefore given by an ideal part and an excess part.
The Wang and Landau algorithm, proposed by Fugao Wang and David P. Landau, is a Monte Carlo method designed to estimate the density of states of a system. The method performs a non-Markovian random walk to build the density of states by quickly visiting all the available energy spectrum. The Wang and Landau algorithm is an important method to obtain the density of states required to perform a multicanonical simulation.
The BFM is a lattice model for simulating the conformation and dynamics of polymer systems. There are two versions of the BFM used: The earlier version was first introduced by I. Carmesin and Kurt Kremer in 1988, and the later version by J. Scott Shaffer in 1994. Conversion between models is possible.
The Swendsen–Wang algorithm is the first non-local or cluster algorithm for Monte Carlo simulation for large systems near criticality. It has been introduced by Robert Swendsen and Jian-Sheng Wang in 1987 at Carnegie Mellon.
The Nosé–Hoover thermostat is a deterministic algorithm for constant-temperature molecular dynamics simulations. It was originally developed by Nosé and was improved further by Hoover. Although the heat bath of Nosé–Hoover thermostat consists of only one imaginary particle, simulation systems achieve realistic constant-temperature condition. Therefore, the Nosé–Hoover thermostat has been commonly used as one of the most accurate and efficient methods for constant-temperature molecular dynamics simulations.
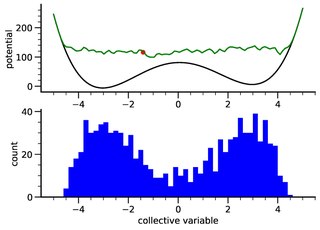
Metadynamics is a computer simulation method in computational physics, chemistry and biology. It is used to estimate the free energy and other state functions of a system, where ergodicity is hindered by the form of the system's energy landscape. It was first suggested by Alessandro Laio and Michele Parrinello in 2002 and is usually applied within molecular dynamics simulations. MTD closely resembles a number of newer methods such as adaptively biased molecular dynamics, adaptive reaction coordinate forces and local elevation umbrella sampling. More recently, both the original and well-tempered metadynamics were derived in the context of importance sampling and shown to be a special case of the adaptive biasing potential setting. MTD is related to the Wang–Landau sampling.
The Monte Carlo method for electron transport is a semiclassical Monte Carlo (MC) approach of modeling semiconductor transport. Assuming the carrier motion consists of free flights interrupted by scattering mechanisms, a computer is utilized to simulate the trajectories of particles as they move across the device under the influence of an electric field using classical mechanics. The scattering events and the duration of particle flight is determined through the use of random numbers.
Local elevation is a technique used in computational chemistry or physics, mainly in the field of molecular simulation. It was developed in 1994 by Huber, Torda and van Gunsteren to enhance the searching of conformational space in molecular dynamics simulations and is available in the GROMOS software for molecular dynamics simulation. The method was, together with the conformational flooding method, the first to introduce memory dependence into molecular simulations. Many recent methods build on the principles of the local elevation technique, including the Engkvist-Karlström, adaptive biasing force, Wang–Landau, metadynamics, adaptively biased molecular dynamics, adaptive reaction coordinate forces, and local elevation umbrella sampling methods. The basic principle of the method is to add a memory-dependent potential energy term in the simulation so as to prevent the simulation to revisit already sampled configurations, which leads to the increased probability of discovering new configurations. The method can be seen as a continuous variant of the Tabu search method.
The Hamiltonian Monte Carlo algorithm is a Markov chain Monte Carlo method for obtaining a sequence of random samples which converge to being distributed according to a target probability distribution for which direct sampling is difficult. This sequence can be used to estimate integrals with respect to the target distribution.
In statistics and physics, multicanonical ensemble is a Markov chain Monte Carlo sampling technique that uses the Metropolis–Hastings algorithm to compute integrals where the integrand has a rough landscape with multiple local minima. It samples states according to the inverse of the density of states, which has to be known a priori or be computed using other techniques like the Wang and Landau algorithm. Multicanonical sampling is an important technique for spin systems like the Ising model or spin glasses.
In mathematics, the walk-on-spheres method (WoS) is a numerical probabilistic algorithm, or Monte-Carlo method, used mainly in order to approximate the solutions of some specific boundary value problem for partial differential equations (PDEs). The WoS method was first introduced by Mervin E. Muller in 1956 to solve Laplace's equation, and was since then generalized to other problems.
In mathematics and physics, surface growth refers to models used in the dynamical study of the growth of a surface, usually by means of a stochastic differential equation of a field.