The Beer-Lambert law is commonly applied to chemical analysis measurements to determine the concentration of chemical species that absorb light. It is often referred to as Beer's law. In physics, the Bouguer–Lambert law is an empirical law which relates the extinction or attenuation of light to the properties of the material through which the light is travelling. It had its first use in astronomical extinction. The fundamental law of extinction is sometimes called the Beer-Bouguer-Lambert law or the Bouguer-Beer-Lambert law or merely the extinction law. The extinction law is also used in understanding attenuation in physical optics, for photons, neutrons, or rarefied gases. In mathematical physics, this law arises as a solution of the BGK equation.
Circular dichroism (CD) is dichroism involving circularly polarized light, i.e., the differential absorption of left- and right-handed light. Left-hand circular (LHC) and right-hand circular (RHC) polarized light represent two possible spin angular momentum states for a photon, and so circular dichroism is also referred to as dichroism for spin angular momentum. This phenomenon was discovered by Jean-Baptiste Biot, Augustin Fresnel, and Aimé Cotton in the first half of the 19th century. Circular dichroism and circular birefringence are manifestations of optical activity. It is exhibited in the absorption bands of optically active chiral molecules. CD spectroscopy has a wide range of applications in many different fields. Most notably, UV CD is used to investigate the secondary structure of proteins. UV/Vis CD is used to investigate charge-transfer transitions. Near-infrared CD is used to investigate geometric and electronic structure by probing metal d→d transitions. Vibrational circular dichroism, which uses light from the infrared energy region, is used for structural studies of small organic molecules, and most recently proteins and DNA.
In mathematical optimization, the method of Lagrange multipliers is a strategy for finding the local maxima and minima of a function subject to equation constraints. It is named after the mathematician Joseph-Louis Lagrange.
In engineering, deformation refers to the change in size or shape of an object. Displacements are the absolute change in position of a point on the object. Deflection is the relative change in external displacements on an object. Strain is the relative internal change in shape of an infinitesimal cube of material and can be expressed as a non-dimensional change in length or angle of distortion of the cube. Strains are related to the forces acting on the cube, which are known as stress, by a stress-strain curve. The relationship between stress and strain is generally linear and reversible up until the yield point and the deformation is elastic. The linear relationship for a material is known as Young's modulus. Above the yield point, some degree of permanent distortion remains after unloading and is termed plastic deformation. The determination of the stress and strain throughout a solid object is given by the field of strength of materials and for a structure by structural analysis.
In mathematics, a fractal dimension is a term invoked in the science of geometry to provide a rational statistical index of complexity detail in a pattern. A fractal pattern changes with the scale at which it is measured. It is also a measure of the space-filling capacity of a pattern, and it tells how a fractal scales differently, in a fractal (non-integer) dimension.
The Ising model, named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that represent magnetic dipole moments of atomic "spins" that can be in one of two states. The spins are arranged in a graph, usually a lattice, allowing each spin to interact with its neighbors. Neighboring spins that agree have a lower energy than those that disagree; the system tends to the lowest energy but heat disturbs this tendency, thus creating the possibility of different structural phases. The model allows the identification of phase transitions as a simplified model of reality. The two-dimensional square-lattice Ising model is one of the simplest statistical models to show a phase transition.

An eigenface is the name given to a set of eigenvectors when used in the computer vision problem of human face recognition. The approach of using eigenfaces for recognition was developed by Sirovich and Kirby and used by Matthew Turk and Alex Pentland in face classification. The eigenvectors are derived from the covariance matrix of the probability distribution over the high-dimensional vector space of face images. The eigenfaces themselves form a basis set of all images used to construct the covariance matrix. This produces dimension reduction by allowing the smaller set of basis images to represent the original training images. Classification can be achieved by comparing how faces are represented by the basis set.

In fractal geometry, the Minkowski–Bouligand dimension, also known as Minkowski dimension or box-counting dimension, is a way of determining the fractal dimension of a set in a Euclidean space , or more generally in a metric space . It is named after the Polish mathematician Hermann Minkowski and the French mathematician Georges Bouligand.
In physics, mathematics and statistics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor, and thus represent a universality.

A granular material is a conglomeration of discrete solid, macroscopic particles characterized by a loss of energy whenever the particles interact. The constituents that compose granular material are large enough such that they are not subject to thermal motion fluctuations. Thus, the lower size limit for grains in granular material is about 1 μm. On the upper size limit, the physics of granular materials may be applied to ice floes where the individual grains are icebergs and to asteroid belts of the Solar System with individual grains being asteroids.
In graph theory, a graph is said to be a pseudorandom graph if it obeys certain properties that random graphs obey with high probability. There is no concrete definition of graph pseudorandomness, but there are many reasonable characterizations of pseudorandomness one can consider.
The Poisson–Boltzmann equation describes the distribution of the electric potential in solution in the direction normal to a charged surface. This distribution is important to determine how the electrostatic interactions will affect the molecules in solution. The Poisson–Boltzmann equation is derived via mean-field assumptions. From the Poisson–Boltzmann equation many other equations have been derived with a number of different assumptions.

A multifractal system is a generalization of a fractal system in which a single exponent is not enough to describe its dynamics; instead, a continuous spectrum of exponents is needed.
In the fields of computer vision and image analysis, the Harris affine region detector belongs to the category of feature detection. Feature detection is a preprocessing step of several algorithms that rely on identifying characteristic points or interest points so to make correspondences between images, recognize textures, categorize objects or build panoramas.
In probability and statistics, the Tweedie distributions are a family of probability distributions which include the purely continuous normal, gamma and inverse Gaussian distributions, the purely discrete scaled Poisson distribution, and the class of compound Poisson–gamma distributions which have positive mass at zero, but are otherwise continuous. Tweedie distributions are a special case of exponential dispersion models and are often used as distributions for generalized linear models.

Viscoplasticity is a theory in continuum mechanics that describes the rate-dependent inelastic behavior of solids. Rate-dependence in this context means that the deformation of the material depends on the rate at which loads are applied. The inelastic behavior that is the subject of viscoplasticity is plastic deformation which means that the material undergoes unrecoverable deformations when a load level is reached. Rate-dependent plasticity is important for transient plasticity calculations. The main difference between rate-independent plastic and viscoplastic material models is that the latter exhibit not only permanent deformations after the application of loads but continue to undergo a creep flow as a function of time under the influence of the applied load.
Fractal analysis is assessing fractal characteristics of data. It consists of several methods to assign a fractal dimension and other fractal characteristics to a dataset which may be a theoretical dataset, or a pattern or signal extracted from phenomena including topography, natural geometric objects, ecology and aquatic sciences, sound, market fluctuations, heart rates, frequency domain in electroencephalography signals, digital images, molecular motion, and data science. Fractal analysis is now widely used in all areas of science. An important limitation of fractal analysis is that arriving at an empirically determined fractal dimension does not necessarily prove that a pattern is fractal; rather, other essential characteristics have to be considered. Fractal analysis is valuable in expanding our knowledge of the structure and function of various systems, and as a potential tool to mathematically assess novel areas of study. Fractal calculus was formulated which is a generalization of ordinary calculus.
The near-infrared (NIR) window defines the range of wavelengths from 650 to 1350 nanometre (nm) where light has its maximum depth of penetration in tissue. Within the NIR window, scattering is the most dominant light-tissue interaction, and therefore the propagating light becomes diffused rapidly. Since scattering increases the distance travelled by photons within tissue, the probability of photon absorption also increases. Because scattering has weak dependence on wavelength, the NIR window is primarily limited by the light absorption of blood at short wavelengths and water at long wavelengths. The technique using this window is called NIRS. Medical imaging techniques such as fluorescence image-guided surgery often make use of the NIR window to detect deep structures.
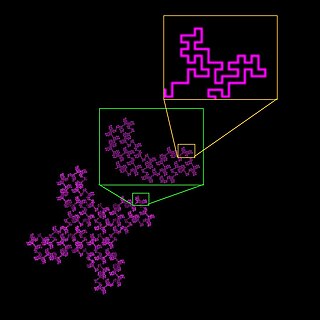
Box counting is a method of gathering data for analyzing complex patterns by breaking a dataset, object, image, etc. into smaller and smaller pieces, typically "box"-shaped, and analyzing the pieces at each smaller scale. The essence of the process has been compared to zooming in or out using optical or computer based methods to examine how observations of detail change with scale. In box counting, however, rather than changing the magnification or resolution of a lens, the investigator changes the size of the element used to inspect the object or pattern. Computer based box counting algorithms have been applied to patterns in 1-, 2-, and 3-dimensional spaces. The technique is usually implemented in software for use on patterns extracted from digital media, although the fundamental method can be used to investigate some patterns physically. The technique arose out of and is used in fractal analysis. It also has application in related fields such as lacunarity and multifractal analysis.

In semiconductor electrochemistry, a Mott–Schottky plot describes the reciprocal of the square of capacitance versus the potential difference between bulk semiconductor and bulk electrolyte. In many theories, and in many experimental measurements, the plot is linear. The use of Mott–Schottky plots to determine system properties is termed Mott–Schottky analysis.














































