Control theory is a field of control engineering and applied mathematics that deals with the control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any delay, overshoot, or steady-state error and ensuring a level of control stability; often with the aim to achieve a degree of optimality.
The logistic map is a polynomial mapping of degree 2, often referred to as an archetypal example of how complex, chaotic behaviour can arise from very simple nonlinear dynamical equations. The map, initially utilized by Edward Lorenz in the 1960s to showcase irregular solutions, was popularized in a 1976 paper by the biologist Robert May, in part as a discrete-time demographic model analogous to the logistic equation written down by Pierre François Verhulst. Mathematically, the logistic map is written
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists since most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems.

In mathematics, the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories. Quantitatively, two trajectories in phase space with initial separation vector diverge at a rate given by

In the mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain close even if slightly disturbed.
Various types of stability may be discussed for the solutions of differential equations or difference equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Aleksandr Lyapunov. In simple terms, if the solutions that start out near an equilibrium point stay near forever, then is Lyapunov stable. More strongly, if is Lyapunov stable and all solutions that start out near converge to , then is said to be asymptotically stable. The notion of exponential stability guarantees a minimal rate of decay, i.e., an estimate of how quickly the solutions converge. The idea of Lyapunov stability can be extended to infinite-dimensional manifolds, where it is known as structural stability, which concerns the behavior of different but "nearby" solutions to differential equations. Input-to-state stability (ISS) applies Lyapunov notions to systems with inputs.
A stochastic differential equation (SDE) is a differential equation in which one or more of the terms is a stochastic process, resulting in a solution which is also a stochastic process. SDEs have many applications throughout pure mathematics and are used to model various behaviours of stochastic models such as stock prices, random growth models or physical systems that are subjected to thermal fluctuations.

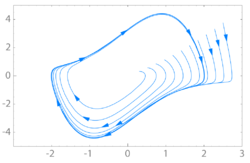
In the study of dynamical systems, the van der Pol oscillator is a non-conservative, oscillating system with non-linear damping. It evolves in time according to the second-order differential equation

Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations occur in both continuous systems and discrete systems.
In mathematics, delay differential equations (DDEs) are a type of differential equation in which the derivative of the unknown function at a certain time is given in terms of the values of the function at previous times. DDEs are also called time-delay systems, systems with aftereffect or dead-time, hereditary systems, equations with deviating argument, or differential-difference equations. They belong to the class of systems with the functional state, i.e. partial differential equations (PDEs) which are infinite dimensional, as opposed to ordinary differential equations (ODEs) having a finite dimensional state vector. Four points may give a possible explanation of the popularity of DDEs:
- Aftereffect is an applied problem: it is well known that, together with the increasing expectations of dynamic performances, engineers need their models to behave more like the real process. Many processes include aftereffect phenomena in their inner dynamics. In addition, actuators, sensors, and communication networks that are now involved in feedback control loops introduce such delays. Finally, besides actual delays, time lags are frequently used to simplify very high order models. Then, the interest for DDEs keeps on growing in all scientific areas and, especially, in control engineering.
- Delay systems are still resistant to many classical controllers: one could think that the simplest approach would consist in replacing them by some finite-dimensional approximations. Unfortunately, ignoring effects which are adequately represented by DDEs is not a general alternative: in the best situation, it leads to the same degree of complexity in the control design. In worst cases, it is potentially disastrous in terms of stability and oscillations.
- Voluntary introduction of delays can benefit the control system.
- In spite of their complexity, DDEs often appear as simple infinite-dimensional models in the very complex area of partial differential equations (PDEs).
In mathematics, more specifically in the study of dynamical systems and differential equations, a Liénard equation is a type of second-order ordinary differential equation named after the French physicist Alfred-Marie Liénard.

In mathematics and physics, the Kadomtsev–Petviashvili equation is a partial differential equation to describe nonlinear wave motion. Named after Boris Borisovich Kadomtsev and Vladimir Iosifovich Petviashvili, the KP equation is usually written as
In mathematics, especially in the study of dynamical systems, a limit set is the state a dynamical system reaches after an infinite amount of time has passed, by either going forward or backwards in time. Limit sets are important because they can be used to understand the long term behavior of a dynamical system. A system that has reached its limiting set is said to be at equilibrium.
An -superprocess, , within mathematics probability theory is a stochastic process on that is usually constructed as a special limit of near-critical branching diffusions.
The Lyapunov–Malkin theorem is a mathematical theorem detailing stability of nonlinear systems.

The theta model, or Ermentrout–Kopell canonical model, is a biological neuron model originally developed to mathematically describe neurons in the animal Aplysia. The model is particularly well-suited to describe neural bursting, which is characterized by periodic transitions between rapid oscillations in the membrane potential followed by quiescence. This bursting behavior is often found in neurons responsible for controlling and maintaining steady rhythms such as breathing, swimming, and digesting. Of the three main classes of bursting neurons, the theta model describes parabolic bursting, which is characterized by a parabolic frequency curve during each burst.
In probability theory, a McKean–Vlasov process is a stochastic process described by a stochastic differential equation where the coefficients of the diffusion depend on the distribution of the solution itself. The equations are a model for Vlasov equation and were first studied by Henry McKean in 1966. It is an example of propagation of chaos, in that it can be obtained as a limit of a mean-field system of interacting particles: as the number of particles tends to infinity, the interactions between any single particle and the rest of the pool will only depend on the particle itself.
Input-to-state stability (ISS) is a stability notion widely used to study stability of nonlinear control systems with external inputs. Roughly speaking, a control system is ISS if it is globally asymptotically stable in the absence of external inputs and if its trajectories are bounded by a function of the size of the input for all sufficiently large times. The importance of ISS is due to the fact that the concept has bridged the gap between input–output and state-space methods, widely used within the control systems community.
Phase reduction is a method used to reduce a multi-dimensional dynamical equation describing a nonlinear limit cycle oscillator into a one-dimensional phase equation. Many phenomena in our world such as chemical reactions, electric circuits, mechanical vibrations, cardiac cells, and spiking neurons are examples of rhythmic phenomena, and can be considered as nonlinear limit cycle oscillators.
In mathematics and mathematical biology, the Mackey–Glass equations, named after Michael Mackey and Leon Glass, refer to a family of delay differential equations whose behaviour manages to mimic both healthy and pathological behaviour in certain biological contexts, controlled by the equation's parameters. Originally, they were used to model the variation in the relative quantity of mature cells in the blood. The equations are defined as: