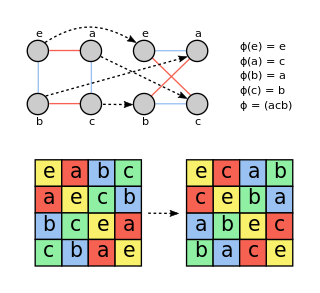
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism group. It is, loosely speaking, the symmetry group of the object.

In mathematics, a field is a set on which addition, subtraction, multiplication, and division are defined and behave as the corresponding operations on rational and real numbers. A field is thus a fundamental algebraic structure which is widely used in algebra, number theory, and many other areas of mathematics.
In mathematics, in the area of abstract algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension. The study of field extensions and their relationship to the polynomials that give rise to them via Galois groups is called Galois theory, so named in honor of Évariste Galois who first discovered them.

In abstract algebra, group theory studies the algebraic structures known as groups. The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces, can all be seen as groups endowed with additional operations and axioms. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic groups and Lie groups are two branches of group theory that have experienced advances and have become subject areas in their own right.

In abstract algebra, a cyclic group or monogenous group is a group, denoted Cn, that is generated by a single element. That is, it is a set of invertible elements with a single associative binary operation, and it contains an element g such that every other element of the group may be obtained by repeatedly applying the group operation to g or its inverse. Each element can be written as an integer power of g in multiplicative notation, or as an integer multiple of g in additive notation. This element g is called a generator of the group.

In mathematics, Galois theory, originally introduced by Évariste Galois, provides a connection between field theory and group theory. This connection, the fundamental theorem of Galois theory, allows reducing certain problems in field theory to group theory, which makes them simpler and easier to understand.
In mathematics, class field theory (CFT) is the fundamental branch of algebraic number theory whose goal is to describe all the abelian Galois extensions of local and global fields using objects associated to the ground field.
In mathematics, a Galois extension is an algebraic field extension E/F that is normal and separable; or equivalently, E/F is algebraic, and the field fixed by the automorphism group Aut(E/F) is precisely the base field F. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.
In mathematics, a Galois module is a G-module, with G being the Galois group of some extension of fields. The term Galois representation is frequently used when the G-module is a vector space over a field or a free module over a ring in representation theory, but can also be used as a synonym for G-module. The study of Galois modules for extensions of local or global fields and their group cohomology is an important tool in number theory.
In mathematics, a duality translates concepts, theorems or mathematical structures into other concepts, theorems or structures in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. Such involutions sometimes have fixed points, so that the dual of A is A itself. For example, Desargues' theorem is self-dual in this sense under the standard duality in projective geometry.
In mathematics, differential Galois theory studies the Galois groups of differential equations.
In mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups. A Galois group G associated to a field extension L/K acts in a natural way on some abelian groups, for example those constructed directly from L, but also through other Galois representations that may be derived by more abstract means. Galois cohomology accounts for the way in which taking Galois-invariant elements fails to be an exact functor.
In mathematics, a dessin d'enfant is a type of graph embedding used to study Riemann surfaces and to provide combinatorial invariants for the action of the absolute Galois group of the rational numbers. The name of these embeddings is French for a "child's drawing"; its plural is either dessins d'enfant, "child's drawings", or dessins d'enfants, "children's drawings".

Øystein Ore was a Norwegian mathematician known for his work in ring theory, Galois connections, graph theory, and the history of mathematics.
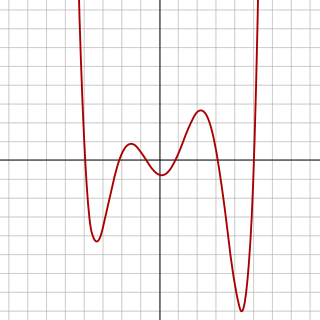
In algebra, a sexticpolynomial is a polynomial of degree six. A sextic equation is a polynomial equation of degree six—that is, an equation whose left hand side is a sextic polynomial and whose right hand side is zero. More precisely, it has the form:

Algebraic combinatorics is an area of mathematics that employs methods of abstract algebra, notably group theory and representation theory, in various combinatorial contexts and, conversely, applies combinatorial techniques to problems in algebra.
There are many terms in mathematics that begin with cyclic:
In mathematics, especially (higher) category theory, higher-dimensional algebra is the study of categorified structures. It has applications in nonabelian algebraic topology, and generalizes abstract algebra.
Mathematics is a broad subject that is commonly divided in many areas that may be defined by their objects of study, by the used methods, or by both. For example, analytic number theory is a subarea of number theory devoted to the use of methods of analysis for the study of natural numbers.
Yasutaka Ihara is a Japanese mathematician and professor emeritus at the Research Institute for Mathematical Sciences. His work in number theory includes Ihara's lemma and the Ihara zeta function.