
In mathematics, the gamma function is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer n,

In complex analysis, the residue theorem, sometimes called Cauchy's residue theorem, is a powerful tool to evaluate line integrals of analytic functions over closed curves; it can often be used to compute real integrals and infinite series as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula. The residue theorem should not be confused with special cases of the generalized Stokes' theorem; however, the latter can be used as an ingredient of its proof.

In mathematics, Stirling's approximation is an asymptotic approximation for factorials. It is a good approximation, leading to accurate results even for small values of . It is named after James Stirling, though a related but less precise result was first stated by Abraham de Moivre.
Integration is the basic operation in integral calculus. While differentiation has straightforward rules by which the derivative of a complicated function can be found by differentiating its simpler component functions, integration does not, so tables of known integrals are often useful. This page lists some of the most common antiderivatives.

In mathematics, trigonometric integrals are a family of nonelementary integrals involving trigonometric functions.

In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number x. It is denoted by π(x) (unrelated to the number π).

In the physical sciences, the Airy function (or Airy function of the first kind) Ai(x) is a special function named after the British astronomer George Biddell Airy (1801–1892). The function Ai(x) and the related function Bi(x), are linearly independent solutions to the differential equation

In mathematics, the digamma function is defined as the logarithmic derivative of the gamma function:

In mathematics, the upper and lower incomplete gamma functions are types of special functions which arise as solutions to various mathematical problems such as certain integrals.

In mathematics, the polylogarithm (also known as Jonquière's function, for Alfred Jonquière) is a special function Lis(z) of order s and argument z. Only for special values of s does the polylogarithm reduce to an elementary function such as the natural logarithm or a rational function. In quantum statistics, the polylogarithm function appears as the closed form of integrals of the Fermi–Dirac distribution and the Bose–Einstein distribution, and is also known as the Fermi–Dirac integral or the Bose–Einstein integral. In quantum electrodynamics, polylogarithms of positive integer order arise in the calculation of processes represented by higher-order Feynman diagrams.
In mathematical analysis, asymptotic analysis, also known as asymptotics, is a method of describing limiting behavior.
In mathematics, an asymptotic expansion, asymptotic series or Poincaré expansion is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular, often infinite, point. Investigations by Dingle (1973) revealed that the divergent part of an asymptotic expansion is latently meaningful, i.e. contains information about the exact value of the expanded function.

In mathematics, the exponential integral Ei is a special function on the complex plane.

In mathematics, the Barnes G-functionG(z) is a function that is an extension of superfactorials to the complex numbers. It is related to the gamma function, the K-function and the Glaisher–Kinkelin constant, and was named after mathematician Ernest William Barnes. It can be written in terms of the double gamma function.
In mathematics, the explicit formulae for L-functions are relations between sums over the complex number zeroes of an L-function and sums over prime powers, introduced by Riemann (1859) for the Riemann zeta function. Such explicit formulae have been applied also to questions on bounding the discriminant of an algebraic number field, and the conductor of a number field.
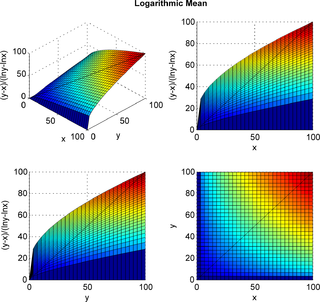
In mathematics, the logarithmic mean is a function of two non-negative numbers which is equal to their difference divided by the logarithm of their quotient. This calculation is applicable in engineering problems involving heat and mass transfer.
Gregory coefficientsGn, also known as reciprocal logarithmic numbers, Bernoulli numbers of the second kind, or Cauchy numbers of the first kind, are the rational numbers that occur in the Maclaurin series expansion of the reciprocal logarithm





































