
In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.
In mathematics, a symmetric matrix with real entries is positive-definite if the real number is positive for every nonzero real column vector where is the transpose of . More generally, a Hermitian matrix is positive-definite if the real number is positive for every nonzero complex column vector where denotes the conjugate transpose of
Kinematics is a subfield of physics, developed in classical mechanics, that describes the motion of points, bodies (objects), and systems of bodies without considering the forces that cause them to move. Kinematics, as a field of study, is often referred to as the "geometry of motion" and is occasionally seen as a branch of mathematics. A kinematics problem begins by describing the geometry of the system and declaring the initial conditions of any known values of position, velocity and/or acceleration of points within the system. Then, using arguments from geometry, the position, velocity and acceleration of any unknown parts of the system can be determined. The study of how forces act on bodies falls within kinetics, not kinematics. For further details, see analytical dynamics.

In mathematics, particularly in linear algebra, matrix multiplication is a binary operation that produces a matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The resulting matrix, known as the matrix product, has the number of rows of the first and the number of columns of the second matrix. The product of matrices A and B is denoted as AB.

The moment of inertia, otherwise known as the mass moment of inertia, angular mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is a quantity that determines the torque needed for a desired angular acceleration about a rotational axis, akin to how mass determines the force needed for a desired acceleration. It depends on the body's mass distribution and the axis chosen, with larger moments requiring more torque to change the body's rate of rotation.
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition.
In the mathematical field of differential geometry, a metric tensor allows defining distances and angles near each point of a surface, in the same way as inner product allows defining distances and angles in Euclidean spaces. More precisely, a metric tensor at a point of a manifold is a bilinear form defined on the tangent space at this point.
In linear algebra, the adjugate or classical adjoint of a square matrix is the transpose of its cofactor matrix. It is also occasionally known as adjunct matrix, though this nomenclature appears to have decreased in usage. The adjugate has sometimes been called the "adjoint", but today the "adjoint" of a matrix normally refers to its corresponding adjoint operator, which is its conjugate transpose.
In linear algebra, a QR decomposition, also known as a QR factorization or QU factorization, is a decomposition of a matrix A into a product A = QR of an orthogonal matrix Q and an upper triangular matrix R. QR decomposition is often used to solve the linear least squares problem and is the basis for a particular eigenvalue algorithm, the QR algorithm.
In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of the algebra produces the Hodge dual of the element. This map was introduced by W. V. D. Hodge.
In numerical analysis, one of the most important problems is designing efficient and stable algorithms for finding the eigenvalues of a matrix. These eigenvalue algorithms may also find eigenvectors.
In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation in Euclidean space. For example, using the convention below, the matrix

In geometry, Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two rotations is also a rotation. Therefore the set of rotations has a group structure, known as a rotation group.
In linear algebra, the generalized singular value decomposition (GSVD) is the name of two different techniques based on the singular value decomposition (SVD). The two versions differ because one version decomposes two matrices and the other version uses a set of constraints imposed on the left and right singular vectors of a single-matrix SVD.
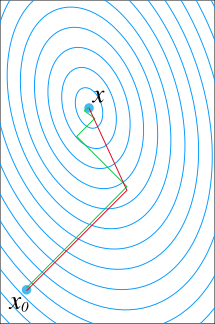
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-definite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving partial differential equations or optimization problems.

In numerical analysis, the Crank–Nicolson method is a finite difference method used for numerically solving the heat equation and similar partial differential equations. It is a second-order method in time. It is implicit in time, can be written as an implicit Runge–Kutta method, and it is numerically stable. The method was developed by John Crank and Phyllis Nicolson in the mid 20th century.

In electromagnetism, the electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field in spacetime. The field tensor was first used after the four-dimensional tensor formulation of special relativity was introduced by Hermann Minkowski. The tensor allows related physical laws to be written very concisely.

In physics, deformation is the continuum mechanics transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body.
In continuum mechanics, an Arruda–Boyce model is a hyperelastic constitutive model used to describe the mechanical behavior of rubber and other polymeric substances. This model is based on the statistical mechanics of a material with a cubic representative volume element containing eight chains along the diagonal directions. The material is assumed to be incompressible. The model is named after Ellen Arruda and Mary Cunningham Boyce, who published it in 1993.
In statistics, the matrix t-distribution is the generalization of the multivariate t-distribution from vectors to matrices. The matrix t-distribution shares the same relationship with the multivariate t-distribution that the matrix normal distribution shares with the multivariate normal distribution. For example, the matrix t-distribution is the compound distribution that results from sampling from a matrix normal distribution having sampled the covariance matrix of the matrix normal from an inverse Wishart distribution.





















