In quantum mechanics, bra–ket notation, or Dirac notation, is ubiquitous. The notation uses the angle brackets, "" and "", and a vertical bar "", to construct "bras" and "kets".

In mathematics, an inner product space or a Hausdorff pre-Hilbert space is a vector space with a binary operation called an inner product. This operation associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors, often denoted using angle brackets. Inner products allow the rigorous introduction of intuitive geometrical notions, such as the length of a vector or the angle between two vectors. They also provide the means of defining orthogonality between vectors. Inner product spaces generalize Euclidean spaces to vector spaces of any dimension, and are studied in functional analysis. Inner product spaces over the field of complex numbers are sometimes referred to as unitary spaces. The first usage of the concept of a vector space with an inner product is due to Giuseppe Peano, in 1898.

In quantum mechanics, the uncertainty principle is any of a variety of mathematical inequalities asserting a fundamental limit to the accuracy with which the values for certain pairs of physical quantities of a particle, such as position, x, and momentum, p, can be predicted from initial conditions.

In mathematics, the Dirac delta function is a generalized function or distribution introduced by physicist Paul Dirac. It is called a function, although it is not a function on the level one would expect, that is, it is not a function R → C, but a function on the space of test functions. It is used to model the density of an idealized point mass or point charge as a function equal to zero everywhere except for zero and whose integral over the entire real line is equal to one. As there is no function that has these properties, the computations made by theoretical physicists appeared to mathematicians as nonsense until the introduction of distributions by Laurent Schwartz to formalize and validate the computations. As a distribution, the Dirac delta function is a linear functional that maps every function to its value at zero. The Kronecker delta function, which is usually defined on a discrete domain and takes values 0 and 1, is a discrete analog of the Dirac delta function.
A mathematical symbol is a figure or a combination of figures that is used to represent a mathematical object, an action on mathematical objects, a relation between mathematical objects, or for structuring the other symbols that occur in a formula. As formulas are entirely constituted with symbols of various types, many symbols are needed for expressing all mathematics.

In mathematics, an inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions. It is used most often to compare two numbers on the number line by their size. There are several different notations used to represent different kinds of inequalities:

In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the useful work obtainable from a closed thermodynamic system at a constant temperature (isothermal). The change in the Helmholtz energy during a process is equal to the maximum amount of work that the system can perform in a thermodynamic process in which temperature is held constant. At constant temperature, the Helmholtz free energy is minimized at equilibrium.
In quantum information theory, a quantum circuit is a model for quantum computation in which a computation is a sequence of quantum gates, which are reversible transformations on a quantum mechanical analog of an n-bit register. This analogous structure is referred to as an n-qubit register. The graphical depiction of quantum circuit elements is described using a variant of the Penrose graphical notation.

Euler–Bernoulli beam theory is a simplification of the linear theory of elasticity which provides a means of calculating the load-carrying and deflection characteristics of beams. It covers the case for small deflections of a beam that are subjected to lateral loads only. It is thus a special case of Timoshenko beam theory. It was first enunciated circa 1750, but was not applied on a large scale until the development of the Eiffel Tower and the Ferris wheel in the late 19th century. Following these successful demonstrations, it quickly became a cornerstone of engineering and an enabler of the Second Industrial Revolution.
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to generalize the derivative of a real-valued function of a single real variable to the case of a vector-valued function of multiple real variables, and to define the functional derivative used widely in the calculus of variations.

Emittance is a property of a charged particle beam in a particle accelerator. It is a measure for the average spread of particle coordinates in position-and-momentum phase space and has the dimension of length or length times angle. As a particle beam propagates along magnets and other beam-manipulating components of an accelerator, the position spread may change, but in a way that does not change the emittance. If the distribution over phase space is represented as a cloud in a plot, emittance is the area of the cloud. A more exact definition handles the fuzzy borders of the cloud and the case of a cloud that does not have an elliptical shape.
In mathematics, the Hamburger moment problem, named after Hans Ludwig Hamburger, is formulated as follows: given a sequence, does there exist a positive Borel measure μ on the real line such that

Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory.
In combinatorics, the Eulerian numberA(n, m) is the number of permutations of the numbers 1 to n in which exactly m elements are greater than the previous element. They are the coefficients of the Eulerian polynomials:
In probability theory, the Wick product is a particular way of defining an adjusted product of a set of random variables. In the lowest order product the adjustment corresponds to subtracting off the mean value, to leave a result whose mean is zero. For the higher order products the adjustment involves subtracting off lower order (ordinary) products of the random variables, in a symmetric way, again leaving a result whose mean is zero. The Wick product is a polynomial function of the random variables, their expected values, and expected values of their products.
In mathematics, brackets of various typographical forms, such as parentheses ( ), square brackets [ ], braces { } and angle brackets ⟨ ⟩, are frequently used in mathematical notation. Generally, such bracketing denotes some form of grouping: in evaluating an expression containing a bracketed sub-expression, the operators in the sub-expression take precedence over those surrounding it. Additionally, there are several uses and meanings for the various brackets.
Singularity functions are a class of discontinuous functions that contain singularities, i.e. they are discontinuous at their singular points. Singularity functions have been heavily studied in the field of mathematics under the alternative names of generalized functions and distribution theory. The functions are notated with brackets, as where n is an integer. The "" are often referred to as singularity brackets. The functions are defined as:
Macaulay’s method is a technique used in structural analysis to determine the deflection of Euler-Bernoulli beams. Use of Macaulay’s technique is very convenient for cases of discontinuous and/or discrete loading. Typically partial uniformly distributed loads (u.d.l.) and uniformly varying loads (u.v.l.) over the span and a number of concentrated loads are conveniently handled using this technique.
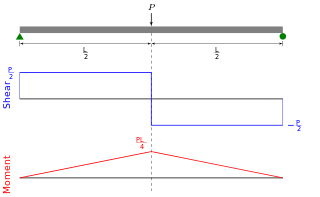
Shear and bending moment diagrams are analytical tools used in conjunction with structural analysis to help perform structural design by determining the value of shear force and bending moment at a given point of a structural element such as a beam. These diagrams can be used to easily determine the type, size, and material of a member in a structure so that a given set of loads can be supported without structural failure. Another application of shear and moment diagrams is that the deflection of a beam can be easily determined using either the moment area method or the conjugate beam method.
The partition function or configuration integral, as used in probability theory, information theory and dynamical systems, is a generalization of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann distribution. The partition function occurs in many problems of probability theory because, in situations where there is a natural symmetry, its associated probability measure, the Gibbs measure, has the Markov property. This means that the partition function occurs not only in physical systems with translation symmetry, but also in such varied settings as neural networks, and applications such as genomics, corpus linguistics and artificial intelligence, which employ Markov networks, and Markov logic networks. The Gibbs measure is also the unique measure that has the property of maximizing the entropy for a fixed expectation value of the energy; this underlies the appearance of the partition function in maximum entropy methods and the algorithms derived therefrom.

















