
Electrostatics is a branch of physics that studies slow-moving or stationary electric charges.

A polaron is a quasiparticle used in condensed matter physics to understand the interactions between electrons and atoms in a solid material. The polaron concept was proposed by Lev Landau in 1933 and Solomon Pekar in 1946 to describe an electron moving in a dielectric crystal where the atoms displace from their equilibrium positions to effectively screen the charge of an electron, known as a phonon cloud. This lowers the electron mobility and increases the electron's effective mass.
The DLVO theory explains the aggregation and kinetic stability of aqueous dispersions quantitatively and describes the force between charged surfaces interacting through a liquid medium. It combines the effects of the van der Waals attraction and the electrostatic repulsion due to the so-called double layer of counterions. The electrostatic part of the DLVO interaction is computed in the mean field approximation in the limit of low surface potentials - that is when the potential energy of an elementary charge on the surface is much smaller than the thermal energy scale, . For two spheres of radius each having a charge separated by a center-to-center distance in a fluid of dielectric constant containing a concentration of monovalent ions, the electrostatic potential takes the form of a screened-Coulomb or Yukawa potential,
A multipole expansion is a mathematical series representing a function that depends on angles—usually the two angles used in the spherical coordinate system for three-dimensional Euclidean space, . Similarly to Taylor series, multipole expansions are useful because oftentimes only the first few terms are needed to provide a good approximation of the original function. The function being expanded may be real- or complex-valued and is defined either on , or less often on for some other .
Jellium, also known as the uniform electron gas (UEG) or homogeneous electron gas (HEG), is a quantum mechanical model of interacting electrons in a solid where the positive charges are assumed to be uniformly distributed in space; the electron density is a uniform quantity as well in space. This model allows one to focus on the effects in solids that occur due to the quantum nature of electrons and their mutual repulsive interactions without explicit introduction of the atomic lattice and structure making up a real material. Jellium is often used in solid-state physics as a simple model of delocalized electrons in a metal, where it can qualitatively reproduce features of real metals such as screening, plasmons, Wigner crystallization and Friedel oscillations.
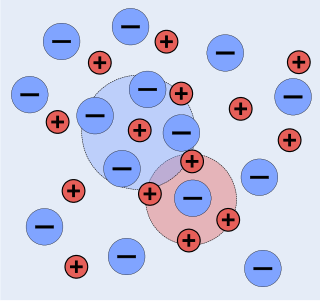
The chemists Peter Debye and Erich Hückel noticed that solutions that contain ionic solutes do not behave ideally even at very low concentrations. So, while the concentration of the solutes is fundamental to the calculation of the dynamics of a solution, they theorized that an extra factor that they termed gamma is necessary to the calculation of the activities of the solution. Hence they developed the Debye–Hückel equation and Debye–Hückel limiting law. The activity is only proportional to the concentration and is altered by a factor known as the activity coefficient . This factor takes into account the interaction energy of ions in solution.
Surface states are electronic states found at the surface of materials. They are formed due to the sharp transition from solid material that ends with a surface and are found only at the atom layers closest to the surface. The termination of a material with a surface leads to a change of the electronic band structure from the bulk material to the vacuum. In the weakened potential at the surface, new electronic states can be formed, so called surface states.
In chemistry, the lattice energy is the energy change upon formation of one mole of a crystalline ionic compound from its constituent ions, which are assumed to initially be in the gaseous state. It is a measure of the cohesive forces that bind ionic solids. The size of the lattice energy is connected to many other physical properties including solubility, hardness, and volatility. Since it generally cannot be measured directly, the lattice energy is usually deduced from experimental data via the Born–Haber cycle.
Ewald summation, named after Paul Peter Ewald, is a method for computing long-range interactions in periodic systems. It was first developed as the method for calculating the electrostatic energies of ionic crystals, and is now commonly used for calculating long-range interactions in computational chemistry. Ewald summation is a special case of the Poisson summation formula, replacing the summation of interaction energies in real space with an equivalent summation in Fourier space. In this method, the long-range interaction is divided into two parts: a short-range contribution, and a long-range contribution which does not have a singularity. The short-range contribution is calculated in real space, whereas the long-range contribution is calculated using a Fourier transform. The advantage of this method is the rapid convergence of the energy compared with that of a direct summation. This means that the method has high accuracy and reasonable speed when computing long-range interactions, and it is thus the de facto standard method for calculating long-range interactions in periodic systems. The method requires charge neutrality of the molecular system to accurately calculate the total Coulombic interaction. A study of the truncation errors introduced in the energy and force calculations of disordered point-charge systems is provided by Kolafa and Perram.
In condensed matter physics and crystallography, the static structure factor is a mathematical description of how a material scatters incident radiation. The structure factor is a critical tool in the interpretation of scattering patterns obtained in X-ray, electron and neutron diffraction experiments.

In condensed-matter physics, channelling (or channeling) is the process that constrains the path of a charged particle in a crystalline solid.
In statistical mechanics, the two-dimensional square lattice Ising model is a simple lattice model of interacting magnetic spins. The model is notable for having nontrivial interactions, yet having an analytical solution. The model was solved by Lars Onsager for the special case that the external magnetic field H = 0. An analytical solution for the general case for has yet to be found.
The Poisson–Boltzmann equation is a useful equation in many settings, whether it be to understand physiological interfaces, polymer science, electron interactions in a semiconductor, or more. It aims to describe the distribution of the electric potential in solution in the direction normal to a charged surface. This distribution is important to determine how the electrostatic interactions will affect the molecules in solution. The Poisson–Boltzmann equation is derived via mean-field assumptions. From the Poisson–Boltzmann equation many other equations have been derived with a number of different assumptions.
The Debye–Hückel theory was proposed by Peter Debye and Erich Hückel as a theoretical explanation for departures from ideality in solutions of electrolytes and plasmas. It is a linearized Poisson–Boltzmann model, which assumes an extremely simplified model of electrolyte solution but nevertheless gave accurate predictions of mean activity coefficients for ions in dilute solution. The Debye–Hückel equation provides a starting point for modern treatments of non-ideality of electrolyte solutions.
The Kapustinskii equation calculates the lattice energy UL for an ionic crystal, which is experimentally difficult to determine. It is named after Anatoli Fedorovich Kapustinskii who published the formula in 1956.
The Born–Landé equation is a means of calculating the lattice energy of a crystalline ionic compound. In 1918 Max Born and Alfred Landé proposed that the lattice energy could be derived from the electrostatic potential of the ionic lattice and a repulsive potential energy term.
The isotopic shift is the shift in various forms of spectroscopy that occurs when one nuclear isotope is replaced by another.

The electric dipole moment is a measure of the separation of positive and negative electrical charges within a system, that is, a measure of the system's overall polarity. The SI unit for electric dipole moment is the coulomb-meter (C⋅m). The debye (D) is another unit of measurement used in atomic physics and chemistry.

Double layer forces occur between charged objects across liquids, typically water. This force acts over distances that are comparable to the Debye length, which is on the order of one to a few tenths of nanometers. The strength of these forces increases with the magnitude of the surface charge density. For two similarly charged objects, this force is repulsive and decays exponentially at larger distances, see figure. For unequally charged objects and eventually at shorted distances, these forces may also be attractive. The theory due to Derjaguin, Landau, Verwey, and Overbeek (DLVO) combines such double layer forces together with Van der Waals forces in order to estimate the actual interaction potential between colloidal particles.
The Born–Mayer equation is an equation that is used to calculate the lattice energy of a crystalline ionic compound. It is a refinement of the Born–Landé equation by using an improved repulsion term.




















