In geometry, a dodecahedron or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120.

In geometry, a hexagon is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.

In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.

A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.

In geometry, a dodecagon, or 12-gon, is any twelve-sided polygon.
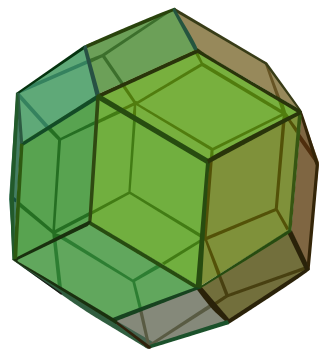
In geometry, the rhombic triacontahedron, sometimes simply called the triacontahedron as it is the most common thirty-faced polyhedron, is a convex polyhedron with 30 rhombic faces. It has 60 edges and 32 vertices of two types. It is a Catalan solid, and the dual polyhedron of the icosidodecahedron. It is a zonohedron.

Cuisenaire rods are mathematics learning aids for students that provide an interactive, hands-on way to explore mathematics and learn mathematical concepts, such as the four basic arithmetical operations, working with fractions and finding divisors. In the early 1950s, Caleb Gattegno popularised this set of coloured number rods created by Georges Cuisenaire (1891–1975), a Belgian primary school teacher, who called the rods réglettes.

In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which exactly three hexagons meet at each vertex. It has Schläfli symbol of {6,3} or t{3,6} .

In geometry, the triangular tiling or triangular tessellation is one of the three regular tilings of the Euclidean plane, and is the only such tiling where the constituent shapes are not parallelogons. Because the internal angle of the equilateral triangle is 60 degrees, six triangles at a point occupy a full 360 degrees. The triangular tiling has Schläfli symbol of {3,6}.

In geometry, the truncated hexagonal tiling is a semiregular tiling of the Euclidean plane. There are 2 dodecagons (12-sides) and one triangle on each vertex.

In geometry, the rhombitrihexagonal tiling is a semiregular tiling of the Euclidean plane. There are one triangle, two squares, and one hexagon on each vertex. It has Schläfli symbol of rr{3,6}.

In geometry, the rhombille tiling, also known as tumbling blocks, reversible cubes, or the dice lattice, is a tessellation of identical 60° rhombi on the Euclidean plane. Each rhombus has two 60° and two 120° angles; rhombi with this shape are sometimes also called diamonds. Sets of three rhombi meet at their 120° angles, and sets of six rhombi meet at their 60° angles.

In geometry, the trapezo-rhombic dodecahedron or rhombo-trapezoidal dodecahedron is a convex dodecahedron with 6 rhombic and 6 trapezoidal faces. It has D3h symmetry. A concave form can be constructed with an identical net, seen as excavating trigonal trapezohedra from the top and bottom. It is also called the trapezoidal dodecahedron.
In geometry, a near-miss Johnson solid is a strictly convex polyhedron whose faces are close to being regular polygons but some or all of which are not precisely regular. Thus, it fails to meet the definition of a Johnson solid, a polyhedron whose faces are all regular, though it "can often be physically constructed without noticing the discrepancy" between its regular and irregular faces. The precise number of near-misses depends on how closely the faces of such a polyhedron are required to approximate regular polygons.

Pattern Blocks are a set of mathematical manipulatives developed in the 1960s. The six shapes are both a play resource and a tool for learning in mathematics, which serve to develop spatial reasoning skills that are fundamental to the learning of mathematics. Among other things, they allow children to see how shapes can be composed and decomposed into other shapes, and introduce children to ideas of tilings. Pattern blocks sets are multiple copies of just six shapes:

In geometry, an octadecagon or 18-gon is an eighteen-sided polygon.

Virtual math manipulatives are visual representations of concrete math manipulatives. They are digitally accessed through a variety of websites and apps, as well as through tablets, phones and computers. Virtual math manipulatives are modeled after concrete math manipulatives that are commonly used in classrooms to physically represent mathematical concepts and support student understanding of mathematical concepts.

Montessori sensorial materials are materials used in the Montessori classroom to help a child develop and refine their five senses. Use of these materials constitutes the next level of difficulty after those of practical life.

In the geometry of tessellations, a rep-tile or reptile is a shape that can be dissected into smaller copies of the same shape. The term was coined as a pun on animal reptiles by recreational mathematician Solomon W. Golomb and popularized by Martin Gardner in his "Mathematical Games" column in the May 1963 issue of Scientific American. In 2012 a generalization of rep-tiles called self-tiling tile sets was introduced by Lee Sallows in Mathematics Magazine.





















