In probability theory and statistics, kurtosis is a measure of the "tailedness" of the probability distribution of a real-valued random variable. In a similar way to the concept of skewness, kurtosis is a descriptor of the shape of a probability distribution and, just as for skewness, there are different ways of quantifying it for a theoretical distribution and corresponding ways of estimating it from a sample from a population. Depending on the particular measure of kurtosis that is used, there are various interpretations of kurtosis, and of how particular measures should be interpreted.
In probability theory and statistics, a central moment is a moment of a probability distribution of a random variable about the random variable's mean; that is, it is the expected value of a specified integer power of the deviation of the random variable from the mean. The various moments form one set of values by which the properties of a probability distribution can be usefully characterized. Central moments are used in preference to ordinary moments, computed in terms of deviations from the mean instead of from zero, because the higher-order central moments relate only to the spread and shape of the distribution, rather than also to its location.

In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive or negative, or undefined.
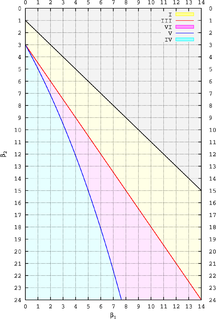
The Pearson distribution is a family of continuous probability distributions. It was first published by Karl Pearson in 1895 and subsequently extended by him in 1901 and 1916 in a series of articles on biostatistics.
In probability theory, the Gillespie algorithm generates a statistically correct trajectory of a stochastic equation. It was created by Joseph L. Doob and others, presented by Dan Gillespie in 1976, and popularized in 1977 in a paper where he uses it to simulate chemical or biochemical systems of reactions efficiently and accurately using limited computational power. As computers have become faster, the algorithm has been used to simulate increasingly complex systems. The algorithm is particularly useful for simulating reactions within cells, where the number of reagents is low and keeping track of the position and behaviour of individual molecules is computationally feasible. Mathematically, it is a variant of a dynamic Monte Carlo method and similar to the kinetic Monte Carlo methods. It is used heavily in computational systems biology.
A stochastic simulation is a simulation that traces the evolution of variables that can change stochastically (randomly) with certain probabilities.
In probability and statistics, the Tweedie distributions are a family of probability distributions which include the purely continuous normal and gamma distributions, the purely discrete scaled Poisson distribution, and the class of mixed compound Poisson–gamma distributions which have positive mass at zero, but are otherwise continuous. For any random variable Y that obeys a Tweedie distribution, the variance var(Y) relates to the mean E(Y) by the power law,
This page lists articles related to probability theory. In particular, it lists many articles corresponding to specific probability distributions. Such articles are marked here by a code of the form (X:Y), which refers to number of random variables involved and the type of the distribution. For example (2:DC) indicates a distribution with two random variables, discrete or continuous. Other codes are just abbreviations for topics. The list of codes can be found in the table of contents.
In statistics, L-moments are a sequence of statistics used to summarize the shape of a probability distribution. They are linear combinations of order statistics (L-statistics) analogous to conventional moments, and can be used to calculate quantities analogous to standard deviation, skewness and kurtosis, termed the L-scale, L-skewness and L-kurtosis respectively. Standardised L-moments are called L-moment ratios and are analogous to standardized moments. Just as for conventional moments, a theoretical distribution has a set of population L-moments. Sample L-moments can be defined for a sample from the population, and can be used as estimators of the population L-moments.
In statistics, the Jarque–Bera test is a goodness-of-fit test of whether sample data have the skewness and kurtosis matching a normal distribution. The test is named after Carlos Jarque and Anil K. Bera. The test statistic is always nonnegative. If it is far from zero, it signals the data do not have a normal distribution.
John Gordon Skellam (1914-1979) was a statistician and ecologist, who discovered the Skellam distribution.
In queueing theory, a discipline within the mathematical theory of probability, an M/G/1 queue is a queue model where arrivals are Markovian, service times have a General distribution and there is a single server. The model name is written in Kendall's notation, and is an extension of the M/M/1 queue, where service times must be exponentially distributed. The classic application of the M/G/1 queue is to model performance of a fixed head hard disk.
In queueing theory, a discipline within the mathematical theory of probability, an M/G/k queue is a queue model where arrivals are Markovian, service times have a General distribution and there are k servers. The model name is written in Kendall's notation, and is an extension of the M/M/c queue, where service times must be exponentially distributed and of the M/G/1 queue with a single server. Most performance metrics for this queueing system are not known and remain an open problem.
In probability theory, a piecewise-deterministic Markov process (PDMP) is a process whose behaviour is governed by random jumps at points in time, but whose evolution is deterministically governed by an ordinary differential equation between those times. The class of models is "wide enough to include as special cases virtually all the non-diffusion models of applied probability." The process is defined by three quantities: the flow, the jump rate, and the transition measure.
In queueing theory, a discipline within the mathematical theory of probability, the G/G/1 queue represents the queue length in a system with a single server where interarrival times have a general distribution and service times have a (different) general distribution. The evolution of the queue can be described by the Lindley equation.