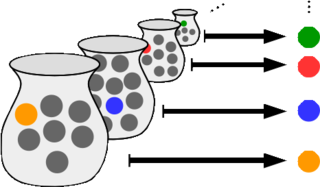
In mathematics, the axiom of choice, or AC, is an axiom of set theory equivalent to the statement that a Cartesian product of a collection of non-empty sets is non-empty. Informally put, the axiom of choice says that given any collection of bins, each containing at least one object, it is possible to make a selection of exactly one object from each bin, even if the collection is infinite. Formally, it states that for every indexed family of nonempty sets there exists an indexed family of elements such that for every . The axiom of choice was formulated in 1904 by Ernst Zermelo in order to formalize his proof of the well-ordering theorem.
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and an end in obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics and from evolutionary biology to computer science.
Computational complexity theory focuses on classifying computational problems according to their resource usage, and relating these classes to each other. A computational problem is a task solved by a computer. A computation problem is solvable by mechanical application of mathematical steps, such as an algorithm.

Discrete mathematics is the study of mathematical structures that can be considered "discrete" rather than "continuous". Objects studied in discrete mathematics include integers, graphs, and statements in logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets. However, there is no exact definition of the term "discrete mathematics".
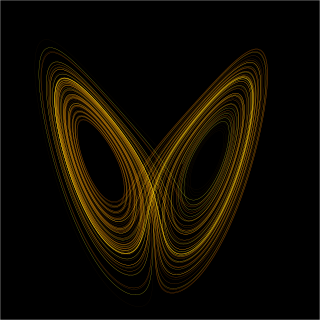
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it.

A cellular automaton is a discrete model of computation studied in automata theory. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessellation structures, and iterative arrays. Cellular automata have found application in various areas, including physics, theoretical biology and microstructure modeling.

In quantum mechanics, a probability amplitude is a complex number used in describing the behaviour of systems. The modulus squared of this quantity represents a probability density.

In the mathematical field of graph theory, a spanning treeT of an undirected graph G is a subgraph that is a tree which includes all of the vertices of G. In general, a graph may have several spanning trees, but a graph that is not connected will not contain a spanning tree. If all of the edges of G are also edges of a spanning tree T of G, then G is a tree and is identical to T.
A hybrid system is a dynamical system that exhibits both continuous and discrete dynamic behavior – a system that can both flow and jump. Often, the term "hybrid dynamical system" is used, to distinguish over hybrid systems such as those that combine neural nets and fuzzy logic, or electrical and mechanical drivelines. A hybrid system has the benefit of encompassing a larger class of systems within its structure, allowing for more flexibility in modeling dynamic phenomena.

Dynamical systems theory is an area of mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. From a physical point of view, continuous dynamical systems is a generalization of classical mechanics, a generalization where the equations of motion are postulated directly and are not constrained to be Euler–Lagrange equations of a least action principle. When difference equations are employed, the theory is called discrete dynamical systems. When the time variable runs over a set that is discrete over some intervals and continuous over other intervals or is any arbitrary time-set such as a Cantor set, one gets dynamic equations on time scales. Some situations may also be modeled by mixed operators, such as differential-difference equations.

In a cellular automaton, a Garden of Eden is a configuration that has no predecessor. It can be the initial configuration of the automaton but cannot arise in any other way. John Tukey named these configurations after the Garden of Eden in Abrahamic religions, which was created out of nowhere.
In mathematics, symbolic dynamics is the practice of modeling a topological or smooth dynamical system by a discrete space consisting of infinite sequences of abstract symbols, each of which corresponds to a state of the system, with the dynamics (evolution) given by the shift operator. Formally, a Markov partition is used to provide a finite cover for the smooth system; each set of the cover is associated with a single symbol, and the sequences of symbols result as a trajectory of the system moves from one covering set to another.
In mathematics, subshifts of finite type are used to model dynamical systems, and in particular are the objects of study in symbolic dynamics and ergodic theory. They also describe the set of all possible sequences executed by a finite state machine. The most widely studied shift spaces are the subshifts of finite type.
Motion planning, also path planning is a computational problem to find a sequence of valid configurations that moves the object from the source to destination. The term is used in computational geometry, computer animation, robotics and computer games.
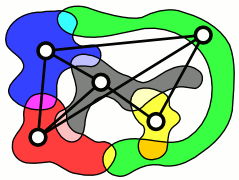
In graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph can be represented as an intersection graph, but some important special classes of graphs can be defined by the types of sets that are used to form an intersection representation of them.
A topological game is an infinite game of perfect information played between two players on a topological space. Players choose objects with topological properties such as points, open sets, closed sets and open coverings. Time is generally discrete, but the plays may have transfinite lengths, and extensions to continuum time have been put forth. The conditions for a player to win can involve notions like topological closure and convergence.
The Curtis–Hedlund–Lyndon theorem is a mathematical characterization of cellular automata in terms of their symbolic dynamics. It is named after Morton L. Curtis, Gustav A. Hedlund, and Roger Lyndon; in his 1969 paper stating the theorem, Hedlund credited Curtis and Lyndon as co-discoverers. It has been called "one of the fundamental results in symbolic dynamics".
In mathematics, the concept of graph dynamical systems can be used to capture a wide range of processes taking place on graphs or networks. A major theme in the mathematical and computational analysis of GDSs is to relate their structural properties and the global dynamics that result.

A reversible cellular automaton is a cellular automaton in which every configuration has a unique predecessor. That is, it is a regular grid of cells, each containing a state drawn from a finite set of states, with a rule for updating all cells simultaneously based on the states of their neighbors, such that the previous state of any cell before an update can be determined uniquely from the updated states of all the cells. The time-reversed dynamics of a reversible cellular automaton can always be described by another cellular automaton rule, possibly on a much larger neighborhood.
In mathematical dynamics, discrete time and continuous time are two alternative frameworks within which to model variables that evolve over time.











