
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point is called the pole, and the ray from the pole in the reference direction is the polar axis. The distance from the pole is called the radial coordinate, radial distance or simply radius, and the angle is called the angular coordinate, polar angle, or azimuth. The radial coordinate is often denoted by r or ρ, and the angular coordinate by φ, θ, or t. Angles in polar notation are generally expressed in either degrees or radians.

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is said to be a tangent of a curve y = f(x) at a point x = c if the line passes through the point (c, f ) on the curve and has slope f'(c), where f' is the derivative of f. A similar definition applies to space curves and curves in n-dimensional Euclidean space.

In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function.
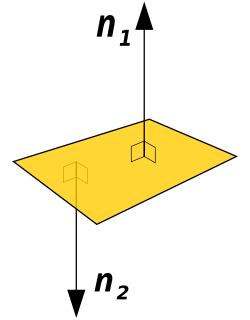
In geometry, a normal is an object such as a line, ray, or vector that is perpendicular to a given object. For example, in two dimensions, the normal line to a curve at a given point is the line perpendicular to the tangent line to the curve at the point. A normal vector may have length one or its length may represent the curvature of the object ; its algebraic sign may indicate sides.

In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation h(x, y, t) = 0 can be restricted to the affine algebraic plane curve of equation h(x, y, 1) = 0. These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered.
In the calculus of variations, the Euler equation is a second-order partial differential equation whose solutions are the functions for which a given functional is stationary. It was developed by Swiss mathematician Leonhard Euler and Italian mathematician Joseph-Louis Lagrange in the 1750s.
In mathematics, Frobenius' theorem gives necessary and sufficient conditions for finding a maximal set of independent solutions of an underdetermined system of first-order homogeneous linear partial differential equations. In modern geometric terms, given a family of vector fields, the theorem gives necessary and sufficient integrability conditions for the existence of a foliation by maximal integral manifolds whose tangent bundles are spanned by the given vector fields. The theorem generalizes the existence theorem for ordinary differential equations, which guarantees that a single vector field always gives rise to integral curves; Frobenius gives compatibility conditions under which the integral curves of r vector fields mesh into coordinate grids on r-dimensional integral manifolds. The theorem is foundational in differential topology and calculus on manifolds.

A cardioid is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal spiral, and an inverse curve of the parabola with the focus as the center of inversion. It's also the set of points of reflections of a fixed point on a circle through all tangents to the circle.

In mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation. The method is to reduce a partial differential equation to a family of ordinary differential equations along which the solution can be integrated from some initial data given on a suitable hypersurface.
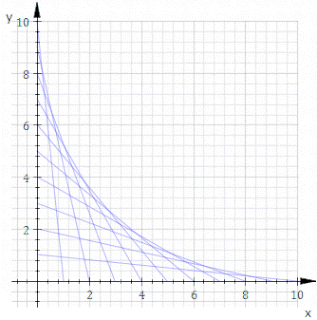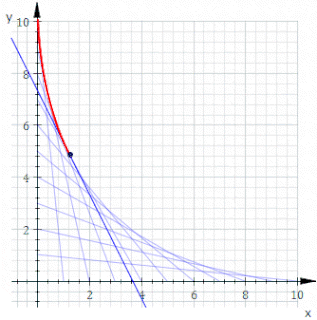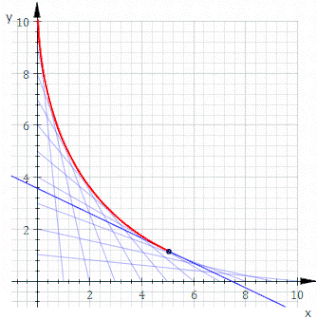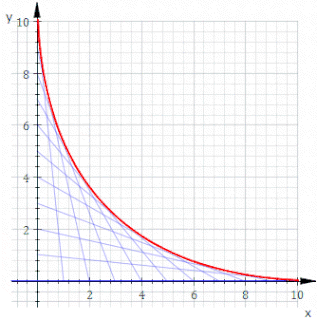
In geometry, an envelope of a planar family of curves is a curve that is tangent to each member of the family at some point, and these points of tangency together form the whole envelope. Classically, a point on the envelope can be thought of as the intersection of two "infinitesimally adjacent" curves, meaning the limit of intersections of nearby curves. This idea can be generalized to an envelope of surfaces in space, and so on to higher dimensions.

In projective geometry, a dual curve of a given plane curve C is a curve in the dual projective plane consisting of the set of lines tangent to C. There is a map from a curve to its dual, sending each point to the point dual to its tangent line. If C is algebraic then so is its dual and the degree of the dual is known as the class of the original curve. The equation of the dual of C, given in line coordinates, is known as the tangential equation of C.

In mathematics, a surface is a generalization of a plane, which is not necessarily flat – that is, the curvature is not necessarily zero. This is analogous to a curve generalizing a straight line. There are many more precise definitions, depending on the context and the mathematical tools that are used to analyze the surface.
In mathematics, a first-order partial differential equation is a partial differential equation that involves only first derivatives of the unknown function of n variables. The equation takes the form
In mathematics, a (real) Monge–Ampère equation is a nonlinear second-order partial differential equation of special kind. A second-order equation for the unknown function u of two variables x,y is of Monge–Ampère type if it is linear in the determinant of the Hessian matrix of u and in the second-order partial derivatives of u. The independent variables (x,y) vary over a given domain D of R2. The term also applies to analogous equations with n independent variables. The most complete results so far have been obtained when the equation is elliptic.

In algebraic geometry, the first polar, or simply polar of an algebraic plane curve C of degree n with respect to a point Q is an algebraic curve of degree n−1 which contains every point of C whose tangent line passes through Q. It is used to investigate the relationship between the curve and its dual, for example in the derivation of the Plücker formulas.

In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss, who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.
In the mathematical theory of partial differential equations, a Monge equation, named after Gaspard Monge, is a first-order partial differential equation for an unknown function u in the independent variables x1,...,xn

In mathematics, a conic section is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.
For a plane curve C and a given fixed point O, the pedal equation of the curve is a relation between r and p where r is the distance from O to a point on C and p is the perpendicular distance from O to the tangent line to C at the point. The point O is called the pedal point and the values r and p are sometimes called the pedal coordinates of a point relative to the curve and the pedal point. It is also useful to measure the distance of O to the normal even though it is not an independent quantity and it relates to as .

In geometry, an intersection is a point, line, or curve common to two or more objects. The simplest case in Euclidean geometry is the intersection of two distinct lines, which either is one point or does not exist if the lines are parallel.

























