Papyrus is a material similar to thick paper that was used in ancient times as a writing surface. It was made from the pith of the papyrus plant, Cyperus papyrus, a wetland sedge. Papyrus can also refer to a document written on sheets of such material, joined side by side and rolled up into a scroll, an early form of a book.

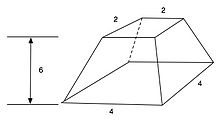
In geometry, a frustum ; is the portion of a solid that lies between two parallel planes cutting this solid. In the case of a pyramid, the base faces are polygonal and the side faces are trapezoidal. A right frustum is a right pyramid or a right cone truncated perpendicularly to its axis; otherwise, it is an oblique frustum.

In geometry, an isosceles triangle is a triangle that has two sides of equal length. Sometimes it is specified as having exactly two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case. Examples of isosceles triangles include the isosceles right triangle, the golden triangle, and the faces of bipyramids and certain Catalan solids.

An Egyptian fraction is a finite sum of distinct unit fractions, such as
The system of ancient Egyptian numerals was used in Ancient Egypt from around 3000 BCE until the early first millennium CE. It was a system of numeration based on multiples of ten, often rounded off to the higher power, written in hieroglyphs. The Egyptians had no concept of a positional notation such as the decimal system. The hieratic form of numerals stressed an exact finite series notation, ciphered one-to-one onto the Egyptian alphabet.
Ancient Egyptian mathematics is the mathematics that was developed and used in Ancient Egypt c. 3000 to c. 300 BCE, from the Old Kingdom of Egypt until roughly the beginning of Hellenistic Egypt. The ancient Egyptians utilized a numeral system for counting and solving written mathematical problems, often involving multiplication and fractions. Evidence for Egyptian mathematics is limited to a scarce amount of surviving sources written on papyrus. From these texts it is known that ancient Egyptians understood concepts of geometry, such as determining the surface area and volume of three-dimensional shapes useful for architectural engineering, and algebra, such as the false position method and quadratic equations.
In mathematics, ancient Egyptian multiplication, one of two multiplication methods used by scribes, is a systematic method for multiplying two numbers that does not require the multiplication table, only the ability to multiply and divide by 2, and to add. It decomposes one of the multiplicands into a set of numbers of powers of two and then creates a table of doublings of the second multiplicand by every value of the set which is summed up to give result of multiplication.
In mathematics, the Heronian meanH of two non-negative real numbers A and B is given by the formula
The Egyptian Mathematical Leather Roll (EMLR) is a 10 × 17 in (25 × 43 cm) leather roll purchased by Alexander Henry Rhind in 1858. It was sent to the British Museum in 1864, along with the Rhind Mathematical Papyrus, but it was not chemically softened and unrolled until 1927 (Scott, Hall 1927).
The Reisner Papyri date to the reign of Senusret I, who was king of ancient Egypt in the 19th century BCE. The documents were discovered by G.A. Reisner during excavations in 1901–04 in Naga ed-Deir in southern Egypt. A total of four papyrus rolls were found in a wooden coffin in a tomb.
The hekat or heqat was an ancient Egyptian volume unit used to measure grain, bread, and beer. It equals 4.8 litres, or about 1.056 imperial gallons, in today's measurements.

The Rhind Mathematical Papyrus is one of the best known examples of ancient Egyptian mathematics. It is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1550 BC. The British Museum, where the majority of the papyrus is now kept, acquired it in 1865 along with the Egyptian Mathematical Leather Roll, also owned by Henry Rhind. There are a few small fragments held by the Brooklyn Museum in New York City and an 18 cm (7.1 in) central section is missing. It is one of the two well-known Mathematical Papyri along with the Moscow Mathematical Papyrus. The Rhind Papyrus is larger than the Moscow Mathematical Papyrus, while the latter is older.
The Rhind Mathematical Papyrus, an ancient Egyptian mathematical work, includes a mathematical table for converting rational numbers of the form 2/n into Egyptian fractions, the form the Egyptians used to write fractional numbers. The text describes the representation of 50 rational numbers. It was written during the Second Intermediate Period of Egypt by Ahmes, the first writer of mathematics whose name is known. Aspects of the document may have been copied from an unknown 1850 BCE text.
A timeline of algebra and geometry

Seked is an ancient Egyptian term describing the inclination of the triangular faces of a right pyramid. The system was based on the Egyptians' length measure known as the royal cubit. It was subdivided into seven palms, each of which was sub-divided into four digits. The inclination of measured slopes was therefore expressed as the number of horizontal palms and digits relative to each royal cubit rise.
The Lahun Mathematical Papyri is an ancient Egyptian mathematical text. It forms part of the Kahun Papyri, which was discovered at El-Lahun by Flinders Petrie during excavations of a workers' town near the pyramid of the 12th dynasty pharaoh Sesostris II. The Kahun Papyri are a collection of texts including administrative texts, medical texts, veterinarian texts and six fragments devoted to mathematics.

Egyptian geometry refers to geometry as it was developed and used in Ancient Egypt. Their geometry was a necessary outgrowth of surveying to preserve the layout and ownership of farmland, which was flooded annually by the Nile river.
In the history of mathematics, Egyptian algebra, as that term is used in this article, refers to algebra as it was developed and used in ancient Egypt. Ancient Egyptian mathematics as discussed here spans a time period ranging from c. 3000 BCE to c. 300 BCE.

Mathematics in Ancient Egypt: A Contextual History is a book on ancient Egyptian mathematics by Annette Imhausen. It was published by the Princeton University Press in 2016.