Nose cone design

Last updated January 23, 2024

Given the problem of the aerodynamic design of the nose cone section of any vehicle or body meant to travel through a compressible fluid medium (such as a rocket or aircraft, missile, shell or bullet), an important problem is the determination of the nose cone geometrical shape for optimum performance. For many applications, such a task requires the definition of a solid of revolution shape that experiences minimal resistance to rapid motion through such a fluid medium.

Nose cone shapes and equations

General dimensions

In all of the following nose cone shape equations, $L$ is the overall length of the nose cone and $R$ is the radius of the base of the nose cone. $y$ is the radius at any point $x$ , as $x$ varies from $0$ , at the tip of the nose cone, to $L$ . The equations define the two-dimensional profile of the nose shape. The full body of revolution of the nose cone is formed by rotating the profile around the centerline $C$ ⁄ $L$ . While the equations describe the 'perfect' shape, practical nose cones are often blunted or truncated for manufacturing, aerodynamic, or thermodynamic reasons.^[1]

Conic

Conic nose cone render and profile with parameters shown.

A very common nose-cone shape is a simple cone. This shape is often chosen for its ease of manufacture. More optimal, streamlined shapes (described below) are often much more difficult to create. The sides of a conic profile are straight lines, so the diameter equation is simply:

y={xR \over L}

Cones are sometimes defined by their half angle, $φ$ :

\phi =\arctan \left({R \over L}\right)

and

y=x\tan(\phi )\;

Spherically blunted conic

Spherically blunted conic nose cone render and profile with parameters shown.

In practical applications such as re-entry vehicles, a conical nose is often blunted by capping it with a segment of a sphere. The tangency point where the sphere meets the cone can be found from:

x_{t}={\frac {L^{2}}{R}}{\sqrt {\frac {r_{n}^{2}}{R^{2}+L^{2}}}}

y_{t}={\frac {x_{t}R}{L}}

where $r n$ is the radius of the spherical nose cap.

The center of the spherical nose cap, $x o$ , can be found from:

x_{o}=x_{t}+{\sqrt {r_{n}^{2}-y_{t}^{2}}}

And the apex point, $x a$ can be found from:

x_{a}=x_{o}-r_{n}

Bi-conic

Bi-conic nose cone render and profile with parameters shown.

A bi-conic nose cone shape is simply a cone with length $L 1$ stacked on top of a frustum of a cone (commonly known as a conical transition section shape) with length $L 2$ , where the base of the upper cone is equal in radius $R 1$ to the top radius of the smaller frustum with base radius $R 2$ .

L=L_{1}+L_{2}

For

0\leq x\leq L_{1}

:

y={xR_{1} \over L_{1}}

For

L_{1}\leq x\leq L

:

y=R_{1}+{(x-L_{1})(R_{2}-R_{1}) \over L_{2}}

Half angles:

\phi _{1}=\arctan \left({R_{1} \over L_{1}}\right)

and

y=x\tan(\phi _{1})\;

\phi _{2}=\arctan \left({R_{2}-R_{1} \over L_{2}}\right)

and

y=R_{1}+(x-L_{1})\tan(\phi _{2})\;

Tangent ogive

Tangent ogive nose cone render and profile with parameters and ogive circle shown.

Next to a simple cone, the tangent ogive shape is the most familiar in hobby rocketry. The profile of this shape is formed by a segment of a circle such that the rocket body is tangent to the curve of the nose cone at its base, and the base is on the radius of the circle. The popularity of this shape is largely due to the ease of constructing its profile, as it is simply a circular section.

The radius of the circle that forms the ogive is called the ogive radius, $ρ$ , and it is related to the length and base radius of the nose cone as expressed by the formula:

\rho ={R^{2}+L^{2} \over 2R}

The radius $y$ at any point $x$ , as $x$ varies from $0$ to $L$ is:

y={\sqrt {\rho ^{2}-(L-x)^{2}}}+R-\rho

The nose cone length, $L$ , must be less than or equal to $ρ$ . If they are equal, then the shape is a hemisphere.

Spherically blunted tangent ogive

Spherically blunted tangent ogive nose cone render and profile with parameters shown.

A tangent ogive nose is often blunted by capping it with a segment of a sphere. The tangency point where the sphere meets the tangent ogive can be found from:

{\begin{aligned}x_{o}&=L-{\sqrt {\left(\rho -r_{n}\right)^{2}-(\rho -R)^{2}}}\\y_{t}&={\frac {r_{n}(\rho -R)}{\rho -r_{n}}}\\x_{t}&=x_{o}-{\sqrt {r_{n}^{2}-y_{t}^{2}}}\end{aligned}}

where $r n$ is the radius and $x o$ is the center of the spherical nose cap.

Finally, the apex point can be found from:

x_{a}=x_{o}-r_{n}

Secant ogive

Secant ogive nose cone render and profile with parameters and ogive circle shown.

Alternate secant ogive render and profile which show a bulge due to a smaller radius.

The profile of this shape is also formed by a segment of a circle, but the base of the shape is not on the radius of the circle defined by the ogive radius. The rocket body will not be tangent to the curve of the nose at its base. The ogive radius $ρ$ is not determined by $R$ and $L$ (as it is for a tangent ogive), but rather is one of the factors to be chosen to define the nose shape. If the chosen ogive radius of a secant ogive is greater than the ogive radius of a tangent ogive with the same $R$ and $L$ , then the resulting secant ogive appears as a tangent ogive with a portion of the base truncated.

\rho >{R^{2}+L^{2} \over 2R}

and

\alpha =\arccos \left({{\sqrt {L^{2}+R^{2}}} \over 2\rho }\right)-\arctan \left({R \over L}\right)

Then the radius $y$ at any point $x$ as $x$ varies from $0$ to $L$ is:

y={\sqrt {\rho ^{2}-(\rho \cos(\alpha )-x)^{2}}}-\rho \sin(\alpha )

If the chosen $ρ$ is less than the tangent ogive $ρ$ and greater than half the length of the nose cone, then the result will be a secant ogive that bulges out to a maximum diameter that is greater than the base diameter. The classic example of this shape is the nose cone of the Honest John.

{\frac {L}{2}}<\rho <{R^{2}+L^{2} \over 2R}

Elliptical

Elliptical nose cone render and profile with parameters shown.

The profile of this shape is one-half of an ellipse, with the major axis being the centerline and the minor axis being the base of the nose cone. A rotation of a full ellipse about its major axis is called a prolate spheroid, so an elliptical nose shape would properly be known as a prolate hemispheroid. This shape is popular in subsonic flight (such as model rocketry) due to the blunt nose and tangent base.^{[ further explanation needed ]} This is not a shape normally found in professional rocketry, which almost always flies at much higher velocities where other designs are more suitable. If $R$ equals $L$ , this is a hemisphere.

y=R{\sqrt {1-{x^{2} \over L^{2}}}}

Parabolic

Half (

K' = 1/2

)

Three-Quarter (

K' = 3/4

)

Full (

K' = 1

)

Renders of common parabolic nose cone shapes.

This nose shape is not the blunt shape that is envisioned when people commonly refer to a "parabolic" nose cone. The parabolic series nose shape is generated by rotating a segment of a parabola around a line parallel to its latus rectum. This construction is similar to that of the tangent ogive, except that a parabola is the defining shape rather than a circle. Just as it does on an ogive, this construction produces a nose shape with a sharp tip. For the blunt shape typically associated with a parabolic nose, see power series below. (The parabolic shape is also often confused with the elliptical shape.)

For $0\leq K'\leq 1$ : $y=R\left({2\left({x \over L}\right)-K'\left({x \over L}\right)^{2} \over 2-K'}\right)$

$K'$ can vary anywhere between $0$ and $1$ , but the most common values used for nose cone shapes are:

Parabola Type	$K'$ Value
Cone	$0$
Half	$1/2$
Three Quarter	$3/4$
Full	$1$

For the case of the full parabola ( $K' = 1$ ) the shape is tangent to the body at its base, and the base is on the axis of the parabola. Values of $K'$ less than $1$ result in a slimmer shape, whose appearance is similar to that of the secant ogive. The shape is no longer tangent at the base, and the base is parallel to, but offset from, the axis of the parabola.

Power series

Half (

n = 1/2

)

Three-Quarter (

n = 3/4

)

The power series includes the shape commonly referred to as a 'parabolic' nose cone, but the shape correctly known as a parabolic nose cone is a member of the parabolic series (described above). The power series shape is characterized by its (usually) blunt tip, and by the fact that its base is not tangent to the body tube. There is always a discontinuity at the joint between nose cone and body that looks distinctly non-aerodynamic. The shape can be modified at the base to smooth out this discontinuity. Both a flat-faced cylinder and a cone are shapes that are members of the power series.

The power series nose shape is generated by rotating the $y = R (x / L) n$ curve about the $x$ -axis for values of $n$ less than $1$ . The factor $n$ controls the bluntness of the shape. For values of $n$ above about $0.7$ , the tip is fairly sharp. As $n$ decreases towards zero, the power series nose shape becomes increasingly blunt.

For

0\leq n\leq 1

:

y=R\left({x \over L}\right)^{n}

Common values of $n$ include:

Power Type	$n$ Value
Cylinder	$0$
Half (Parabola)	$1/2$
Three Quarter	$3/4$
Cone	$1$

Haack series

LD-Haack (Von Kármán) (

C = 0

)

LV-Haack (

C = 1/3

)

Unlike all of the nose cone shapes above, Wolfgang Haack's series shapes are not constructed from geometric figures. The shapes are instead mathematically derived for the purpose of minimizing drag; a related shape with similar derivation being the Sears–Haack body. While the series is a continuous set of shapes determined by the value of $C$ in the equations below, two values of $C$ have particular significance: when $C = 0$ , the notation $LD$ signifies minimum drag for the given length and diameter, and when $C = 1/3$ , $LV$ indicates minimum drag for a given length and volume. The Haack series nose cones are not perfectly tangent to the body at their base except for the case where $C = 2/3$ . However, the discontinuity is usually so slight as to be imperceptible. For $C > 2/3$ , Haack nose cones bulge to a maximum diameter greater than the base diameter. Haack nose tips do not come to a sharp point, but are slightly rounded.

{\begin{aligned}\theta (x)&=\arccos \left(1-{2x \over L}\right)\\y(\theta ,C)&={R \over {\sqrt {\pi }}}{\sqrt {\theta -{\sin(2\theta ) \over 2}+C\sin ^{3}(\theta )}}\end{aligned}}

Special values of $C$ (as described above) include:

Haack Series Type	$C$ Value
LD-Haack (Von Kármán)	$0$
LV-Haack	$1/3$
Tangent	$2/3$

Von Kármán

The Haack series designs giving minimum drag for the given length and diameter, the LD-Haack where $C = 0$ , is commonly called the Von Kármán or Von Kármán ogive .

Aerospike

An aerospike can be used to reduce the forebody pressure acting on supersonic aircraft. The aerospike creates a detached shock ahead of the body, thus reducing the drag acting on the aircraft.

Nose cone drag characteristics

For aircraft and rockets, below Mach .8, the nose pressure drag is essentially zero for all shapes. The major significant factor is friction drag, which is largely dependent upon the wetted area, the surface smoothness of that area, and the presence of any discontinuities in the shape. For example, in strictly subsonic rockets a short, blunt, smooth elliptical shape is usually best. In the transonic region and beyond, where the pressure drag increases dramatically, the effect of nose shape on drag becomes highly significant. The factors influencing the pressure drag are the general shape of the nose cone, its fineness ratio, and its bluffness ratio.^[2]

Influence of the general shape

Many references on nose cone design contain empirical data comparing the drag characteristics of various nose shapes in different flight regimes. The chart shown here seems to be the most comprehensive and useful compilation of data for the flight regime of greatest interest.^[3] This chart generally agrees with more detailed, but less comprehensive data found in other references (most notably the USAF Datcom).

In many nose cone designs, the greatest concern is flight performance in the transonic region from Mach 0.8 to Mach 1.2. Although data are not available for many shapes in the transonic region, the table clearly suggests that either the Von Kármán shape, or power series shape with $n = 1/2$ , would be preferable to the popular conical or ogive shapes, for this purpose.

This observation goes against the often-repeated conventional wisdom that a conical nose is optimum for 'Mach-breaking'. Fighter aircraft are probably good examples of nose shapes optimized for the transonic region, although their nose shapes are often distorted by other considerations of avionics and inlets. For example, an F-16 Fighting Falcon nose appears to be a very close match to a Von Kármán shape.

Influence of the fineness ratio

The ratio of the length of a nose cone compared to its base diameter is known as the fineness ratio . This is sometimes also called the aspect ratio, though that term is usually applied to wings and tails. Fineness ratio is often applied to the entire vehicle, considering the overall length and diameter. The length/diameter relation is also often called the caliber of a nose cone.

At supersonic speeds, the fineness ratio has a significant effect on nose cone wave drag, particularly at low ratios; but there is very little additional gain for ratios increasing beyond 5:1. As the fineness ratio increases, the wetted area, and thus the skin friction component of drag, will also increase. Therefore, the minimum drag fineness ratio is ultimately going to be a trade-off between the decreasing wave drag and increasing friction drag.

Related Research Articles

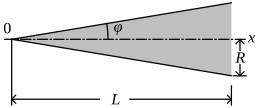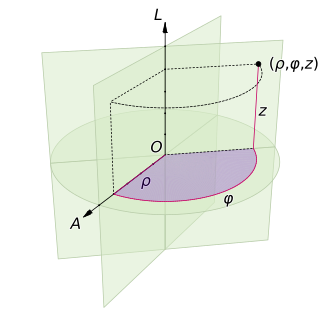
A cylindrical coordinate system is a three-dimensional coordinate system that specifies point positions by the distance from a chosen reference axis (axis L in the image opposite), the direction from the axis relative to a chosen reference direction (axis A), and the distance from a chosen reference plane perpendicular to the axis (plane containing the purple section). The latter distance is given as a positive or negative number depending on which side of the reference plane faces the point.

The Method of Mechanical Theorems, also referred to as The Method, is one of the major surviving works of the ancient Greek polymath Archimedes. The Method takes the form of a letter from Archimedes to Eratosthenes, the chief librarian at the Library of Alexandria, and contains the first attested explicit use of indivisibles. The work was originally thought to be lost, but in 1906 was rediscovered in the celebrated Archimedes Palimpsest. The palimpsest includes Archimedes' account of the "mechanical method", so called because it relies on the center of weights of figures (centroid) and the law of the lever, which were demonstrated by Archimedes in On the Equilibrium of Planes.

In geometry, Descartes' theorem states that for every four kissing, or mutually tangent, circles, the radii of the circles satisfy a certain quadratic equation. By solving this equation, one can construct a fourth circle tangent to three given, mutually tangent circles. The theorem is named after René Descartes, who stated it in 1643.

Orthographic projection in cartography has been used since antiquity. Like the stereographic projection and gnomonic projection, orthographic projection is a perspective projection in which the sphere is projected onto a tangent plane or secant plane. The point of perspective for the orthographic projection is at infinite distance. It depicts a hemisphere of the globe as it appears from outer space, where the horizon is a great circle. The shapes and areas are distorted, particularly near the edges.

Note: This page uses common physics notation for spherical coordinates, in which $is the angle between the z axis and the radius vector connecting the origin to the point in question, while is the angle between the projection of the radius vector onto the x-y plane and the x axis. Several other definitions are in use, and so care must be taken in comparing different sources.$

A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex.

<span class="mw-page-title-main">Cylinder</span> Three-dimensional solid

A cylinder has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base.

<span class="mw-page-title-main">Projectile motion</span> Motion of launched objects due to gravity

Projectile motion is a form of motion experienced by an object or particle that is projected in a gravitational field, such as from Earth's surface, and moves along a curved path under the action of gravity only. In the particular case of projectile motion on Earth, most calculations assume the effects of air resistance are passive and negligible. The curved path of objects in projectile motion was shown by Galileo to be a parabola, but may also be a straight line in the special case when it is thrown directly upward or downward. The study of such motions is called ballistics, and such a trajectory is a ballistic trajectory. The only force of mathematical significance that is actively exerted on the object is gravity, which acts downward, thus imparting to the object a downward acceleration towards the Earth’s center of mass. Because of the object's inertia, no external force is needed to maintain the horizontal velocity component of the object's motion. Taking other forces into account, such as aerodynamic drag or internal propulsion, requires additional analysis. A ballistic missile is a missile only guided during the relatively brief initial powered phase of flight, and whose remaining course is governed by the laws of classical mechanics.

Spirograph is a geometric drawing device that produces mathematical roulette curves of the variety technically known as hypotrochoids and epitrochoids. The well-known toy version was developed by British engineer Denys Fisher and first sold in 1965.

In mathematics, the root test is a criterion for the convergence of an infinite series. It depends on the quantity

The Stokes parameters are a set of values that describe the polarization state of electromagnetic radiation. They were defined by George Gabriel Stokes in 1852, as a mathematically convenient alternative to the more common description of incoherent or partially polarized radiation in terms of its total intensity (I), (fractional) degree of polarization (p), and the shape parameters of the polarization ellipse. The effect of an optical system on the polarization of light can be determined by constructing the Stokes vector for the input light and applying Mueller calculus, to obtain the Stokes vector of the light leaving the system. The original Stokes paper was discovered independently by Francis Perrin in 1942 and by Subrahamanyan Chandrasekhar in 1947, who named it as the Stokes parameters.

In geometry, the area enclosed by a circle of radius $r$ is $π r 2$ . Here the Greek letter $π$ represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.14159.

In fluid dynamics, drag is a force acting opposite to the relative motion of any object moving with respect to a surrounding fluid. This can exist between two fluid layers or between a fluid and a solid surface.

<span class="mw-page-title-main">Multiple integral</span> Generalization of definite integrals to functions of multiple variables

In mathematics (specifically multivariable calculus), a multiple integral is a definite integral of a function of several real variables, for instance, $f (x, y)$ or $f (x, y, z)$ . Physical (natural philosophy) interpretation: S any surface, V any volume, etc.. Incl. variable to time, position, etc.

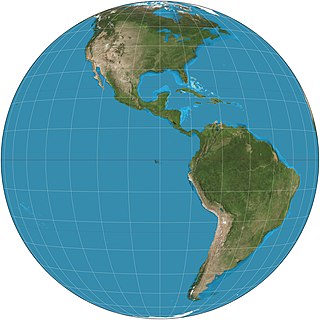
The General Perspective projection is a map projection. When the Earth is photographed from space, the camera records the view as a perspective projection. When the camera is aimed toward the center of the Earth, the resulting projection is called Vertical Perspective. When aimed in other directions, the resulting projection is called a Tilted Perspective.

<span class="mw-page-title-main">Sears–Haack body</span> The most aerodynamic shape for supersonic vehicles

The Sears–Haack body is the shape with the lowest theoretical wave drag in supersonic flow, for a given body length and given volume. The mathematical derivation assumes small-disturbance (linearized) supersonic flow, which is governed by the Prandtl–Glauert equation. The derivation and shape were published independently by two separate researchers: Wolfgang Haack in 1941 and later by William Sears in 1947.

In solid geometry, an ungula is a region of a solid of revolution, cut off by a plane oblique to its base. A common instance is the spherical wedge. The term ungula refers to the hoof of a horse, an anatomical feature that defines a class of mammals called ungulates.

In fluid mechanics, dynamic similarity is the phenomenon that when there are two geometrically similar vessels with the same boundary conditions and the same Reynolds and Womersley numbers, then the fluid flows will be identical. This can be seen from inspection of the underlying Navier-Stokes equation, with geometrically similar bodies, equal Reynolds and Womersley Numbers the functions of velocity (u’,v’,w’) and pressure (P’) for any variation of flow.

<span class="mw-page-title-main">Conical spiral</span> Plane spiral projected onto the surface of a cone

In mathematics, a conical spiral, also known as a conical helix, is a space curve on a right circular cone, whose floor projection is a plane spiral. If the floor projection is a logarithmic spiral, it is called conchospiral.

References

↑ Crowell Sr., Gary A. (1996). The Descriptive Geometry of Nose Cones (PDF) (Report). Archived from the original (PDF) on 11 April 2011. Retrieved 11 April 2011.
↑ Iyer, Aditya Rajan; Pant, Anjali (August 2020). "A Review on Nose Cone Designs for Different Flight Regimes" (PDF). International Research Journal of Engineering and Technology. 7 (8): 3546–3554. S2CID 221684654.
↑ Chin, S. S. (1961). Missile Configuration Design. New York City: McGraw-Hill. LCCN 60-15518. OCLC 253099252.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[crowell-1] Crowell Sr., Gary A. (1996). The Descriptive Geometry of Nose Cones (PDF) (Report). Archived from the original (PDF) on 11 April 2011. Retrieved 11 April 2011.

[irjet-2] Iyer, Aditya Rajan; Pant, Anjali (August 2020). "A Review on Nose Cone Designs for Different Flight Regimes" (PDF). International Research Journal of Engineering and Technology. 7 (8): 3546–3554. S2CID 221684654.

[chinn-3] Chin, S. S. (1961). Missile Configuration Design. New York City: McGraw-Hill. LCCN 60-15518. OCLC 253099252.

[1]

[2]

[3]