In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.

Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Lobachevsky. The simplest examples of smooth spaces are the plane and space curves and surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries.
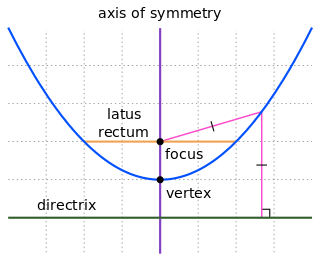
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.

In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is tangent to the curve y = f(x) at a point x = c if the line passes through the point (c, f(c)) on the curve and has slope f'(c), where f' is the derivative of f. A similar definition applies to space curves and curves in n-dimensional Euclidean space.

In mathematics, differential calculus is a subfield of calculus that studies the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus—the study of the area beneath a curve.
In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or surface is contained in a larger space, curvature can be defined extrinsically relative to the ambient space. Curvature of Riemannian manifolds of dimension at least two can be defined intrinsically without reference to a larger space.
In mathematics, two functions have a contact of order k if, at a point P, they have the same value and k equal derivatives. This is an equivalence relation, whose equivalence classes are generally called jets. The point of osculation is also called the double cusp. Contact is a geometric notion; it can be defined algebraically as a valuation.
Differential geometry of curves is the branch of geometry that deals with smooth curves in the plane and the Euclidean space by methods of differential and integral calculus.

In geometry, the Dandelin spheres are one or two spheres that are tangent both to a plane and to a cone that intersects the plane. The intersection of the cone and the plane is a conic section, and the point at which either sphere touches the plane is a focus of the conic section, so the Dandelin spheres are also sometimes called focal spheres.

In the mathematical field of algebraic geometry, a singular point of an algebraic varietyV is a point P that is 'special', in the geometric sense that at this point the tangent space at the variety may not be regularly defined. In case of varieties defined over the reals, this notion generalizes the notion of local non-flatness. A point of an algebraic variety that is not singular is said to be regular. An algebraic variety that has no singular point is said to be non-singular or smooth.

In geometry, focuses or foci are special points with reference to which any of a variety of curves is constructed. For example, one or two foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola. In addition, two foci are used to define the Cassini oval and the Cartesian oval, and more than two foci are used in defining an n-ellipse.

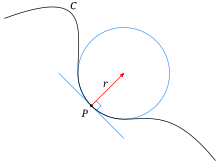
An osculating circle is a circle that best approximates the curvature of a curve at a specific point. It is tangent to the curve at that point and has the same curvature as the curve at that point. The osculating circle provides a way to understand the local behavior of a curve and is commonly used in differential geometry and calculus.

In geometry, Poncelet's closure theorem, also known as Poncelet's porism, states that whenever a polygon is inscribed in one conic section and circumscribes another one, the polygon must be part of an infinite family of polygons that are all inscribed in and circumscribe the same two conics. It is named after French engineer and mathematician Jean-Victor Poncelet, who wrote about it in 1822; however, the triangular case was discovered significantly earlier, in 1746 by William Chapple.

In mathematics, particularly in differential geometry, an osculating plane is a plane in a Euclidean space or affine space which meets a submanifold at a point in such a way as to have a second order of contact at the point. The word osculate is from the Latin osculatus which is a past participle of osculari, meaning to kiss. An osculating plane is thus a plane which "kisses" a submanifold.

The four-vertex theorem of geometry states that the curvature along a simple, closed, smooth plane curve has at least four local extrema. The name of the theorem derives from the convention of calling an extreme point of the curvature function a vertex. This theorem has many generalizations, including a version for space curves where a vertex is defined as a point of vanishing torsion.
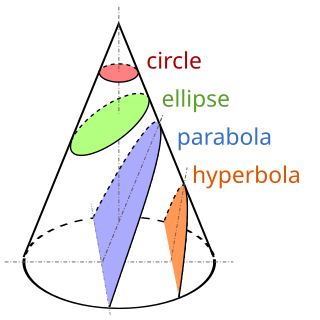
A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though it was sometimes called as a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.
A timeline of calculus and mathematical analysis.

In geometry, a pole and polar are respectively a point and a line that have a unique reciprocal relationship with respect to a given conic section.
The terminology of algebraic geometry changed drastically during the twentieth century, with the introduction of the general methods, initiated by David Hilbert and the Italian school of algebraic geometry in the beginning of the century, and later formalized by André Weil, Jean-Pierre Serre and Alexander Grothendieck. Much of the classical terminology, mainly based on case study, was simply abandoned, with the result that books and papers written before this time can be hard to read. This article lists some of this classical terminology, and describes some of the changes in conventions.