
In geometry, the Pappus configuration is a configuration of nine points and nine lines in the Euclidean plane, with three points per line and three lines through each point. [1]

In geometry, the Pappus configuration is a configuration of nine points and nine lines in the Euclidean plane, with three points per line and three lines through each point. [1]
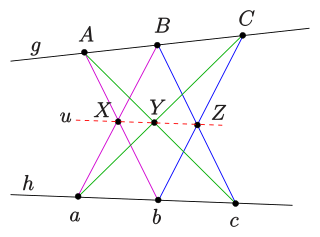
This configuration is named after Pappus of Alexandria. Pappus's hexagon theorem states that every two triples of collinear points ABC and abc (none of which lie on the intersection of the two lines) can be completed to form a Pappus configuration, by adding the six lines Ab, aB, Ac, aC, Bc, and bC, and their three intersection points X = Ab·aB, Y = Ac·aC, and Z = Bc·bC. These three points are the intersection points of the "opposite" sides of the hexagon AbCaBc. According to Pappus' theorem, the resulting system of nine points and eight lines always has a ninth line containing the three intersection points X, Y, and Z, called the Pappus line. [2]

The Pappus configuration can also be derived from two triangles XcC and YbB that are in perspective with each other (the three lines through corresponding pairs of points meet at a single crossing point) in three different ways, together with their three centers of perspectivity Z, a, and A. The points of the configuration are the points of the triangles and centers of perspectivity, and the lines of the configuration are the lines through corresponding pairs of points.

The Levi graph of the Pappus configuration is known as the Pappus graph. It is a bipartite symmetric cubic graph with 18 vertices and 27 edges. [3]
The Desargues configuration can also be defined in terms of perspective triangles, and the Reye configuration can be defined analogously from two tetrahedra that are in perspective with each other in four different ways, forming a desmic system of tetrahedra.
For any nonsingular cubic plane curve in the Euclidean plane, three real inflection points of the curve, and a fourth point on the curve, there is a unique way of completing these four points to form a Pappus configuration in such a way that all nine points lie on the curve. [4]

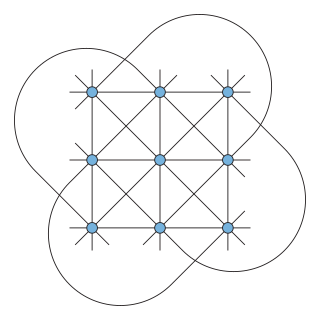
A variant of the Pappus configuration provides a solution to the orchard-planting problem, the problem of finding sets of points that have the largest possible number of lines through three points. The nine points of the Pappus configuration form only nine three-point lines. However, they can be arranged so that there is another three-point line, making a total of ten. This is the maximum possible number of three-point lines through nine points. [5]

In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points to Euclidean points, and vice-versa.

In projective geometry, Desargues's theorem, named after Girard Desargues, states:

In mathematics, a cubic plane curve is a plane algebraic curve C defined by a cubic equation

In projective geometry, Pascal's theorem states that if six arbitrary points are chosen on a conic and joined by line segments in any order to form a hexagon, then the three pairs of opposite sides of the hexagon meet at three points which lie on a straight line, called the Pascal line of the hexagon. It is named after Blaise Pascal.

In geometry an arrangement of lines is the subdivision of the plane formed by a collection of lines. Bounds on the complexity of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.

The Sylvester–Gallai theorem in geometry states that every finite set of points in the Euclidean plane has a line that passes through exactly two of the points or a line that passes through all of them. It is named after James Joseph Sylvester, who posed it as a problem in 1893, and Tibor Gallai, who published one of the first proofs of this theorem in 1944.

In combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for every incidence between a point and a line. They are named for Friedrich Wilhelm Levi, who wrote about them in 1942.
In mathematics, Pappus's hexagon theorem states that
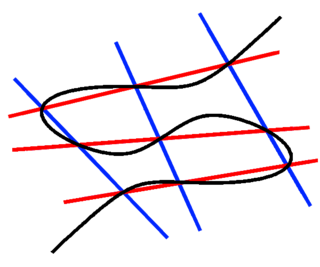
In mathematics, the Cayley–Bacharach theorem is a statement about cubic curves in the projective plane P2. The original form states:
In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear. In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row".

In mathematics, specifically projective geometry, a configuration in the plane consists of a finite set of points, and a finite arrangement of lines, such that each point is incident to the same number of lines and each line is incident to the same number of points.

In geometry, the Desargues configuration is a configuration of ten points and ten lines, with three points per line and three lines per point. It is named after Girard Desargues, and closely related to Desargues' theorem, which proves the existence of the configuration.

Two figures in a plane are perspective from a pointO if the lines joining corresponding points of the figures all meet at O. Dually, the figures are said to be perspective from a line if the points of intersection of corresponding lines all lie on one line. The proper setting for this concept is in projective geometry where there will be no special cases due to parallel lines since all lines meet. Although stated here for figures in a plane, the concept is easily extended to higher dimensions.

In mathematics, a conic section is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.
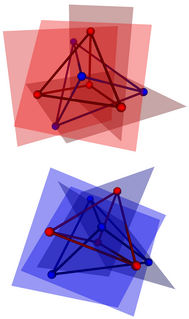
In geometry, the Möbius configuration or Möbius tetrads is a certain configuration in Euclidean space or projective space, consisting of two mutually inscribed tetrahedra: each vertex of one tetrahedron lies on a face plane of the other tetrahedron and vice versa. Thus, for the resulting system of eight points and eight planes, each point lies on four planes, and each plane contains four points.
In geometry, the Hesse configuration, introduced by Colin Maclaurin and studied by Hesse (1844), is a configuration of 9 points and 12 lines with three points per line and four lines through each point. It can be realized in the complex projective plane as the set of inflection points of an elliptic curve, but it has no realization in the Euclidean plane.
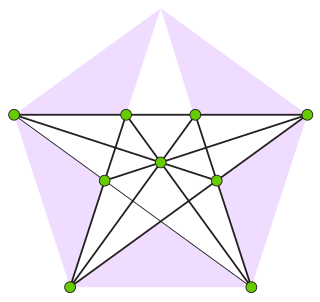
In geometry, the Perles configuration is a system of nine points and nine lines in the Euclidean plane for which every combinatorially equivalent realization has at least one irrational number as one of its coordinates. It can be constructed from the diagonals and symmetry lines of a regular pentagon, omitting one of the symmetry lines. In turn, it can be used to construct higher-dimensional convex polytopes that cannot be given rational coordinates, having the fewest vertices of any known example. All of the realizations of the Perles configuration in the projective plane are equivalent to each other under projective transformations.

In geometry, the Reye configuration, introduced by Theodor Reye (1882), is a configuration of 12 points and 16 lines. Each point of the configuration belongs to four lines, and each line contains three points. Therefore, in the notation of configurations, the Reye configuration is written as 124163.

In geometry, the Grünbaum–Rigby configuration is a symmetric configuration consisting of 21 points and 21 lines, with four points on each line and four lines through each point. Originally studied by Felix Klein in the complex projective plane in connection with the Klein quartic, it was first realized in the Euclidean plane by Branko Grünbaum and John F. Rigby.

In mathematics, modern triangle geometry, or new triangle geometry, is the body of knowledge relating to the properties of a triangle discovered and developed roughly since the beginning of the last quarter of the nineteenth century. Triangles and their properties were the subject of investigation since at least the time of Euclid. In fact, Euclid's Elements contains description of the four special points – centroid, incenter, circumcenter and orthocenter - associated with a triangle. Even though Pascal and Ceva in the seventeenth century, Euler in the eighteenth century and Feuerbach in the nineteenth century and many other mathematicians had made important discoveries regarding the properties of the triangle, it was the publication in 1873 of a paper by Emile Lemoine (1840–1912) with the title "On a remarkable point of the triangle" that was considered to have, according to Nathan Altschiller-Court, "laid the foundations...of the modern geometry of the triangle as a whole." The American Mathematical Monthly, in which much of Lemoine's work is published, declared that "To none of these [geometers] more than Émile-Michel-Hyacinthe Lemoine is due the honor of starting this movement of modern triangle geometry". The publication of this paper caused a remarkable upsurge of interest in investigating the properties of the triangle during the last quarter of the nineteenth century and the early years of the twentieth century. A hundred-page article on triangle geometry in Klein's Encyclopedia of Mathematical Sciences published in 1914 bears witness to this upsurge of interest in triangle geometry.