In physics, a dipole is an electromagnetic phenomenon which occurs in two ways:

Ohm's law states that the electric current through a conductor between two points is directly proportional to the voltage across the two points. Introducing the constant of proportionality, the resistance, one arrives at the three mathematical equations used to describe this relationship:
The quantum Hall effect is a quantized version of the Hall effect which is observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall resistance Rxy exhibits steps that take on the quantized values

In particle physics, bremsstrahlung is electromagnetic radiation produced by the deceleration of a charged particle when deflected by another charged particle, typically an electron by an atomic nucleus. The moving particle loses kinetic energy, which is converted into radiation, thus satisfying the law of conservation of energy. The term is also used to refer to the process of producing the radiation. Bremsstrahlung has a continuous spectrum, which becomes more intense and whose peak intensity shifts toward higher frequencies as the change of the energy of the decelerated particles increases.

The Drude model of electrical conduction was proposed in 1900 by Paul Drude to explain the transport properties of electrons in materials. Basically, Ohm's law was well established and stated that the current J and voltage V driving the current are related to the resistance R of the material. The inverse of the resistance is known as the conductance. When we consider a metal of unit length and unit cross sectional area, the conductance is known as the conductivity, which is the inverse of resistivity. The Drude model attempts to explain the resistivity of a conductor in terms of the scattering of electrons by the relatively immobile ions in the metal that act like obstructions to the flow of electrons.
In differential geometry, the four-gradient is the four-vector analogue of the gradient from vector calculus.
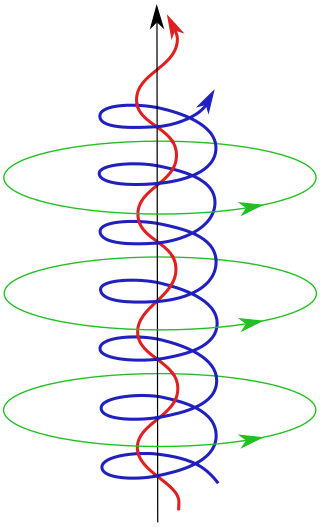
In plasma physics, waves in plasmas are an interconnected set of particles and fields which propagate in a periodically repeating fashion. A plasma is a quasineutral, electrically conductive fluid. In the simplest case, it is composed of electrons and a single species of positive ions, but it may also contain multiple ion species including negative ions as well as neutral particles. Due to its electrical conductivity, a plasma couples to electric and magnetic fields. This complex of particles and fields supports a wide variety of wave phenomena.

An ion trap is a combination of electric and/or magnetic fields used to capture charged particles — known as ions — often in a system isolated from an external environment. Atomic and molecular ion traps have a number of applications in physics and chemistry such as precision mass spectrometry, improved atomic frequency standards, and quantum computing. In comparison to neutral atom traps, ion traps have deeper trapping potentials that do not depend on the internal electronic structure of a trapped ion. This makes ion traps more suitable for the study of light interactions with single atomic systems. The two most popular types of ion traps are the Penning trap, which forms a potential via a combination of static electric and magnetic fields, and the Paul trap which forms a potential via a combination of static and oscillating electric fields.
Radiative transfer is the physical phenomenon of energy transfer in the form of electromagnetic radiation. The propagation of radiation through a medium is affected by absorption, emission, and scattering processes. The equation of radiative transfer describes these interactions mathematically. Equations of radiative transfer have application in a wide variety of subjects including optics, astrophysics, atmospheric science, and remote sensing. Analytic solutions to the radiative transfer equation (RTE) exist for simple cases but for more realistic media, with complex multiple scattering effects, numerical methods are required. The present article is largely focused on the condition of radiative equilibrium.
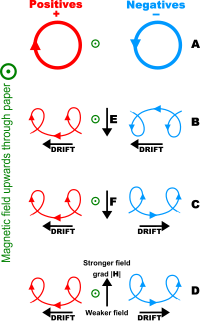
Plasma parameters define various characteristics of a plasma, an electrically conductive collection of charged particles that responds collectively to electromagnetic forces. Plasma typically takes the form of neutral gas-like clouds or charged ion beams, but may also include dust and grains. The behaviour of such particle systems can be studied statistically.
Cyclotron resonance describes the interaction of external forces with charged particles experiencing a magnetic field, thus already moving on a circular path. It is named after the cyclotron, a cyclic particle accelerator that utilizes an oscillating electric field tuned to this resonance to add kinetic energy to charged particles.

In electromagnetism, current density is the amount of charge per unit time that flows through a unit area of a chosen cross section. The current density vector is defined as a vector whose magnitude is the electric current per cross-sectional area at a given point in space, its direction being that of the motion of the positive charges at this point. In SI base units, the electric current density is measured in amperes per square metre.
In quantum mechanics, Landau quantization refers to the quantization of the cyclotron orbits of charged particles in a uniform magnetic field. As a result, the charged particles can only occupy orbits with discrete energy values, called Landau levels. These levels are degenerate, with the number of electrons per level directly proportional to the strength of the applied magnetic field. It is named after the Soviet physicist Lev Landau.
The Appleton–Hartree equation, sometimes also referred to as the Appleton–Lassen equation is a mathematical expression that describes the refractive index for electromagnetic wave propagation in a cold magnetized plasma. The Appleton–Hartree equation was developed independently by several different scientists, including Edward Victor Appleton, Douglas Hartree and German radio physicist H. K. Lassen. Lassen's work, completed two years prior to Appleton and five years prior to Hartree, included a more thorough treatment of collisional plasma; but, published only in German, it has not been widely read in the English speaking world of radio physics. Further, regarding the derivation by Appleton, it was noted in the historical study by Gillmor that Wilhelm Altar first calculated the dispersion relation in 1926.
The electrothermal instability is a magnetohydrodynamic (MHD) instability appearing in magnetized non-thermal plasmas used in MHD converters. It was first theoretically discovered in 1962 and experimentally measured into a MHD generator in 1963 by Evgeny Velikhov.
"This paper shows that it is possible to assert sufficiently specifically that the ionization instability is the number one problem for the utilization of a plasma with hot electrons."
Static force fields are fields, such as a simple electric, magnetic or gravitational fields, that exist without excitations. The most common approximation method that physicists use for scattering calculations can be interpreted as static forces arising from the interactions between two bodies mediated by virtual particles, particles that exist for only a short time determined by the uncertainty principle. The virtual particles, also known as force carriers, are bosons, with different bosons associated with each force.
The Elliott formula describes analytically, or with few adjustable parameters such as the dephasing constant, the light absorption or emission spectra of solids. It was originally derived by Roger James Elliott to describe linear absorption based on properties of a single electron–hole pair. The analysis can be extended to a many-body investigation with full predictive powers when all parameters are computed microscopically using, e.g., the semiconductor Bloch equations or the semiconductor luminescence equations.
The Farley–Buneman instability, or FB instability, is a microscopic plasma instability named after Donald T. Farley and Oscar Buneman. It is similar to the ionospheric Rayleigh-Taylor instability.
In mathematical physics, the Gordon decomposition of the Dirac current is a splitting of the charge or particle-number current into a part that arises from the motion of the center of mass of the particles and a part that arises from gradients of the spin density. It makes explicit use of the Dirac equation and so it applies only to "on-shell" solutions of the Dirac equation.
Shneider-Miles scattering is the quasi-elastic scattering of electromagnetic radiation by charged particles in a small-scale medium with frequent particle collisions. Collisional scattering typically occurs in coherent microwave scattering of high neutral density, low ionization degree microplasmas such as atmospheric pressure laser-induced plasmas. Shneider-Miles scattering is characterized by a 90° phase shift between the incident and scattered waves and a scattering cross section proportional to the square of the incident driving frequency. Scattered waves are emitted in a short dipole radiation pattern. The variable phase shift present in semi-collisional scattering regimes allows for determination of a plasma's collisional frequency through coherent microwave scattering.