In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, certain notable ones can arise through truncation operations on regular simple and star polygons.

In geometry of 4 dimensions or higher, a double prism or duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an n-polytope and an m-polytope is an (n+m)-polytope, where n and m are dimensions of 2 (polygon) or higher.

In geometry, the hexagonal antiprism is the 4th in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.

In geometry, the great dodecahedron is a Kepler–Poinsot polyhedron, with Schläfli symbol {5,5/2} and Coxeter–Dynkin diagram of . It is one of four nonconvex regular polyhedra. It is composed of 12 pentagonal faces, intersecting each other making a pentagrammic path, with five pentagons meeting at each vertex.
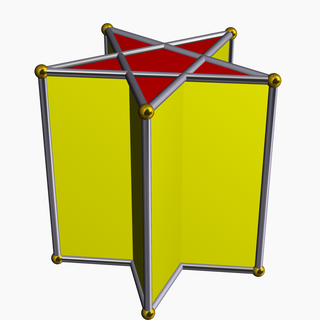
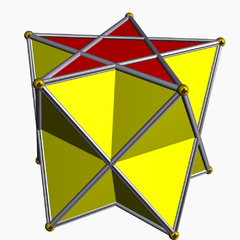
In geometry, the pentagrammic prism is one of an infinite set of nonconvex prisms formed by square sides and two regular star polygon caps, in this case two pentagrams.

In geometry, the small stellated dodecahedron is a Kepler-Poinsot polyhedron, named by Arthur Cayley, and with Schläfli symbol {5⁄2,5}. It is one of four nonconvex regular polyhedra. It is composed of 12 pentagrammic faces, with five pentagrams meeting at each vertex.

In geometry, the great stellated dodecahedron is a Kepler–Poinsot polyhedron, with Schläfli symbol {5⁄2,3}. It is one of four nonconvex regular polyhedra.

In geometry, the great icosahedron is one of four Kepler–Poinsot polyhedra, with Schläfli symbol {3,5⁄2} and Coxeter-Dynkin diagram of . It is composed of 20 intersecting triangular faces, having five triangles meeting at each vertex in a pentagrammic sequence.
In geometry, a snub polyhedron is a polyhedron obtained by performing a snub operation: alternating a corresponding omnitruncated or truncated polyhedron, depending on the definition. Some, but not all, authors include antiprisms as snub polyhedra, as they are obtained by this construction from a degenerate "polyhedron" with only two faces.

In geometry, the pentagrammic crossed-antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams.
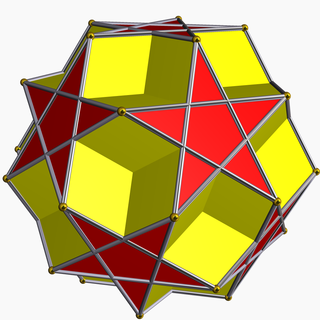
In geometry, the dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U36. It is the rectification of the great dodecahedron (and that of its dual, the small stellated dodecahedron). It was discovered independently by Hess (1878), Badoureau (1881) and Pitsch (1882).

In geometry, the ditrigonal dodecadodecahedron (or ditrigonary dodecadodecahedron) is a nonconvex uniform polyhedron, indexed as U41. It has 24 faces (12 pentagons and 12 pentagrams), 60 edges, and 20 vertices. It has extended Schläfli symbol b{5,5⁄2}, as a blended great dodecahedron, and Coxeter diagram . It has 4 Schwarz triangle equivalent constructions, for example Wythoff symbol 3 | 5⁄3 5, and Coxeter diagram .
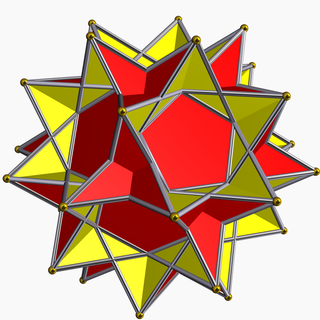
In geometry, the great dodecahemidodecahedron is a nonconvex uniform polyhedron, indexed as U70. It has 18 faces (12 pentagrams and 6 decagrams), 60 edges, and 30 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the small dodecahemicosahedron (or great dodecahemiicosahedron) is a nonconvex uniform polyhedron, indexed as U62. It has 22 faces (12 pentagrams and 10 hexagons), 60 edges, and 30 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the icosidodecadodecahedron (or icosified dodecadodecahedron) is a nonconvex uniform polyhedron, indexed as U44. It has 44 faces (12 pentagons, 12 pentagrams and 20 hexagons), 120 edges and 60 vertices. Its vertex figure is a crossed quadrilateral.

In geometry, the great snub dodecicosidodecahedron (or great snub dodekicosidodecahedron) is a nonconvex uniform polyhedron, indexed as U64. It has 104 faces (80 triangles and 24 pentagrams), 180 edges, and 60 vertices. It has Coxeter diagram . It has the unusual feature that its 24 pentagram faces occur in 12 coplanar pairs.
In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.
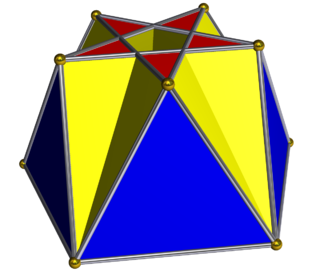
In geometry, the pentagrammic cuploid or pentagrammmic semicupola is the simplest of the infinite family of cuploids. It can be obtained as a slice of the small complex rhombicosidodecahedron. As in all cupolae, the base polygon has twice as many edges and vertices as the top; but in this case the base polygon is a degenerate {10/2} decagram, as the top is a {5/2} pentagram. Hence, the degenerate base is withdrawn and the triangles are connected to the squares instead.