In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.

In graph theory, a component of an undirected graph is a connected subgraph that is not part of any larger connected subgraph. The components of any graph partition its vertices into disjoint sets, and are the induced subgraphs of those sets. A graph that is itself connected has exactly one component, consisting of the whole graph. Components are sometimes called connected components.
In graph theory, a branch of mathematics, the (binary) cycle space of an undirected graph is the set of its even-degree subgraphs.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In the mathematical field of graph theory, a snark is an undirected graph with exactly three edges per vertex whose edges cannot be colored with only three colors. In order to avoid trivial cases, snarks are often restricted to have additional requirements on their connectivity and on the length of their cycles. Infinitely many snarks exist.

In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs: a chordal completion of a graph is typically called a triangulation of that graph.
In the mathematical theory of matroids, a graphic matroid is a matroid whose independent sets are the forests in a given finite undirected graph. The dual matroids of graphic matroids are called co-graphic matroids or bond matroids. A matroid that is both graphic and co-graphic is sometimes called a planar matroid ; these are exactly the graphic matroids formed from planar graphs.

In graph theory, a branch of mathematics, the circuit rank, cyclomatic number, cycle rank, or nullity of an undirected graph is the minimum number of edges that must be removed from the graph to break all its cycles, making it into a tree or forest. It is equal to the number of independent cycles in the graph. Unlike the corresponding feedback arc set problem for directed graphs, the circuit rank r is easily computed using the formula
The arboricity of an undirected graph is the minimum number of forests into which its edges can be partitioned. Equivalently it is the minimum number of spanning forests needed to cover all the edges of the graph. The Nash-Williams theorem provides necessary and sufficient conditions for when a graph is k-arboric.

In the mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.
In graph theory, a connected graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.

In graph theory, a mathematical discipline, a factor-critical graph is a graph with n vertices in which every induced subgraph of n − 1 vertices has a perfect matching.

In graph theory, a cactus is a connected graph in which any two simple cycles have at most one vertex in common. Equivalently, it is a connected graph in which every edge belongs to at most one simple cycle, or in which every block is an edge or a cycle.

In graph theory, a pseudoforest is an undirected graph in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of vertices, such that no two cycles of consecutive edges share any vertex with each other, nor can any two cycles be connected to each other by a path of consecutive edges. A pseudotree is a connected pseudoforest.
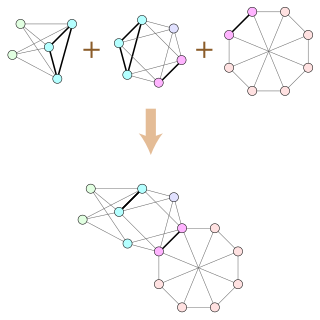
In graph theory, a branch of mathematics, a clique sum is a way of combining two graphs by gluing them together at a clique, analogous to the connected sum operation in topology. If two graphs G and H each contain cliques of equal size, the clique-sum of G and H is formed from their disjoint union by identifying pairs of vertices in these two cliques to form a single shared clique, and then deleting all the clique edges or possibly deleting some of the clique edges. A k-clique-sum is a clique-sum in which both cliques have exactly k vertices. One may also form clique-sums and k-clique-sums of more than two graphs, by repeated application of the clique-sum operation.

In graph theory, Grinberg's theorem is a necessary condition for a planar graph to contain a Hamiltonian cycle, based on the lengths of its face cycles. If a graph does not meet this condition, it is not Hamiltonian. The result has been widely used to prove that certain planar graphs constructed to have additional properties are not Hamiltonian; for instance it can prove non-Hamiltonicity of some counterexamples to Tait's conjecture that cubic polyhedral graphs are Hamiltonian.

In graph theory, a branch of mathematics, a cycle basis of an undirected graph is a set of simple cycles that forms a basis of the cycle space of the graph. That is, it is a minimal set of cycles that allows every even-degree subgraph to be expressed as a symmetric difference of basis cycles.

In graph theory, an ear of an undirected graph G is a path P where the two endpoints of the path may coincide, but where otherwise no repetition of edges or vertices is allowed, so every internal vertex of P has degree two in G. An ear decomposition of an undirected graph G is a partition of its set of edges into a sequence of ears, such that the one or two endpoints of each ear belong to earlier ears in the sequence and such that the internal vertices of each ear do not belong to any earlier ear. Additionally, in most cases the first ear in the sequence must be a cycle. An open ear decomposition or a proper ear decomposition is an ear decomposition in which the two endpoints of each ear after the first are distinct from each other.
In graph theory and graph drawing, a subhamiltonian graph is a subgraph of a planar Hamiltonian graph.
In combinatorial optimization, the matroid parity problem is a problem of finding the largest independent set of paired elements in a matroid. The problem was formulated by Lawler (1976) as a common generalization of graph matching and matroid intersection. It is also known as polymatroid matching, or the matchoid problem.





















